Denominatore di una progressione geometrica: formule e proprietà

La progressione geometrica, insieme all'aritmetica, è un'importante serie numerica, che viene studiata nel corso di algebra della scuola elementare. In questo articolo, consideriamo il denominatore di una progressione geometrica e in che modo il suo valore influenza le sue proprietà.

Definizione di una progressione di geometrica

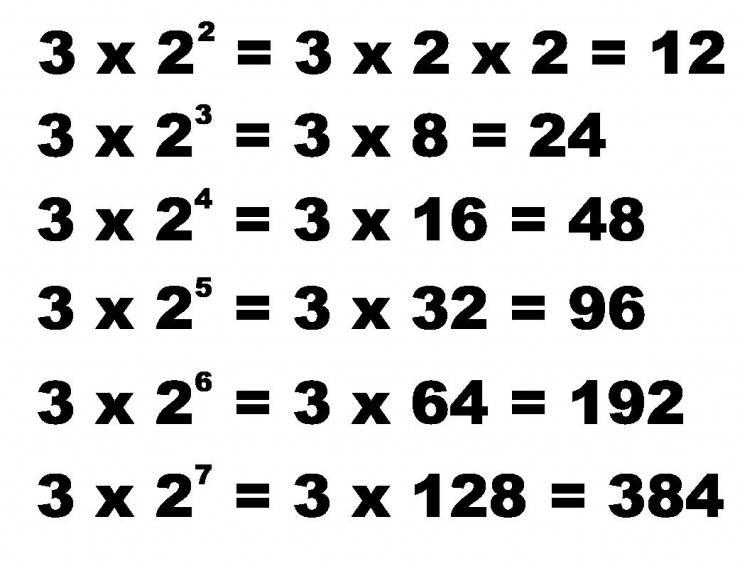
Per cominciare, diamo la definizione di questa serie di numeri. Una tale serie di numeri razionali, che si forma moltiplicando successivamente il suo primo elemento per un numero costante, chiamato denominatore, è chiamata progressione geometrica.

Ad esempio, i numeri nella riga 3, 6, 12, 24, ... sono una progressione geometrica, perché se moltiplichiamo 3 (il primo elemento) per 2, otteniamo 6. Se 6 è moltiplicato per 2, otteniamo 12 e così via.

I membri della sequenza considerata sono solitamente indicati con il simbolo a _i , dove i è un numero intero che indica il numero dell'elemento nella serie.

La suddetta definizione di progressione può essere scritta nel linguaggio della matematica come segue: a _n = b ^n-1 * a ₁ , dove b è il denominatore. È facile controllare questa formula: se n = 1, quindi b ^1-1 = 1, e otteniamo un ₁ = a _1. Se n = 2, quindi a _n = b * a ₁ , e arriviamo nuovamente alla definizione della serie di numeri considerati . Argomenti simili possono essere continuati per grandi valori di n.

Il denominatore della progressione del geometrico

Il numero b determina completamente la natura dell'intera serie di numeri. Il denominatore b può essere positivo, negativo e avere anche un valore maggiore di uno o meno. Tutte queste opzioni portano a sequenze diverse:

• b> 1. C'è un numero crescente di numeri razionali. Ad esempio, 1, 2, 4, 8, ... Se l'elemento a ₁ è negativo, l'intera sequenza aumenterà solo in valore assoluto, ma diminuirà rispetto al segno dei numeri.
• b <-1. In questo caso, stiamo parlando di una serie variabile, vale a dire che gli elementi vicini differiscono nel segno. Ad esempio, 1, -2, 4, -8, 16, ...
• -1 <b <1. Questo è un caso speciale che ha il suo nome - una progressione geometrica infinita decrescente. La sua caratteristica principale è che, indipendentemente dal segno del denominatore, tende ad una somma finita quando si aggiunge un numero infinito di elementi.
• b = 1. Spesso un caso del genere non è chiamato progressione, poiché esiste la solita serie di numeri razionali identici. Ad esempio, -4, -4, -4.

Formula per la somma

Prima di procedere alla considerazione di compiti specifici usando il denominatore del tipo di progressione in questione, dovrebbe essere fornita una formula importante per la somma dei suoi primi n elementi. La formula ha la forma: S _n = (b ⁿ - 1) * a ₁ / (b - 1).

È possibile ottenere questa espressione da soli se si considera una sequenza ricorsiva di membri di una progressione. Si noti inoltre che nella formula sopra, è sufficiente conoscere solo il primo elemento e il denominatore per trovare la somma di un numero arbitrario di membri.

Sequenza infinitamente decrescente

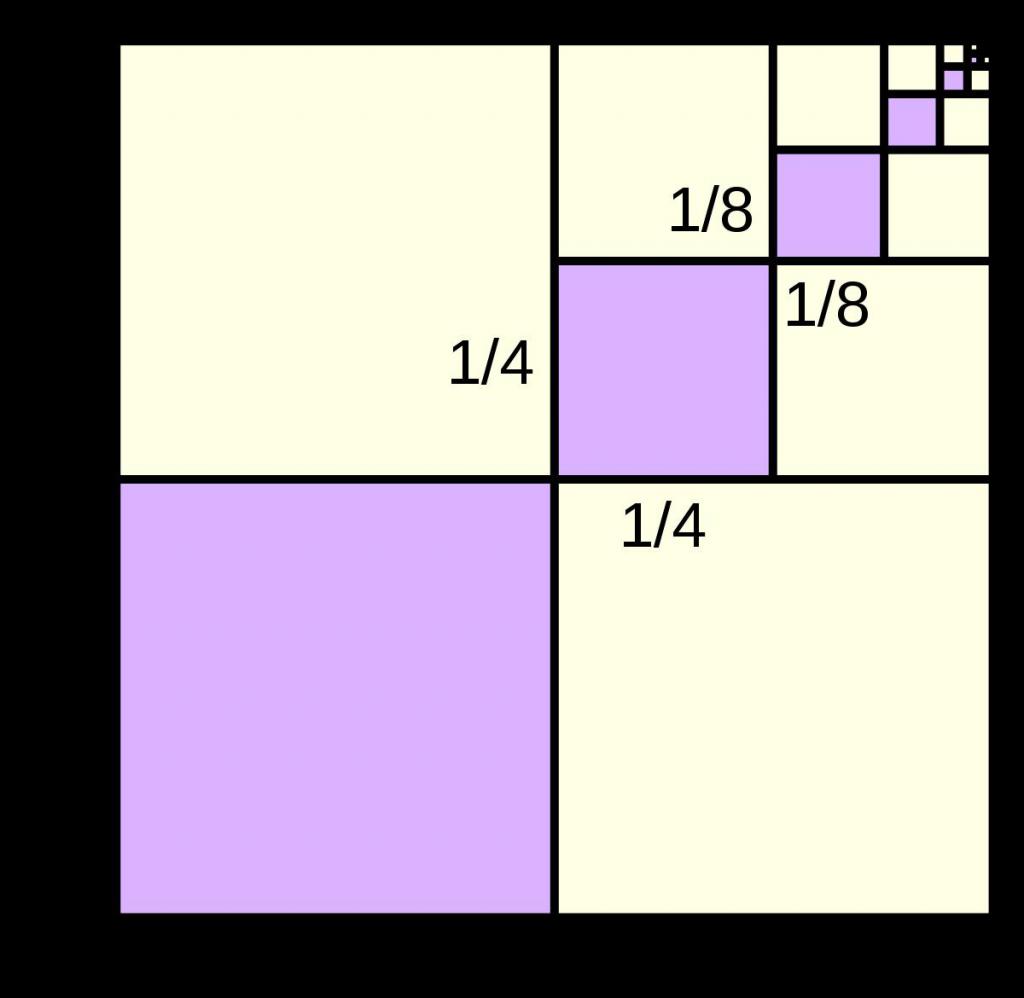
Sopra è stata data una spiegazione di ciò che è. Ora, conoscendo la formula per S _n , applicala a questa serie di numeri. Poiché qualsiasi numero il cui modulo non superi 1, tende a zero quando viene eretto a grandi gradi, cioè b ^∞ => 0, se -1 <b <1 (| b | <1), quindi la formula generale per la somma viene convertita in la seguente espressione: S _∞ = a ₁ / (1 - b).

Poiché la differenza (1 - b) sarà sempre positiva, indipendentemente dal valore del denominatore, il segno della somma di una progressione infinita decrescente della S geometrica S _è determinato unicamente dal segno del suo primo elemento a ₁ .

Ora considereremo diversi compiti, in cui mostreremo come applicare le conoscenze acquisite su numeri concreti.

Problema numero 1. Calcolo degli elementi sconosciuti della progressione e della quantità

Data la progressione del geometrico, il denominatore della progressione 2, e il suo primo elemento 3. A che cosa saranno eguali i suoi membri 7 e 10 e qual è la somma dei suoi sette elementi iniziali?

La condizione del problema è abbastanza semplice e comporta l'uso diretto delle formule di cui sopra. Quindi, per calcolare l'elemento con il numero n, usiamo l'espressione a _n = b ^n-1 * a ₁ . Per il settimo elemento abbiamo: a ₇ = b ⁶ * a _1, sostituendo i dati conosciuti, otteniamo: a ₇ = 2 ⁶ * 3 = 192. Procediamo allo stesso modo per il 10 ° membro: a ₁₀ = 2 ⁹ * 3 = 1536 .

Usiamo la formula nota per la somma e determiniamo questo valore per i primi 7 elementi della serie. Abbiamo: S ₇ = (2 ⁷ - 1) * 3 / (2 - 1) = 381.

Problema numero 2. Determinazione della somma di elementi arbitrari della progressione

Sia -2 uguale al denominatore della progressione nella progressione geometrica b ^n-1 * 4, dove n è un numero intero. È necessario determinare l'importo dal 5 ° al 10 ° elemento di questa serie incluso.

Il problema posto non può essere risolto direttamente usando le formule conosciute. Può essere risolto con 2 metodi diversi. Per completezza, daremo entrambi.

Metodo 1. La sua idea è semplice: è necessario calcolare le due quantità corrispondenti dei primi membri e quindi sottrarre l'una dall'altra. Calcoliamo la somma più piccola: S ₁₀ = ((-2) ¹⁰ - 1) * 4 / (-2 - 1) = -1364. Ora calcoliamo una grande quantità: S ₄ = ((-2) ⁴ - 1) * 4 / (-2 - 1) = -20. Si noti che nell'ultima espressione sono stati riassunti solo 4 termini, poiché il quinto è già incluso nella somma che deve essere calcolata dalla condizione del problema. Infine, fai la differenza: S ₅ ¹⁰ = S ₁₀ - S ₄ = -1364 - (-20) = -1344.

Metodo 2. Prima di sostituire i numeri e contare, è possibile ottenere una formula per la somma tra i membri m e n della serie in esame. Agiamo esattamente nello stesso modo del metodo 1, lavorando solo per primi con la rappresentazione simbolica della somma. Abbiamo: S ⁿ _m = (b ⁿ - 1) * a ₁ / (b - 1) - (b ^m-1 - 1) * a ₁ / (b - 1) = a ₁ * (b ⁿ - b ^{m- 1} ) / (b - 1). È possibile sostituire i numeri noti nell'espressione risultante e calcolare il risultato finale: S ¹⁰ ₅ = 4 * ((-2) ¹⁰ - (-2) ⁴ ) / (-2 - 1) = -1344.

Problema numero 3. Qual è il denominatore?

Sia un ₁ = 2, trova il denominatore della progressione del geometrico, a condizione che la sua somma infinita sia 3, ed è noto che questa è una serie decrescente di numeri.

Dalla condizione del problema non è difficile indovinare quale formula dovrebbe essere utilizzata per risolverlo. Naturalmente, dato che la somma della progressione sta diminuendo all'infinito. Abbiamo: S _∞ = a ₁ / (1 - b). Da dove esprimiamo il denominatore: b = 1 - a ₁ / S _∞ . Resta da sostituire i valori noti e ottenere il numero richiesto: b = 1 - 2/3 = -1 / 3 o -0.333 (3). È possibile controllare qualitativamente questo risultato se ricordiamo che per questo tipo di sequenza il modulo b non deve andare oltre 1. Come si può vedere, | -1 / 3 | <1.

Problema numero 4. Recupero di una serie di numeri

Diamo 2 elementi di una serie numerica, ad esempio, il 5 ° è 30 e il 10 è 60. È necessario ricostruire l'intera serie da questi dati, sapendo che soddisfa le proprietà di una progressione geometrica.

Per risolvere il problema, è necessario iniziare a scrivere l'espressione corrispondente per ogni membro conosciuto. Abbiamo: a ₅ = b ⁴ * a ₁ e a ₁₀ = b ⁹ * a ₁ . Ora dividiamo la seconda espressione nella prima, otteniamo: a ₁₀ / a ₅ = b ⁹ * a ₁ / (b ⁴ * a ₁ ) = b ⁵ . Quindi, determiniamo il denominatore, prendendo la radice di quinto grado dal rapporto tra i termini noti dalla condizione del problema, b = 1.148698. Il numero risultante è sostituito in una delle espressioni per un elemento conosciuto, otteniamo: a ₁ = a ₅ / b ⁴ = 30 / (1,148698) ⁴ = 17.2304966.

Quindi, abbiamo trovato a che cosa è uguale il denominatore della progressione bn e la progressione geometrica b ^n-1 * 17,2304966 = a _n , dove b = 1,148698.

Dove viene applicata la progressione geometrica?

Se in pratica non vi fosse alcuna applicazione di questa serie numerica, il suo studio sarebbe ridotto a un interesse puramente teorico. Ma una tale applicazione esiste.

I seguenti sono i 3 esempi più famosi:

• Il paradosso di Zenone, in cui l'abile Achille non riesce a raggiungere la tartaruga lenta, viene risolto usando il concetto di una sequenza infinita di numeri infinita.
• Se metti chicchi di grano su ogni cella di una scacchiera, metti 1 grano sulla 1a cella, 2 sul 2o, 2 sul 3o e così via, quindi hai bisogno di 18446744073709551615 grani per riempire tutte le celle della scacchiera!
• Nel gioco "Torre di Hanoi", per riorganizzare i dischi da un'asta all'altra, è necessario eseguire 2 operazioni ⁿ -1, ovvero il loro numero cresce esponenzialmente con il numero di dischi usati n.