Determinazione del momento angolare, della forza e dell'inerzia. Equazione del momento Un esempio di risoluzione del problema
La dinamica della rotazione è una delle sezioni importanti della meccanica moderna, che considera le leggi del movimento rotatorio dei corpi attorno ad assi e punti. In questo articolo studieremo in dettaglio l'equazione principale delle dinamiche di rotazione: l'equazione dei momenti.
Momento di impulso
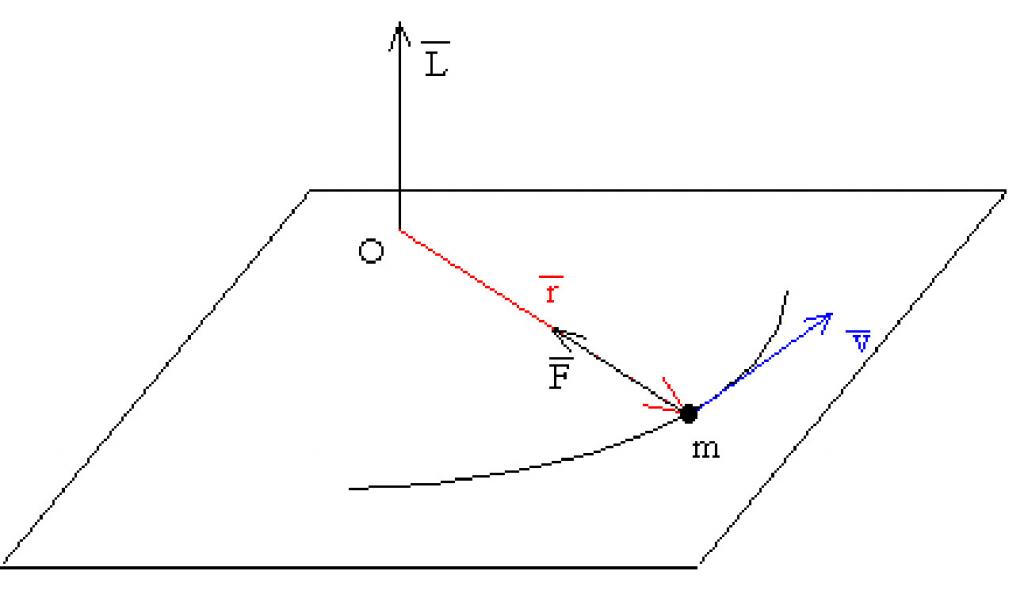
Ogni scolaro sa cosa costituisce un impulso meccanico, che è più correttamente chiamato la quantità di movimento. Supponiamo ora che un punto materiale avente massa m ruoti attorno all'asse O con una velocità lineare v. Se il raggio di rotazione è designato come r, allora possiamo scrivere la seguente espressione:
L¯ = [m * v¯ * r¯].
I primi due fattori sul lato destro dell'uguaglianza sono il momento lineare di un punto. Il prodotto di questo impulso dal vettore r, diretto dall'asse di rotazione a un punto, è chiamato il momento angolare L¯.
Ad
Il valore di L¯ è vettoriale. È diretto perpendicolare al piano di rotazione di un punto. La direzione del momento angolare del punto materiale è determinata usando la regola della mano destra o la regola del succhiello. Ruotando il punto in senso antiorario si crea un momento angolare positivo.
Poiché la velocità di rotazione v è diretta tangenzialmente ad un percorso circolare, l'espressione vettoriale può essere riscritta in forma scalare:
L = m * v * r.
Momento di forza
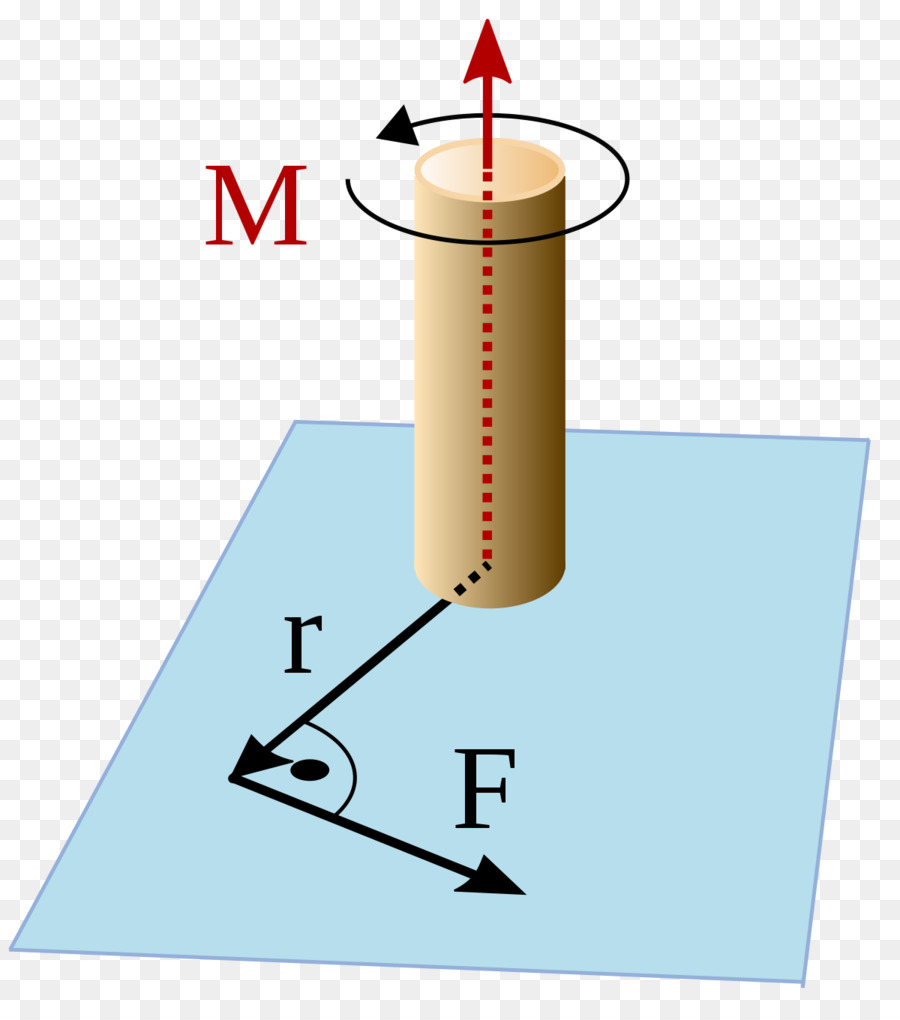
Questa è un'altra importante caratteristica del movimento rotazionale. In fisica, questa quantità viene introdotta allo stesso modo del momento angolare di un punto materiale, ma invece della quantità di movimento, si dovrebbe sostituire la forza tangenziale con la formula scritta sopra. Abbiamo:
M¯ = [r¯ * F¯].
Il momento di forza, che è anche chiamato momento di coppia, caratterizza la capacità di quest'ultimo di fare una svolta del sistema e dargli accelerazione angolare.
La direzione del vettore di coppia M¯ è determinata dalle stesse regole del vettore L¯. Se il sistema esegue una rotazione accelerata, allora M¯ e L¯ coincidono in direzione, se rallentate, allora saranno dirette in senso opposto.
Ad
Se la forza F ¯ e il vettore del raggio r будут sono reciprocamente perpendicolari, allora la forma vettoriale del record si trasformerà in uno scalare simile:
M = r * F.
Il valore di r è chiamato la leva della forza. Maggiore è il suo valore, maggiore è il momento in cui la forza F crea, e maggiore sarà l'accelerazione angolare del sistema.
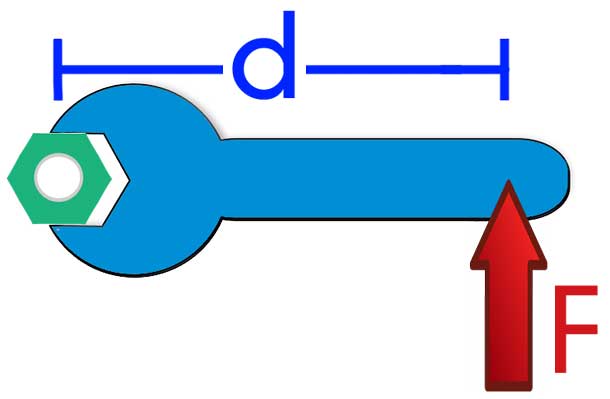
Esempi che consentirebbero un'idea più chiara di quale sia il significato fisico di M¯, stanno svitando il dado con una chiave lunga speciale, il processo di apertura della porta con la sua spinta vicino al manico e vicino ai cardini della porta, così come il processo di trattenere il corpo di una certa massa allungato e premuto sul corpo mano.
Momento di inerzia
Resta da definire il terzo punto, che è usato per descrivere quantitativamente il processo di rotazione. Il momento di inerzia del punto materiale, i cui parametri sono stati registrati all'inizio dell'articolo, è calcolato dalla formula:
I = m * r 2 .
A differenza degli altri due momenti (M¯ e L¯), il momento di inerzia è uno scalare. Con l'aiuto di esso, vengono descritte le proprietà inerziali del sistema (analogia con la massa durante il movimento traslatorio).
Ovviamente, per determinare il valore di I per un corpo solido di forma complessa e densità non uniforme, è necessario utilizzare il numero integrale:
I = ∫ m (r 2 * dm).
In effetti, la formula riflette la somma delle quantità I i per ogni punto materiale i.
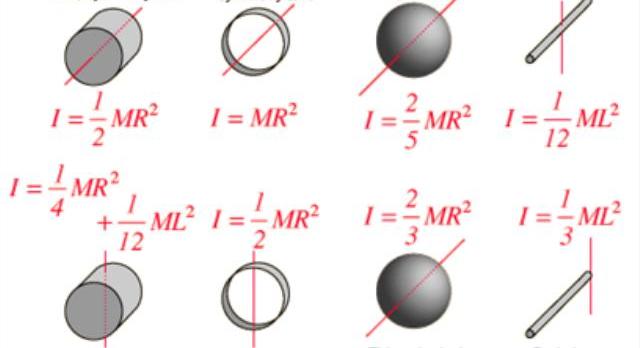
Il momento di inerzia I è caratteristico non solo della forma e della distribuzione della massa nel sistema di rotazione, ma dipende anche dalla posizione dell'asse. Ad esempio, molti hanno notato che è molto più facile ruotare un'asta di metallo o una scopa di legno lungo un asse che percorre la loro lunghezza piuttosto che lungo un asse perpendicolare. Nel secondo caso, il momento di inerzia assume un significato maggiore.
Ad
Equazione del momento per punto materiale
Ora è il momento di andare direttamente all'argomento dell'articolo. Se la coppia M agisce per un tempo dt, allora porta ad una variazione del momento angolare di una quantità dL, cioè:
dL = M * dt.
Questa uguaglianza è una forma differenziale di scrivere l'equazione del momento in fisica. Trasferisci il termine dt sul lato sinistro dell'eguaglianza e riscrivi dL esplicitamente, otteniamo:
dL / dt = M =>
m * dv * r / dt = M.
Ricordiamo che la velocità lineare in cinematica è correlata all'equazione angolare seguente:
v = ω * r.
Sostituendolo nell'equazione dei momenti, otteniamo:
m * dω * r 2 / dt = M =>
I * α = M, dove α = dω / dt, I = m * r 2 .
L'uguaglianza ottenuta viene spesso utilizzata per determinare le caratteristiche cinematiche di un sistema rotante se il momento delle forze esterne M e il momento di inerzia I sono noti.
La legge di conservazione del valore L
L'equazione del momento mostra come cambia il momento angolare se agisce un momento esterno M. Cosa succederà al sistema se M risulta essere zero? In questo caso, il valore di L verrà salvato. La formula matematica per questa situazione è scritta come segue:
Ad
L = const o
L = m * r * v = m * r 2 * ω = I * ω = const.
Si noti che la condizione M = 0 deve essere soddisfatta solo per forze esterne. Le forze interne che creano il momento M non possono cambiare il momento del momento del sistema.
La legge di conservazione L viene utilizzata per ruotare i satelliti artificiali nello spazio esterno e nel pattinaggio artistico. Quindi, raggruppando in vari modi, l'atleta cambia il valore del suo momento d'inerzia, che porta ad un cambiamento proporzionale nella velocità della sua rotazione angolare.

Compito di esempio
Una forza di 10 N agisce su un punto materiale del peso di 2 Kg. Sapendo che il raggio di rotazione di un punto materiale attorno all'asse è di 0,5 m, e considerando anche che la forza agisce in modo tangenziale alla traiettoria, è necessario trovare la velocità angolare del punto 5 secondi dopo l'inizio del movimento .
Scriviamo l'equazione del momento ed esprimiamo l'accelerazione α:
I * α = M =>
α = M / I.
Ora sostituiamo le espressioni per M e I, tenendo conto delle condizioni del problema, abbiamo:
α = F * r / (m * r 2 ) = F / (m * r).
Poiché il movimento in esame si verifica con un'accelerazione costante α, la seguente formula sarà adatta per il calcolo di ω:
ω = α * t.
Sostituendo in esso l'espressione risultante per α, arriviamo alla formula finale di lavoro:
ω = F * t / (m * r).
Dati i dati del problema, puoi scrivere la risposta: ω = 50 rad / s. Questo valore corrisponde a quasi 8 giri completi attorno all'asse al secondo.