Punti funzionali estremi. Come trovare?
Analisi matematica - questa è una sezione di matematica piuttosto divertente, che assolutamente tutti i laureati e gli studenti devono affrontare. Tuttavia, non a tutti piace Matan. Alcuni potrebbero non capire anche le cose elementari come lo studio apparentemente standard di una funzione. Questo articolo ha lo scopo di correggere un tale errore. Vuoi saperne di più sull'analisi della funzione? Volete sapere quali sono i punti estremi e come trovarli? Allora questo articolo è per te.
Studio del grafico della funzione
Prima di tutto, vale la pena capire perché è necessario analizzare il grafico. Ci sono funzioni semplici da disegnare che non sono difficili. La parabola può servire come un vivido esempio di tale funzione. Disegnare il suo programma non è difficile. Tutto ciò che serve è trovare i numeri per i quali la funzione assume un valore usando una semplice trasformazione e, in linea di principio, questo è tutto ciò che è necessario disegnare per disegnare un grafico di una parabola.
Ad
Ma cosa succede se la funzione di cui dobbiamo disegnare il grafico è molto più difficile? Poiché le proprietà di funzioni complesse sono piuttosto oscure, è necessario effettuare un'analisi completa. Solo allora la funzione può essere rappresentata graficamente. Come si fa? La risposta a questa domanda può essere trovata in questo articolo.
Piano di analisi funzionale
La prima cosa che deve essere fatta è condurre uno studio superficiale della funzione, durante la quale troveremo il dominio di definizione. Quindi iniziamo in ordine. Il dominio di definizione è una raccolta dei valori con cui viene specificata la funzione. In parole povere, questi sono i numeri che possono essere usati nella funzione invece di x. Per determinare l'ambito, devi solo guardare la voce. Ad esempio, è ovvio che la funzione y (x) = x 3 + x 2 - x + 43 dominio di definizione è l'insieme di numeri reali. Bene, con una funzione come (x 2 - 2x) / x, tutto è un po 'diverso. Poiché il numero nel denominatore non deve essere 0, il reame della funzione sarà tutti i numeri reali, oltre allo zero.
Ad
Successivamente, è necessario trovare i cosiddetti zero di funzione. Questi sono i valori dell'argomento per i quali l'intera funzione assume valori pari a zero. Per fare ciò, è necessario equiparare la funzione a zero, considerarla in dettaglio ed eseguire alcune trasformazioni. Prendi la funzione y (x) = (x 2 - 2x) / x che ci è già familiare. Dal corso scolastico, sappiamo che la frazione è 0 quando il numeratore è zero. Pertanto, scartiamo il denominatore e iniziamo a lavorare con il numeratore, equiparandolo a zero. Otteniamo x 2 - 2x = 0 e mettiamo x per parentesi. Quindi x (x - 2) = 0. Come risultato, troviamo che la nostra funzione è zero quando x è uguale a 0 o 2.
Punti estremi sul grafico della funzione
Durante lo studio del grafico della funzione, molti affrontano il problema sotto forma di punti estremi. Ed è strano Dopotutto, gli estremi sono un argomento piuttosto semplice. Non crederci? Vedi di persona leggendo questa parte dell'articolo, in cui parleremo dei punti di minimo e massimo.
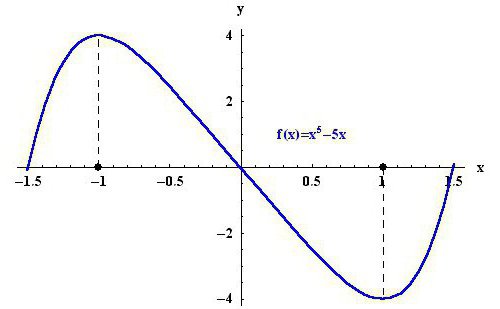
Iniziare è capire cosa costituisce un estremo. L'estremo è il valore limite che la funzione raggiunge sul grafico. Da qui risulta che ci sono due valori estremi: massimo e minimo. Per chiarezza, puoi guardare l'immagine qui sopra. Nell'area studiata, il punto -1 è il massimo della funzione y (x) = x 5 - 5x e il punto 1, rispettivamente, è il minimo.
Ad
Inoltre, non confondere concetti. I punti estremi della funzione sono quegli argomenti a cui la funzione data acquisisce valori estremi. A sua volta, l'estremo è il valore dei minimi e dei massimi della funzione. Ad esempio, considera nuovamente l'immagine sopra. -1 e 1 sono i punti estremi della funzione, e 4 e -4 sono gli stessi estremi.
Trovare punti estremi
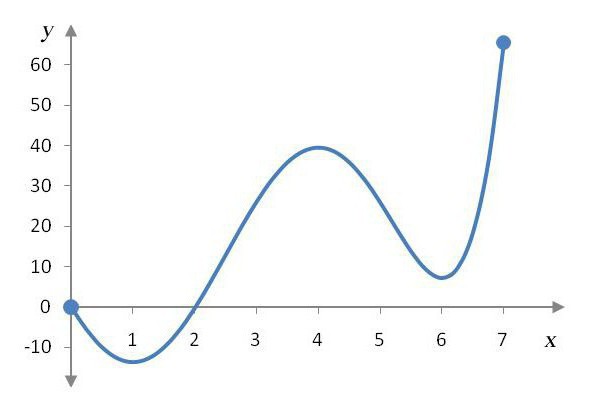
Ma come si possono trovare i punti estremi di una funzione? È piuttosto semplice La prima cosa da fare è trovare la derivata dell'equazione. Supponiamo di avere il compito: "Trova i punti estremi della funzione y (x), x è l'argomento.Per chiarezza, prendiamo la funzione y (x) = x 3 + 2x 2 + x + 54. Distinguiamo e prendiamo la seguente equazione: 3x 2 + 4x + 1. Alla fine, abbiamo ottenuto lo standard equazione quadratica. Tutto ciò che deve essere fatto dopo è di azzerarlo e trovare le radici. Poiché il discriminante è maggiore di zero (D = 16 - 12 = 4), questa equazione è definita da due radici. Trovali e ottieni due valori: 1/3 e -1. Questi saranno i punti estremi della funzione. Tuttavia, come si determina chi è chi? Quale punto è il massimo e qual è il minimo? Per fare ciò, prendi il prossimo punto e scopri il suo valore. Ad esempio, prendi il numero -2, che si trova a sinistra della linea di coordinate da -1. Sostituiamo questo valore nella nostra equazione y (-2) = 12 - 8 + 1 = 5. Di conseguenza, abbiamo ottenuto un numero positivo. Ciò significa che nell'intervallo da 1/3 a -1 la funzione aumenta. Questo, a sua volta, significa che negli intervalli da meno infinito a 1/3 e da -1 a più infinito, la funzione diminuisce. Quindi, possiamo concludere che il numero 1/3 è il punto minimo della funzione sull'intervallo studiato, e -1 è il punto massimo.
La somma dei punti estremi della funzione

Vale anche la pena notare che non è solo necessario trovare punti estremi sull'USO, ma anche eseguire qualche tipo di operazione con loro (aggiungi, moltiplica, ecc.). È per questo motivo che occorre prestare particolare attenzione alle condizioni del problema. Dopotutto, a causa della disattenzione, puoi perdere punti.