Metodo degli elementi finiti e sua applicazione

Il metodo degli elementi finiti è emerso come una delle tecniche per studiare vari progetti. Attualmente, è universalmente riconosciuto come un modo comune per risolvere una vasta gamma di compiti in vari campi della tecnologia.

definizione

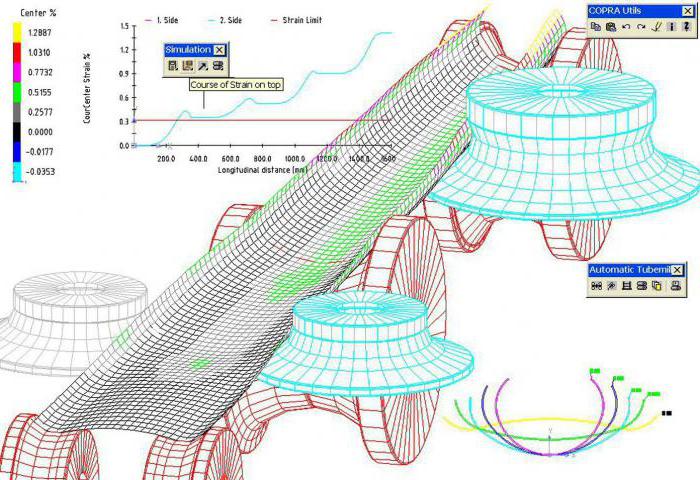
L'analisi ingegneristica mediante il metodo degli elementi finiti consiste nell'approssimazione di un mezzo continuo con un numero infinitamente grande di gradi di libertà da un insieme di elementi (sottodomini) con numeri finiti di gradi di libertà. La relazione tra questi elementi è stabilita. Il riconoscimento del metodo è spiegato dalla semplicità della sua forma matematica e interpretazione fisica.

Utilizzare in meccanica

Il metodo degli elementi finiti nella meccanica della frattura e nei problemi della meccanica strutturale è espresso come il rapporto tra la FEM sotto forma di spostamenti. Innanzitutto, le cosiddette funzioni del modulo sono impostate all'interno di ciascun elemento. Definiscono il movimento nell'area interna dell'elemento dal movimento nei nodi. Questi ultimi sono punti in cui gli elementi finiti sono combinati.

FEM sconosciute sono possibili e movimenti indipendenti di nodi di un modello ad elementi finiti (CEM). Pertanto, la progettazione KEM è un sistema di nodi fissi. Link aggiuntivi correlati alla direzione di possibili movimenti dei nodi.

L'essenza del metodo

Nel suo nucleo, il modello elementare del progetto è simile al sistema di base del metodo classico di spostamento, che viene utilizzato nel calcolo dei sistemi di barre. Per ottenere una precisione ricettiva dei risultati dei calcoli usando il metodo degli elementi finiti, è necessario ridurre la dimensione degli elementi, aumentando così la precisione dell'approssimazione delle caratteristiche geometriche e delle funzioni degli spostamenti all'interno dell'elemento finito.

Le strutture complesse del CEM raggiungono centinaia o addirittura milioni di gradi di libertà, e quindi il metodo degli elementi finiti in ingegneria è orientato alla macchina, la cui implementazione è possibile solo per mezzo di computer.

Implementazione pratica

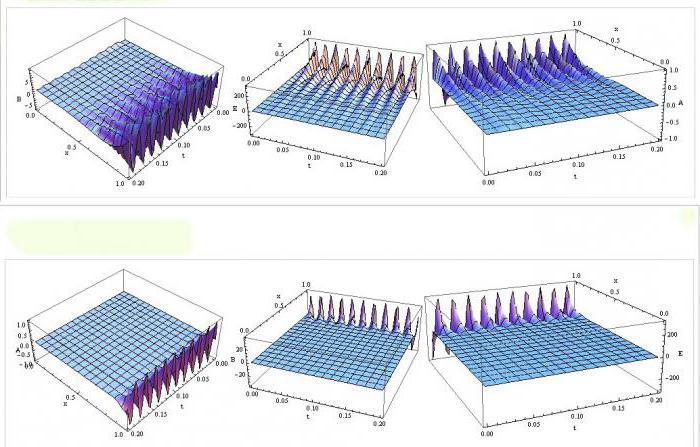
Per applicare la FEM in pratica, è necessario comprendere non solo la teoria della meccanica, ma anche conoscere la programmazione. L'applicazione del metodo degli elementi finiti si basa spesso sui principi variazionali della meccanica, che si basano su due scalari fondamentali: potenziale e energia cinetica costruzione elastica. La definizione di questi scalari, indipendente dal sistema di coordinate scelto, consente di scrivere la relazione FEM in una forma invariante.

Per facilità di programmazione, i rapporti FEM sono registrati in una matrice compatta o forma tensoriale. Allo stato attuale, la simulazione con il metodo degli elementi finiti è completamente provata matematicamente, vengono creati prodotti software ad alte prestazioni, che vengono costantemente migliorati insieme agli strumenti di programmazione.

Programmi educativi

Il progresso tecnico, soprattutto nel campo dei computer, ha modificato in modo significativo le opinioni sulla formulazione e sulla soluzione dei problemi di ingegneria. La costruzione di un modello computazionale è strettamente correlata al processo computazionale ed è quasi impossibile separare queste due fasi sul percorso per ottenere risultati pratici.

Il metodo degli elementi finiti è ampiamente utilizzato nella pratica ingegneristica, che ha anche contribuito alla sua inclusione nei curricula delle università. FEM fornisce modi per costruire un modello matematico del fenomeno preso in considerazione, basato sulla sua essenza fisica.

I primi libri di testo su FEM sono stati scritti in un linguaggio complesso, ma presto i metodi di insegnamento sono stati semplificati grazie all'introduzione di programmi specializzati. Ad esempio, il pacchetto software Assistant ha dato ottimi risultati. Ti permette di testare le conoscenze degli studenti online e contribuisce allo sviluppo di competenze che lavorano con prodotti software nella risoluzione di problemi pratici.

Calcolo delle deformazioni lineari

Oggi, i fondamenti del metodo degli elementi finiti si basano sul fatto che i valori e i concetti intrinseci non vengono introdotti in anticipo, ma seguono dall'essenza del problema della meccanica strutturale. La gamma di problemi che possono essere risolti con l'aiuto del FEM è quasi illimitata. Si consideri ad esempio il problema del calcolo della deformazione lineare delle strutture elastiche dall'azione dei carichi statici.

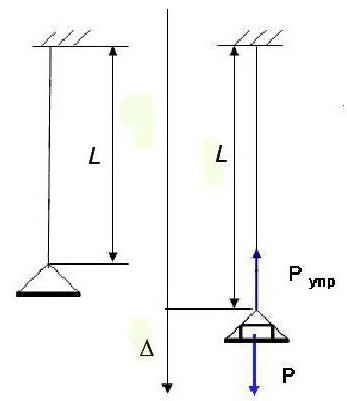
Il fisico inglese R. Hooke ha condotto una ricerca sulle deformazioni delle aste a caricamento centrale fatte di diversi materiali elastici sotto l'azione di una forza statica: Δ = Pl / EA.

Stabilì anche una relazione tra le quantità che determinano questo processo: σ = Eε, dove la deformazione è espressa dalla relazione ε = Δ / l, lo sforzo è designato come σ = P / A (qui A è l'area della sezione trasversale della verga).

Il coefficiente di proporzionalità E determina le caratteristiche elastiche del materiale e ha un'essenza fisica - lo stress corrispondente a un ceppo unitario.

Influenza della forza statica

La forza che agisce staticamente cresce gradualmente nel tempo (G≥P≥0). Anche i movimenti che genera crescono gradualmente, senza accelerazione.

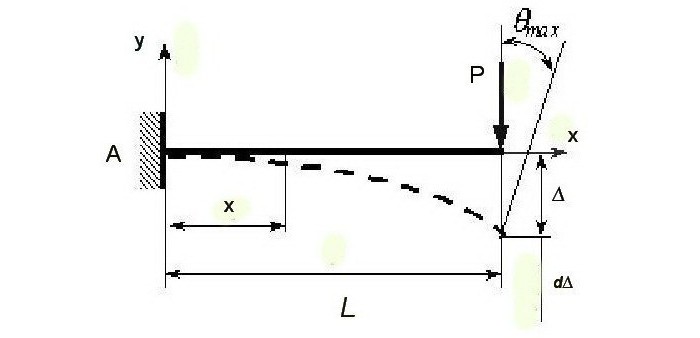
L'analisi mediante il metodo degli elementi finiti ci consente di determinare l'effetto della forza statica sullo spostamento, dato che questi indicatori variano. Un aumento (aumento) in vigore su un valore infinitamente piccolo dP corrisponde ad un aumento (aumento) dello spostamento dΔ. La forza lavoro (P + ΔP) sullo spostamento dΔ è dA = (P + ΔP) × dΔ.

Il valore finale della forza lavoro è determinato dalla formula A = PdΔ.

Introduciamo la relazione tra le variabili dimensionali sotto il segno dell'integrale Δ = Pα, dove α è il coefficiente di conformità, che esprime l'essenza fisica del movimento di un punto, a cui è aggiunta una forza unitaria, nella direzione di questa forza. Il rapporto Δ = Pα imposta l'unità di misura α (m / N). Ne consegue che dΔ = dPα.

Il coefficiente di conformità corrisponde a un'altra importante caratteristica della struttura: il coefficiente di rigidezza k = l / α (n / m), che determina la forza che causa un singolo movimento della struttura nella direzione di questa forza.

Tenendo conto di tutte le caratteristiche e i coefficienti, l'equazione finale assume la forma: A = PdPα = α × (P 2/2) = (GΔ) / 2.

Si ottiene la formula di Clapeyron, che determina il lavoro effettivo di una forza che agisce staticamente sullo spostamento, che essa stessa ha generato in un corpo elastico. Altri metodi numerici sono calcolati usando questa tecnica.

Metodo degli elementi finiti per sistemi a barre

L'asta è un corpo spaziale, due dimensioni di cui larghezza e altezza sono molto meno lunghe della lunghezza. Ciò rende possibile considerare il suo modello fisico sotto forma di una linea che passa attraverso i centri delle sezioni. Se le forze esterne applicate all'asta si trovano nello stesso piano con il suo modello, allora possiamo supporre che le sue deformazioni si verificano nello stesso piano.

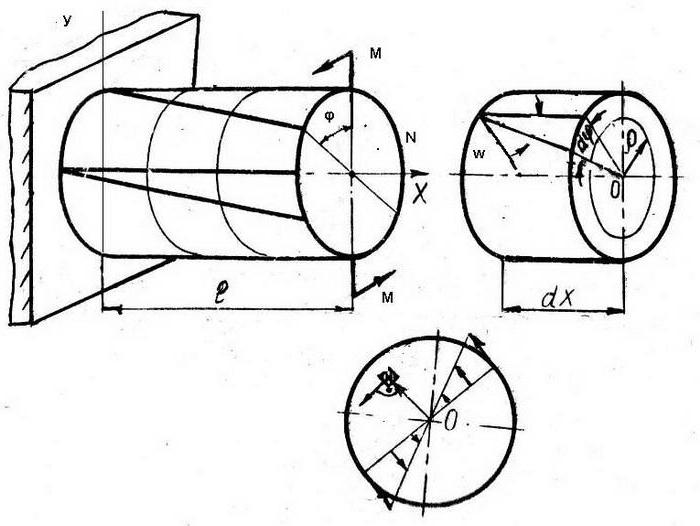
Da un punto di vista matematico, le caratteristiche geometriche dello spostamento e dello stress all'interno di una verga sono funzioni dello stesso argomento. Le relazioni della teoria dell'elasticità si basano sull'ipotesi di sezioni piatte dell'asta. La relazione tra deformazioni e sollecitazioni corrisponde alla legge lineare di Hooke. In ciascuna sezione dell'asta compaiono tre piani di movimento:

• la coordinata u è la forza longitudinale;
• coordinare w - deflessione;
• coordinate φ - angolo di rotazione.

In questo caso, la longitudinale u e la deflessione w sono indipendenti e l'angolo di rotazione è espresso dalla formula φ = dw / dx, dove dw è la quantità di deflessione dopo l'applicazione di una forza esterna all'asta, dx è il segmento di deflessione (determinato dal valore di w + dw).

Per un'asta infinitamente piccola dx, la relazione dx = dφ × P è valida.

Energia potenziale Le deformazioni delle aste sono naturalmente calcolate in un sistema di coordinate locale il cui asse x coincide con l'asse della barra e l'asse y è perpendicolare all'asse della barra: U = ½∫N × du + ½∫M × dφ = ½∫N × (du / dx) dx + ½ ∫ M × (d²w / dx²) dx.

Approccio isoparametrico in FEM

Considerare l'applicazione del metodo degli elementi finiti in un sistema isoparametrico di elementi finiti di una struttura sottoposta a sollecitazione del piano. Il processo di creazione di un modello ad elementi finiti di strutture consiste di diverse fasi, la prima delle quali è la costruzione di una griglia di elementi finiti (FE), la scelta di un sistema di coordinate globale rispetto all'intera struttura e un sistema locale associato all'elemento finito.

Il passaggio cruciale consiste nel definire le funzioni della forma, che forniscono la definizione di spostamenti all'interno dell'elemento finito a causa del movimento dei suoi nodi. Esistono diversi modi di costruire le funzioni di una forma, ma devono garantire l'adempimento di diverse condizioni per l'approssimazione delle funzioni degli spostamenti.

• Soddisfazione della continuità degli spostamenti non solo ai nodi degli elementi finiti, ma anche ai loro confini.
• Garantire la conservazione dei derivati ​​delle funzioni di spostamento, che sono legati al potenziale elastico.
• Il movimento dell'elemento finito come un numero intero rigido. Ciò significa che quando un elemento viene spostato come solido, i componenti del vettore di deformazione sono zero.

Problemi e soluzioni

La teoria dei metodi agli elementi finiti afferma che le relazioni FEM sono formate nel sistema di coordinate locale. Pertanto, i requisiti elencati per le funzioni del modulo vengono eseguiti automaticamente se gli assi del sistema locale sono orientati lungo i lati di un elemento finito. Tali casi hanno luogo per elementi finiti di strutture centrali, pannelli rettangolari e piastre rettangolari.

Ma in pratica esistono costruzioni con un contorno di definizione arbitraria. In questo caso, è necessario eseguire una trasformazione per approssimare gli spostamenti nel sistema di coordinate globali, che porta a discontinuità degli spostamenti ai limiti degli elementi finiti e, di conseguenza, alla perdita di precisione dei calcoli approssimativi.

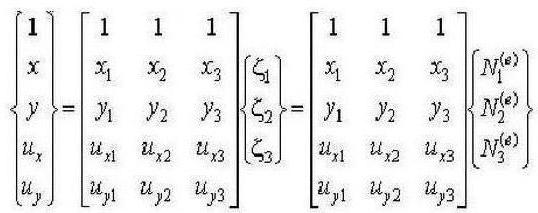
L'idea è nata dalla visualizzazione di un elemento piatto, quadrangolare finito di una forma generale su un quadrato con un sistema di coordinate locale, la cui origine è al centro di questa figura, e gli assi orientati sui suoi lati. Per l'ulteriore uso di elementi finiti sotto forma di un quadrato, è necessario stabilire una connessione uno-a-uno tra le coordinate locali di un quadrilatero arbitrario FE e il sistema di coordinate locale di FE nella forma di un quadrato. In effetti, per un elemento finito quadrato, le funzioni della forma sono costruite piuttosto semplicemente.

Metodo ad elementi finiti per calcoli di piastre

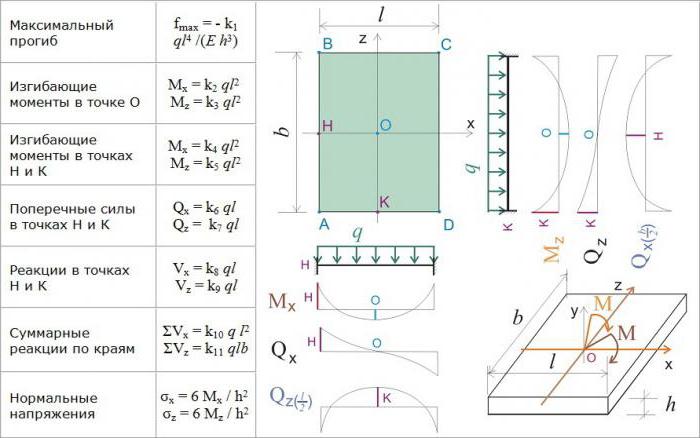
Un piatto è un inserto o un corpo cilindrico la cui altezza è molto più piccola della dimensione del piano. La dimensione dell'altezza si chiama spessore della lamiera. Il piano che divide l'altezza della piastra a metà è chiamato il piano mediano o di riferimento. La linea di intersezione della superficie laterale con il piano mediano è chiamata il contorno della piastra.

Si considera una piastra sottile, per la quale il rapporto tra lo spessore e le dimensioni minori del piano è compreso tra h≤L / 5, dove h è lo spessore della piastra, L è la sua larghezza.

Una piastra è considerata rigida se, sotto l'azione di un carico trasversale, la sua massima deflessione durante la deformazione non supera 1/5 del suo spessore.

Quando si calcola con il metodo FE, il sistema di coordinate viene prima inserito: X ₁ , X ₂ e X ₃ . L'inizio degli assi X ₁ e X ₂ si trova nel piano medio. L'asse X _{3 è} orientato lungo il piano normale rispetto al piano mediano.

I calcoli sono generalmente ridotti al calcolo dello spostamento (spostamento) di una piastra in un determinato punto sotto l'influenza di carichi (forze). In un punto arbitrario della piastra, che è considerato un corpo tridimensionale, compaiono tre direzioni di movimento: U ₁ , U ₂ , U ₃ . La definizione è il movimento lungo il piano normale rispetto al piano mediano, che è chiamato deflessione ed è indicato dalla lettera W.

Si considera che i calcoli vengano eseguiti se, da un dato carico (e questo di solito è distribuito uniformemente, diretto verso la superficie), viene stabilito un metodo per calcolare gli spostamenti U e lo spostamento W in un punto arbitrario della piastra. Le relazioni FEM si basano sulle disposizioni della teoria tecnica dell'elasticità proposta dal fisico Kirchhoff.

Le ipotesi di Kirchhoff

Il metodo degli elementi finiti si basa in gran parte su ipotesi formulate nel 1845 dal fisico tedesco G. Kirgofom. L'ipotesi normale diretta afferma che qualsiasi linea retta normale al piano mediano della placca non deformata rimane diritta e normale alla superficie media della placca deformata, e la lunghezza della retta non cambia. La sua essenza risiede nell'assenza di uno spostamento tra gli strati della piastra di spessore.

Se gli assi delle coordinate cartesiane sono posizionati in modo che i piani X ₁ , X ₂ coincidano con il piano mediano, allora le seguenti uguaglianze seguono dalla prima parte dell'ipotesi: y ₁₃ = 0, y ₂₃ = 0. L'ipotesi circa l'immutabilità della lunghezza di una retta presuppone che la deformazione lineare nella direzione dell'asse X ₃ sia zero: ε ₃₃ = 0.

L'ipotesi circa l'assenza di pressione tra gli strati della piastra parallela alla superficie media suggerisce che le sollecitazioni σ ₃₃ rispetto alle sollecitazioni σ ₁₁ e σ ₂₂ possono essere trascurate, cioè, σ ₃₃ = 0.

L'ipotesi della non deformabilità del piano medio suggerisce che nel piano medio del piatto non ci siano deformazioni di tensione, compressione e taglio. Cioè, il piano mediano è neutro. Quindi in esso lo spostamento U ₁ = U ₂ = 0.

conclusione

Il metodo degli elementi finiti, che è ampiamente utilizzato nella costruzione e nella meccanica, consente di calcolare gli spostamenti di vari elementi soggetti a determinati carichi. Il sistema, formulato nel 1936 da scienziati sovietici, cominciò ad essere largamente usato solo decenni dopo, poiché richiedeva una grande quantità di calcoli. Con l'introduzione dei computer, questa attività è semplificata.