Quattro formule con cui è possibile calcolare l'area di un rombo. Proprietà del diamante

Un rombo è una figura speciale in geometria. A causa delle sue proprietà speciali, non esiste una, ma diverse formule con l'aiuto di cui viene calcolata l'area di un rombo. Quali sono queste proprietà e quali sono le formule più comuni per trovare l'area di questa figura? Vediamo.

Quale? forma geometrica chiamato un diamante

Prima di scoprire qual è l'area di un rombo, vale la pena di sapere che tipo di figura è.

Dal momento della geometria euclidea, un rombo è chiamato quadrilatero simmetrico, tutti e quattro i lati dei quali sono uguali tra loro in lunghezza e paralleli in coppie.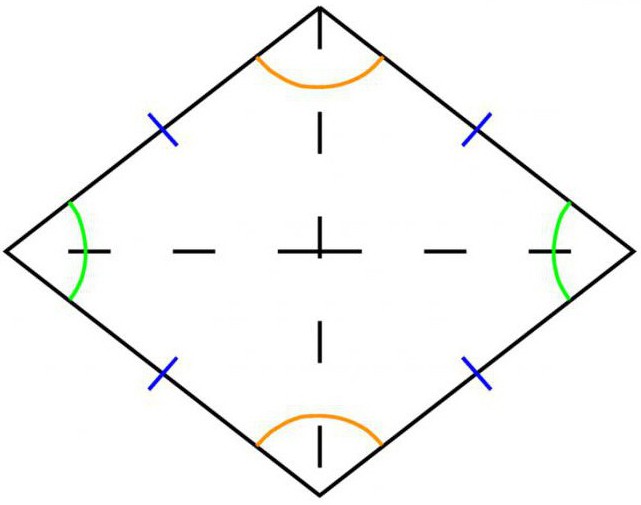

Origine del termine

Il nome di questa figura è venuto alla maggior parte delle lingue moderne dal greco, attraverso la mediazione del latino. Il "progenitore" della parola "rombo" è diventato il sostantivo greco ῥόμβος (tamburello). Sebbene gli abitanti del XX secolo, abituati a tamburi rotondi, è difficile immaginarli di una forma diversa, ma gli Elleni tradizionalmente hanno reso questi strumenti musicali non rotondi, ma a forma di diamante.

Nella maggior parte delle lingue moderne, questo termine matematico è usato, come in latino: rombus. Tuttavia, in inglese, i diamanti sono talvolta chiamati diamanti (diamanti o diamanti). A questa figura è stato dato un soprannome per la sua forma speciale, simile a una pietra preziosa. Di norma, tale termine non è usato per tutti i diamanti, ma solo per quelli il cui angolo di intersezione tra i suoi due lati è di sessanta o quarantacinque gradi.

Per la prima volta questa cifra fu menzionata negli scritti del matematico greco, che visse nel primo secolo di una nuova era: l'airone di Alessandria.

Quali proprietà ha questa figura geometrica?

Per trovare l'area di un rombo, devi prima sapere quali caratteristiche ha questa figura geometrica.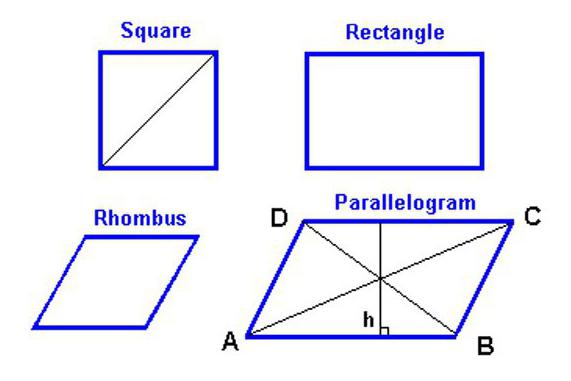

• Come già accennato nella definizione di un rombo, è un quadrilatero. E per il motivo che i suoi lati opposti sono paralleli l'uno all'altro in coppia, il rombo può anche essere chiamato parallelogramma, il che significa che la maggior parte delle proprietà di questa figura si applicano ad esso.
• Entrambi i rombi diagonali nel punto di intersezione sono equamente divisi in due. E a causa del fatto che si intersecano con un angolo di novanta gradi, le diagonali dividono la figura in 4 triangolo rettangolo.
• In ogni rombo, le diagonali dividono i suoi angoli in due, allo stesso tempo le loro bisettrici.
• Se ciascuna delle due diagonali di un rombo è elevata alla potenza di un quadrato, allora la loro somma sarà uguale al prodotto del quadrato del lato di questa figura e il numero quattro.
• Se si collegano le linee del centro dei quattro lati del rombo, la figura risultante sarà un rettangolo.
• Se un cerchio è inscritto in un diamante (indipendentemente dai suoi angoli), allora il suo punto centrale coinciderà con il centro di intersezione delle diagonali.
• Diamanti diagonali in contatto con gli assi della sua simmetria ad angoli di novanta gradi.
• Poiché tutti i lati di un rombo sono identici tra loro in lunghezza, il suo perimetro è calcolato dalla formula P = 4 x K (K è la lunghezza di uno dei lati).

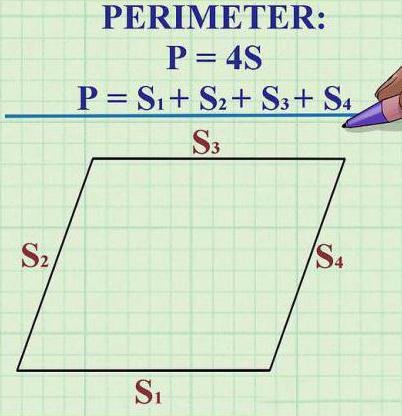
In quali condizioni un parallelogramma è un diamante

Come sai, ogni rombo è un parallelogramma, ma non tutti i parallelogrammi sono un rombo. Per affermare con precisione che una figura rappresentata è effettivamente un rombo, e non un semplice parallelogramma, deve corrispondere a una delle tre caratteristiche principali che distinguono un rombo. O tutti e tre contemporaneamente.

1. Il parallelogramma diagonale si interseca con un angolo di novanta gradi.
2. Le diagonali dividono gli angoli in due, fungendo da bisettrici.
3. Non solo paralleli, ma anche lati adiacenti hanno la stessa lunghezza. Questo, per inciso, è una delle principali differenze tra il rombo e il parallelogramma, poiché la seconda figura ha solo lati paralleli, ma non quelli adiacenti.

In quali condizioni è un quadrato rombo

Secondo le sue proprietà, in alcuni casi un rombo può diventare contemporaneamente un quadrato. Per confermare chiaramente questa affermazione, basta girare il quadrato in entrambe le direzioni di quarantacinque gradi. La figura risultante sarà un diamante, ciascuno degli angoli di cui è di novanta gradi.

Inoltre, per confermare che il quadrato è un rombo, puoi confrontare i segni di queste figure: in entrambi i casi, tutti i lati sono uguali, e le diagonali sono bisettrice e si intersecano con un angolo di novanta gradi.

Come trovare l'area di un rombo usando le sue diagonali

Nel mondo moderno su Internet è possibile trovare quasi tutti i materiali per eseguire i calcoli necessari. Quindi, c'è una massa di risorse dotate di programmi per il calcolo automatico dell'area di una particolare forma. Inoltre, se (come nel caso di un rombo) ci sono diverse formule per questo, allora c'è l'opportunità di scegliere quale di esse è più conveniente da usare. Tuttavia, prima di tutto, è necessario essere in grado di calcolare l'area di un rombo senza l'aiuto di un computer e orientarsi in formule. Per un diamante ce ne sono molti, ma i più famosi sono quattro.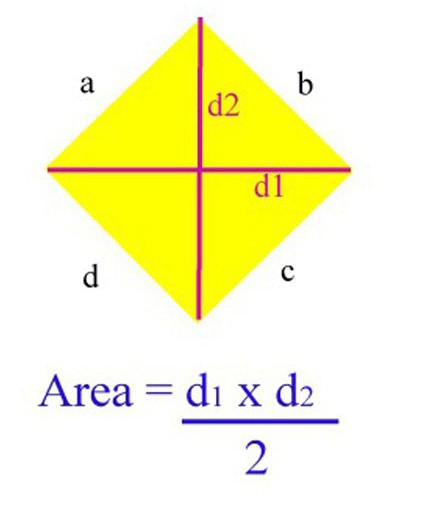

Uno dei modi più semplici e comuni per scoprire l'area di questa figura, se ci sono informazioni sulla lunghezza delle sue diagonali. Se il problema ha questi dati, in questo caso puoi applicare la seguente formula per trovare l'area: S = KM x LN / 2 (KM e LN sono la diagonale del rombo KLMN).

È possibile verificare la validità di questa formula in pratica. Supponiamo che un rombo KLMN abbia una diagonale KM della lunghezza di 10 cm e che il secondo LN sia di 8 cm, quindi sostituiamo questi dati nella formula sopra riportata e otteniamo il seguente risultato: S = 10 x 8/2 = 40 cm ² .

Formula per calcolare l'area di un parallelogramma

C'è un'altra formula. Come accennato sopra nella definizione di un rombo, non è solo un quadrilatero, ma anche un parallelogramma e ha tutte le caratteristiche di questa forma. In questo caso, per trovare la sua area, è ragionevole usare la formula usata per il parallelogramma: S = KL x Z. In questo caso, KL è la lunghezza del lato parallelogramma (rombo), e Z è la lunghezza dell'altezza disegnata su questo lato.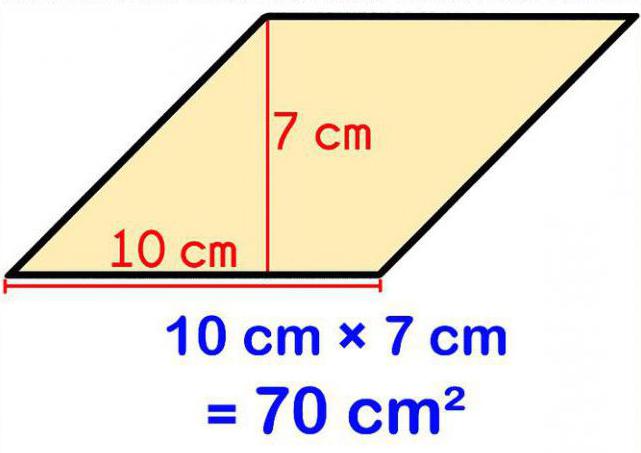

In alcuni compiti, la lunghezza del lato non è data, ma il perimetro del diamante è noto. Dal momento che la formula per trovarlo era indicata sopra, può essere usata per scoprire la lunghezza del lato. Quindi, il perimetro della figura è di 10 cm. La lunghezza del lato può essere riconosciuta invertendo la formula perimetrale e dividendo 10 per 4. Il risultato sarà 2,5 cm - questa è la lunghezza desiderata del lato rombo.

Ora vale la pena provare a sostituire questo numero nella formula, sapendo che anche la lunghezza al lato è di 2,5 cm. Ora proveremo a mettere questi valori nella formula dell'area del parallelogramma sopra menzionata. Risulta che l'area del rombo è S = 2,5 x 2,5 = 6,25 cm ² .

Altri modi per calcolare l'area del diamante

Coloro che hanno già padroneggiato i seni e i coseni possono usare le formule che li contengono per trovare l'area di un rombo. L'esempio classico è la seguente formula: S = KM ² x Sin KLM. In questo caso, l'area della figura è uguale al prodotto dei due lati del rombo moltiplicato per il seno dell'angolo tra di loro. E poiché nel rombo tutti i lati sono uguali, è più facile produrre immediatamente un lato in un quadrato, come mostrato nella formula.

Controlliamo questo schema in pratica, e non solo per un rombo, ma per un quadrato, che, come è noto, ha tutti gli angoli diritti, il che significa che sono di novanta gradi. Supponiamo che uno dei lati sia di 15 cm. È anche noto che il seno di un angolo di 90 ° è uno. Quindi, secondo la formula, S = 15 x 15 x Sin 90 ° = 255x1 = 255 cm ^2.

Oltre a quanto sopra, in alcuni casi viene utilizzata un'altra formula, utilizzando il seno per determinare l'area del rombo: S = 4 x R ² / Sin KLM. In questa variante, viene utilizzato il raggio del cerchio inscritto nel diamante. Sorge al potere di un quadrato e moltiplica per quattro. E l'intero risultato è diviso per il seno dell'angolo adiacente alla figura inscritta.

Ad esempio, per la semplicità dei calcoli riprenderemo il quadrato (il seno del suo angolo sarà sempre uguale a uno). Il raggio del cerchio inscritto in esso è di 4,4 cm, quindi l'area del rombo sarà calcolata come segue: S = 4 x 4.4 ² / Sin 90 ° = 77,44 cm ²

Le formule di cui sopra per trovare il raggio di un rombo sono lontane dalle uniche del loro genere, ma sono le più facili da capire e eseguire calcoli.