Come costruire un grafico di una funzione lineare. esempi
Per capire come tracciare una funzione lineare, è importante capire l'essenza stessa della funzione. Una funzione è un modello di dipendenza delle modifiche di un parametro su un altro.
L'argomento delle dipendenze funzionali è tradizionalmente aperto con dipendenza funzionale lineare. La lineare è la dipendenza più semplice. Il grafico della funzione lineare è dritto.
Vita e funzione
Nella vita, le dipendenze lineari si trovano solitamente nei processi artificiali ideali, i cui cambiamenti sono considerati permanenti. Ad esempio, quando una persona va da qualche parte a una velocità costante.
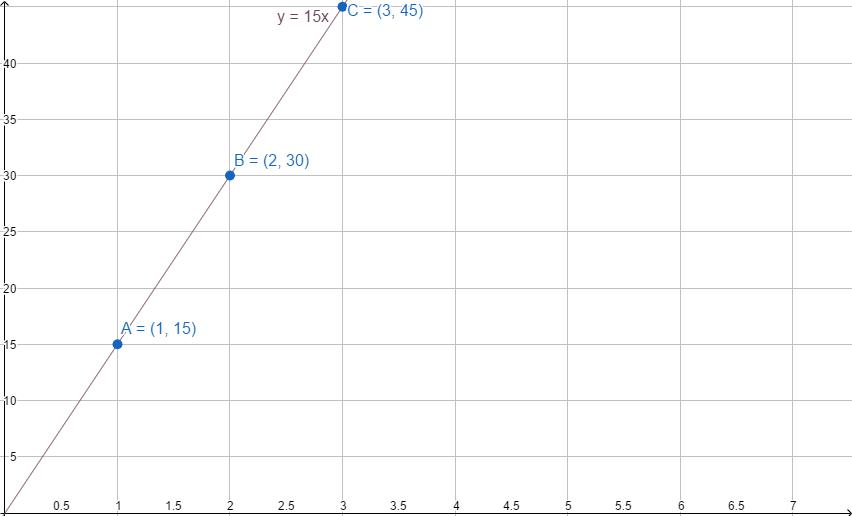
La distanza percorsa da una persona su una bicicletta varia in modo lineare a seconda del numero di ore di viaggio. Se guida 15 chilometri in un'ora (punto A), poi in due ore percorrerà 30 chilometri (punto B), in tre ore - 45 (punto C).
Ad
La dipendenza è descritta dall'equazione y = 15x. Come tracciare una funzione lineare in questo caso?
- trova le coordinate dei punti che sono la soluzione dell'equazione;
- costruiscile su un piano di coordinate;
- collega questi punti a una linea.
Descrizione dell'algoritmo
La ricerca delle coordinate dei punti che sono soluzioni dell'equazione si riduce alla ricerca di due punti che definiscono in modo univoco una linea. Sebbene sia sufficiente scegliere due diversi valori di x e trovare i valori corrispondenti di y, è possibile trovare tre coppie di valori per l'autocontrollo. Ciò ti consentirà di identificare rapidamente un possibile errore nei calcoli. Spesso il primo valore di x viene scelto come zero.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
Il secondo valore di x per k grande è meglio scegliere accanto al primo. Altrimenti, ci sarà una forte dispersione nei valori di y e x, ad esempio, a x = 4 nell'equazione considerata, y = 60. In ogni caso, prima di tracciare una funzione lineare sui punti trovati, viene selezionata una scala.
| y = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| y = 0 | y = 25 |
Coefficiente per x
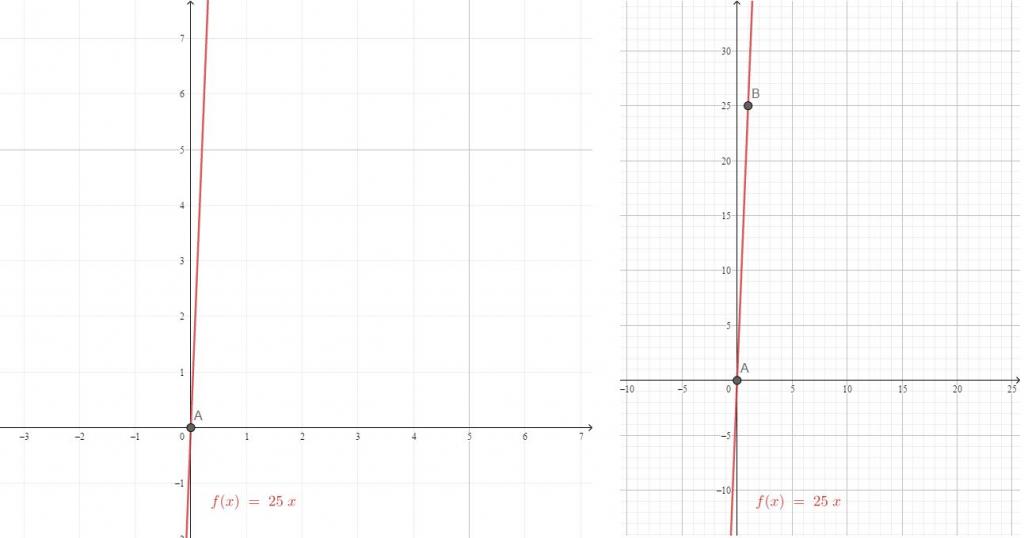
L'equazione di una funzione lineare è della forma y = kx + b. A seconda della variazione del coefficiente per lo sconosciuto, cambia anche la natura del grafico della funzione lineare y = kx.
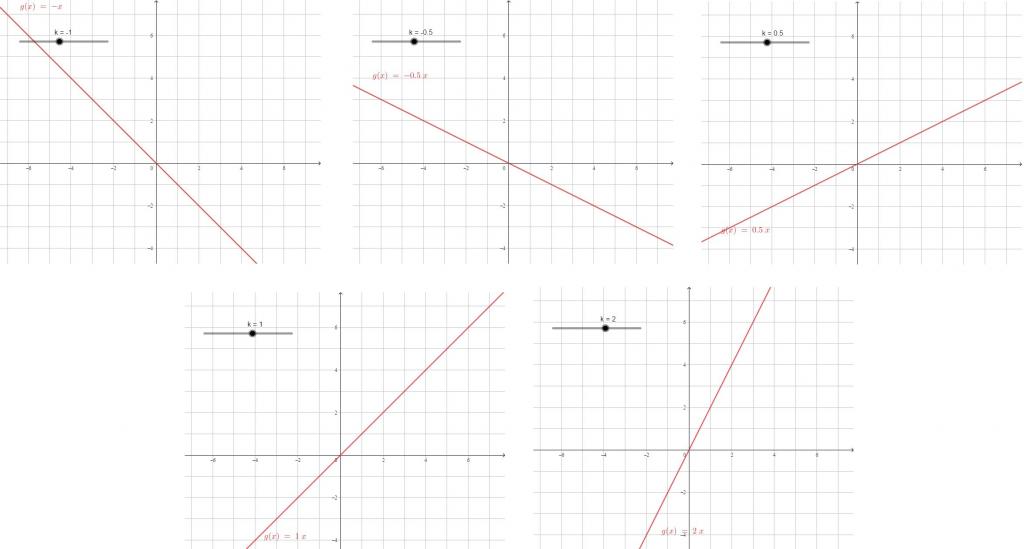
Maggiore è il coefficiente del modulo, maggiore è la pendenza della retta, più forte è lo stesso cambiamento in valori x i valori di y cambiano. Il coefficiente di x è il coefficiente di proporzionalità.
Rapporto gratuito
Il coefficiente libero è una costante che non dipende dai cambiamenti nel valore di x. Mostra dove la linea interseca OY.
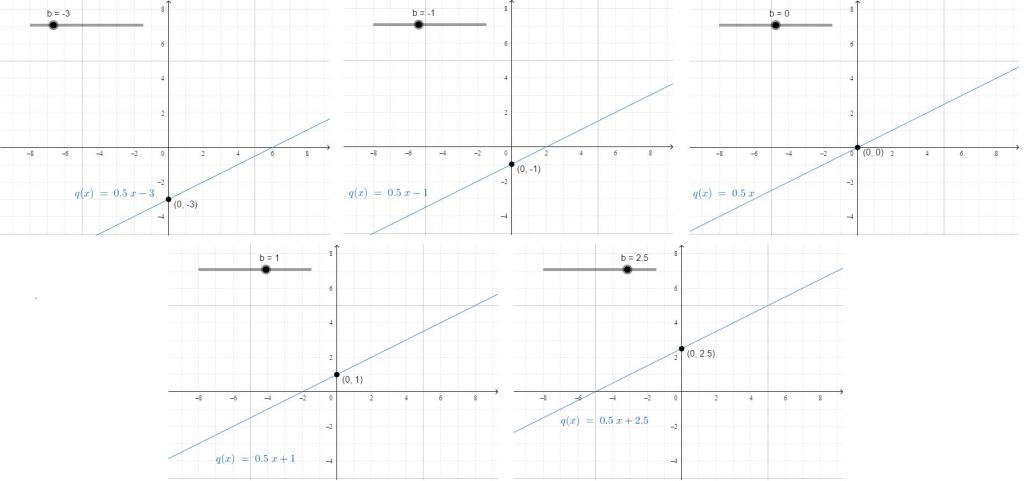
Ad esempio, una persona camminava a 10 chilometri dalla mattina fino alle 12 del pomeriggio, quindi ha guidato una bicicletta per tre ore. Poi la distanza percorsa per il giorno: y = 15 × 3 + 10. Se vuoi calcolare una formula per calcolare la distanza alla fine di ogni ora dai tre che ha guidato su una bicicletta, puoi usare: y = 15x + 10. All'una giorno ha guidato 15 × 1 e altri 10 passati, alle due ha guidato 15 × 2, ma ha superato tutti gli stessi 10.
Il grafico della funzione lineare y = kx + b descrive una linea che ha una pendenza k e interseca OY nel punto con coordinate (0, b). L'analisi dell'equazione consente spesso di risolvere i problemi senza creare un grafico. Ma per lavorare nella mente, le azioni devono essere ben collegate al materiale visivo.
Ad
Ad esempio, il compito è quello di trovare i punti di intersezione y = - x 2 ey = 0.5x + 5. La prima funzione è decrescente, la seconda è crescente, la prima è inferiore alla seconda, perché i rami della parabola sono in basso e il vertice è all'origine. Una funzione lineare dovrebbe avere un angolo di inclinazione molto più grande per essere più ripido e attraversare uno dei rami della parabola. Pertanto, è possibile determinare senza ambiguità che non ci sono punti di intersezione senza costruire un grafico e senza effettuare sostituzioni.
Casi speciali
- Quando non esiste un coefficiente libero, è (in effetti) uguale a zero, il che significa che la linea retta interseca OY a zero.
- Quando non ci sono x o y sconosciuti, ye x sono indipendenti l'uno dall'altro. Ad esempio, y = 5. Indipendentemente dal valore x, y sarà sempre 5. Graficamente, questo può essere rappresentato come una linea retta parallela a OX.
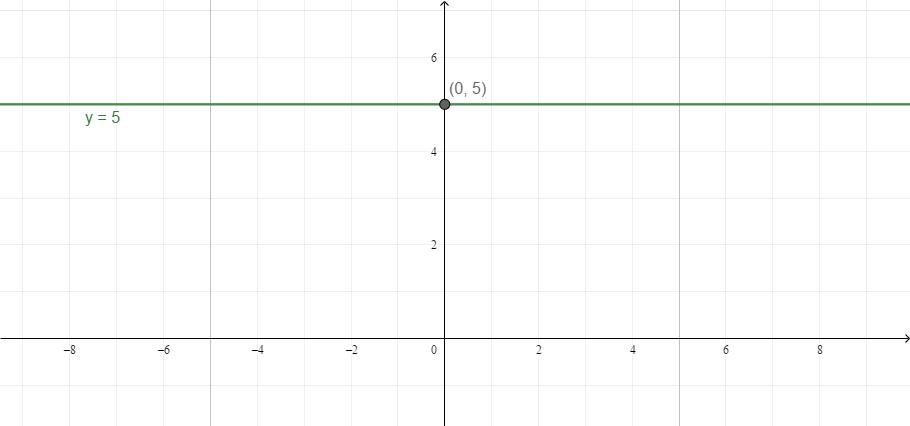
- Lo stesso vale per il caso in cui la variabile x è uguale al numero: la variabile x ha un valore costante.
Analizzando l'equazione prima ancora di tracciare una funzione lineare, è possibile scoprire la sua posizione approssimativa su OY e l'angolo di inclinazione, e quindi la pendenza. Questo aiuta non solo a trovare la giusta scala e costruire un grafico, ma anche a risolvere alcuni problemi nella mente.