Come calcolare l'area di un triangolo
Il triangolo è una figura ben nota. E questo, nonostante la ricca varietà delle sue forme. Rettangolare, equilatero, acuto, equilatero, ottuso. Ognuno è diverso. Ma per chiunque tu abbia bisogno di conoscere l'area del triangolo.
Comune per tutte le formule di triangoli che utilizzano la lunghezza dei lati o delle altezze
Le designazioni adottate in loro: le parti - a, b, c; altezze sui lati corrispondenti n e , n in , n con .
1. L'area di un triangolo è calcolata come il prodotto di ½, i lati e l'altezza calata su di esso. S = ½ * a * n a . Allo stesso modo, dovresti scrivere la formula per gli altri due lati.
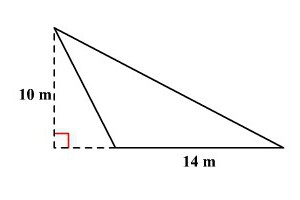
2. La formula dell'airone, in cui compare il semi-perimetro (è abitualmente contraddistinta dalla piccola lettera p, in contrasto con il perimetro completo). Il semi-perimetro deve essere contato come segue: mettere insieme tutti i lati e dividerli per 2. La formula semi-perimetro: p = (a + b + c) / 2. Quindi l'uguaglianza per l'area della figura è simile a questa: S = √ (p * (p - a) * ( p - c) * (p - c)).
Ad
3. Se non si desidera utilizzare un semi-perimetro, è utile una formula in cui sono presenti solo le lunghezze dei lati: S = ¼ * √ (((a + b + c) * (b + c - a) * (a + c - b) * (a + b - c)). È un po 'più lungo del precedente, ma sarà d'aiuto, se hai dimenticato come trovare un semi-perimetro.
Formule generali in cui appaiono gli angoli di un triangolo
Designazioni richieste per leggere le formule: α, β, γ - angoli. Si trovano di fronte ai lati a, b, c, rispettivamente.
1. Secondo esso, metà del prodotto di due lati e il seno dell'angolo tra di loro è uguale all'area del triangolo. Cioè: S = ½ a * b * sin γ. Allo stesso modo, le formule dovrebbero essere scritte per gli altri due casi.
2. L'area di un triangolo può essere calcolata da un lato e tre angoli noti. S = (a 2 * sin β * sin γ) / (2 sin α).
3. C'è anche una formula con un lato ben noto e due angoli adiacenti. Assomiglia a questo: S = c 2 / (2 (ctg α + ctg β)).
Le ultime due formule non sono le più facili. Ricordateli abbastanza difficili.
Formule generali per la situazione in cui sono noti i raggi di cerchi inscritti o circoscritti.
Ulteriori designazioni: r, R - radi. Il primo è usato per il raggio del cerchio inscritto. Il secondo è per il descritto.
Ad
1. La prima formula con cui viene calcolata l'area di un triangolo è collegata con un semi-perimetro. S = p * r. In un altro modo, può essere scritto come segue: S = ½ r * (a + b + c).
2. Nel secondo caso, dovrai moltiplicare tutti i lati del triangolo e dividerli per il raggio quadruplo del circumcircle. In termini letterali, assomiglia a questo: S = (a * c * s) / (4R).
3. La terza situazione ti consente di fare a meno di conoscere i lati, ma saranno richiesti i valori di tutti e tre gli angoli. S = 2 R2 2 sin α * sin β * sin γ.
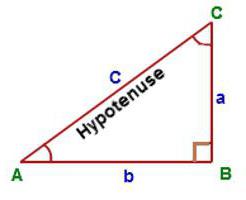
Caso speciale: triangolo rettangolo
Questa è la situazione più semplice, poiché richiede la conoscenza solo della lunghezza di entrambe le gambe. Sono indicati con lettere latine a e c. L'area di un triangolo rettangolo è uguale alla metà dell'area del rettangolo completata.
Ad
Matematicamente, assomiglia a questo: S = ½ a * c. È ricordato più facilmente. Poiché sembra una formula per l'area di un rettangolo, appare solo un'altra frazione, che significa metà.
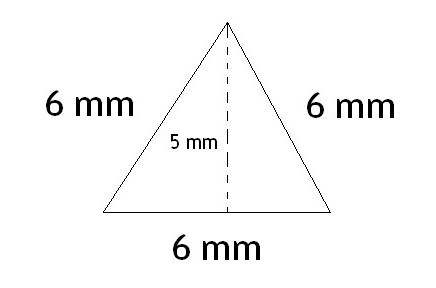
Caso speciale: triangolo isoscele
Poiché ha due lati uguali, alcune formule per la sua area sembrano un po 'semplificate. Ad esempio, la formula di Heron, che calcola l'area di un triangolo isoscele, assume la forma seguente:
S = ½ in √ (((+ a + ½ in) * (a - ½ in)).
Se lo converti, diventerà più breve. In questo caso, la formula di Heron per un triangolo isoscele è scritta come:
S = in √ (4 * a 2 - b 2 ).
Un po 'più semplice di un triangolo arbitrario, la formula dell'area appare se i lati e l'angolo tra di essi sono noti. S = ½ a 2 * sin β.
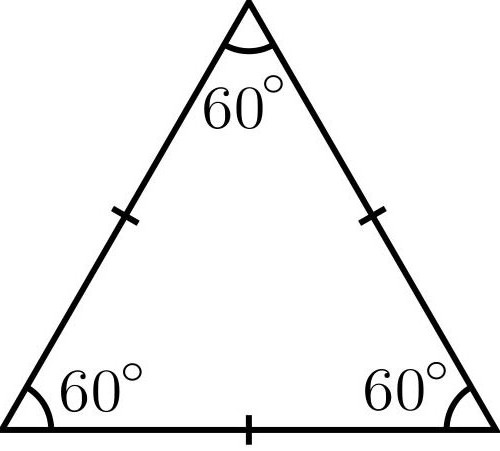
Caso speciale: triangolo equilatero
Di solito in problemi su di lui è noto il lato o si può in qualche modo scoprire. Quindi la formula, che è l'area di un triangolo, appare così:
S = (a 2 √3) / 4.
Cerca di trovare l'area, se il triangolo è raffigurato su carta a scacchi
La più semplice è la situazione in cui il triangolo destro è disegnato in modo che le sue gambe coincidano con le linee del foglio. Quindi devi solo contare il numero di celle che si adattano alle gambe. Quindi moltiplicale e dividi per due.
Quando il triangolo è ad angolo acuto o ottuso, deve essere disegnato sul rettangolo. Quindi nella forma risultante ci saranno 3 triangoli. Uno è quello dato nel problema. E gli altri due - ausiliari e rettangolari. Determina l'area delle ultime due necessità del metodo sopra. Quindi conta l'area del rettangolo e sottrai da esso quelli calcolati per l'ausiliario. L'area del triangolo è definita.
Ad
Molto più difficile è la situazione in cui nessuno dei due lati del triangolo coincide con le linee del foglio. Quindi deve essere inscritto in un rettangolo in modo che i vertici della figura originale si trovino ai suoi lati. In questo caso, ci saranno tre triangoli rettangolari ausiliari.
Un esempio del problema sulla formula di Gerona
Condizioni. Alcuni triangoli hanno lati. Sono uguali a 3, 5 e 6 cm. Devi conoscere la sua area.
La decisione Prima di tutto è necessario contare il semi-perimetro di un triangolo. Rendi la somma di tutti e tre, indicata nel problema, i numeri e dividila in due. I calcoli semplici portano al numero 7. Questo è il valore del mezzo metro.
Ora puoi calcolare l'area di un triangolo usando la formula sopra. sotto radice quadrata Risulta il prodotto di quattro numeri: 7, 4, 2 e 1. Cioè, l'area è √ (4 * 14) = 2 √ (14).
Se non è richiesta una maggiore precisione, è possibile estrarre la radice quadrata di 14. È pari a 3,74. Quindi l'area sarà pari a 7,48.
La risposta è S = 2 √14 cm 2 o 7,48 cm 2 .
Esempio di un problema con un triangolo rettangolo
Condizioni. Una gamba di un triangolo rettangolo è più lunga di 31 cm rispetto alla seconda: è necessario conoscere la loro lunghezza se l'area del triangolo è di 180 cm 2 .
La decisione Dovremo risolvere un sistema di due equazioni. Il primo è relativo al quadrato. Il secondo è con l'atteggiamento delle gambe, che è dato nel problema.
180 = ½ a * c;
Ad
a = a + 31.
Innanzitutto, il valore di "a" deve essere sostituito nella prima equazione. Risulta: 180 = ½ (in + 31) * c. Ha solo una quantità sconosciuta, quindi è facile da risolvere. Dopo aver aperto le parentesi, si ottiene un'equazione quadratica: in 2 + 31 in - 360 = 0. Dà due valori per "in": 9 e - 40. Il secondo numero non si adatta alla risposta, poiché la lunghezza del lato del triangolo non può essere un valore negativo.
Resta da calcolare la seconda tappa: aggiungi 31 al numero ottenuto. Ne risultano 40. Queste sono le quantità richieste nel problema.
La risposta è Le gambe del triangolo sono 9 e 40 cm.
Il compito di trovare il lato attraverso l'area, il lato e l'angolo del triangolo
Condizioni. L'area di un triangolo è di 60 cm 2 . È necessario calcolare uno dei suoi lati, se il secondo lato è di 15 cm e l'angolo tra di essi è 30º.
La decisione Sulla base della notazione accettata, il lato desiderato "a", noto "in", è un dato angolo "γ". Quindi la formula dell'area può essere riscritta come:
60 = ½ a * 15 * sin 30º. Qui il seno di 30 gradi è 0,5.
Dopo la trasformazione, "a" è uguale a 60 / (0,5 * 0,5 * 15). Questo è 16.
La risposta è Il lato richiesto è di 16 cm.
Il problema di un quadrato inscritto in un triangolo rettangolo
Condizioni. La parte superiore del quadrato con un lato di 24 cm coincide con l'angolo retto del triangolo. Altri due si trovano sulle gambe. Il terzo appartiene all'ipotenusa. La lunghezza di una gamba è di 42 cm. Qual è l'area di un triangolo rettangolo?
La decisione Considera due triangoli rettangoli. Il primo è indicato nell'attività. Il secondo è basato sulla nota gamba del triangolo originale. Sono simili, poiché hanno un angolo comune e sono formati da linee parallele.
Quindi i rapporti delle loro gambe sono uguali. Le gambe del triangolo più piccolo sono 24 cm (lato del quadrato) e 18 cm (la gamba di 42 cm viene sottratta dal lato del quadrato di 24 cm). Le gambe corrispondenti del grande triangolo sono 42 cm e x cm. È questa "x" che è necessaria per calcolare l'area del triangolo.
18/42 = 24 / x, cioè x = 24 * 42/18 = 56 (cm).
Quindi l'area è uguale al prodotto di 56 e 42, diviso in due, cioè 1176 cm 2 .
La risposta è L'area richiesta è 1176 cm 2 .