Come trovare l'area del poligono?

Nei problemi di geometria è spesso richiesto il calcolo dell'area di un poligono. Inoltre, può avere una forma piuttosto diversa - dal triangolo familiare a una certa n-gon con un numero inimmaginabile di vertici. Inoltre, questi poligoni sono convessi o concavi. In ogni situazione si suppone di costruire sull'aspetto della figura. Quindi risulta scegliere il modo migliore per risolvere il problema. La forma potrebbe essere corretta, il che semplifica in modo significativo la soluzione del problema.

Un po 'di teoria poligonale

Se vengono disegnate tre o più linee rette che si intersecano, allora formano una certa figura. Che è un poligono. Per il numero di punti di intersezione, diventa chiaro quanti vertici avrà. Danno il nome della figura risultante. Potrebbe essere:

• triangolo;
• quadrangolo;
• penta o esagono e così via.

Tale figura sarà certamente caratterizzata da due disposizioni:

1. I lati adiacenti non appartengono a una linea retta.
2. I punti non adiacenti non hanno punti in comune, cioè non si intersecano.

Per capire quali vertici sono adiacenti, devi vedere se appartengono allo stesso lato. Se è così, il prossimo. Altrimenti, possono essere collegati da un segmento, che deve essere chiamato diagonale. Possono essere disegnati solo in poligoni con più di tre vertici.

Quali sono i loro tipi?

Un poligono con più di quattro angoli può essere convesso o concavo. La differenza di quest'ultimo è che alcuni dei suoi vertici possono trovarsi sui lati opposti di una linea retta tracciata attraverso un lato arbitrario del poligono. In uno convesso, tutti i vertici si trovano sempre su un lato di tale linea.

Nel corso di geometria della scuola, la maggior parte del tempo viene data a figure esattamente convesse. Pertanto, nei problemi è richiesto di scoprire l'area di un poligono convesso. Poi c'è una formula attraverso il raggio del cerchio circoscritto, che ti permette di trovare il valore desiderato per qualsiasi forma. In altri casi, non esiste una soluzione unica. Per un triangolo, la formula è una, e per un quadrato o trapezio completamente diverso. In situazioni in cui la forma è irregolare o ci sono molti picchi, è consuetudine dividerli in semplici e familiari.

Cosa fare se un pezzo ha tre o quattro vertici?

Nel primo caso, sarà un triangolo e puoi utilizzare una delle formule:

• S = 1/2 * a * n, dove a è il lato, n è l'altezza ad esso;
• S = 1/2 * a * b * sin (A), dove aeb sono lati di un triangolo, A è l'angolo tra lati noti;
• S = √ (p * (p - a) * (p - c) * (p - c)), dove c è il lato del triangolo, al già marcato due, p è il semi-perimetro, cioè la somma di tutti e tre i lati, divisi in due .

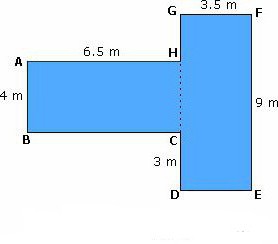
Una figura con quattro vertici può essere un parallelogramma:

• S = a * n;
• S = 1/2 * d ₁ * d ₂ * sin (α), dove d ₁ e d ₂ sono diagonali, α è l'angolo tra di loro;
• S = a * in * sin (α).

Formula per aree del trapezio: S = n * (a + b) / 2, dove a e b sono le lunghezze delle basi.

Cosa fare con un poligono regolare con più di quattro vertici?

Per cominciare, una tale figura è caratterizzata dal fatto che in essa tutti i lati sono uguali. Inoltre, il poligono ha gli stessi angoli.

Se un cerchio è descritto attorno a una tale figura, allora il suo raggio coinciderà con il segmento dal centro del poligono a uno dei vertici. Pertanto, per calcolare l'area di un poligono regolare con un numero arbitrario di vertici, abbiamo bisogno della seguente formula:

S _n = 1/2 * n * R _n ² * sin (360º / n), dove n è il numero di vertici del poligono.

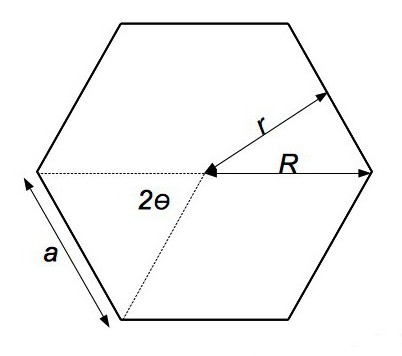
Da questo è facile ottenerne uno che sia utile per casi speciali:

1. triangoli: S = (3√3) / 4 * R ² ;
2. quadrato: S = 2 * R ² ;
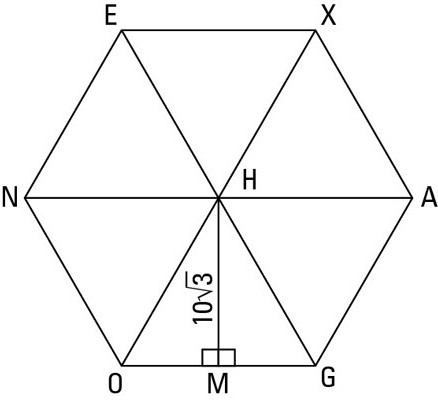
3. esagono: S = (3√3) / 2 * R ² .

La situazione con la figura sbagliata

La via d'uscita per scoprire l'area di un poligono, se non è corretta e non può essere attribuita a nessuna delle figure precedentemente note, è l'algoritmo:

• rompilo in forme semplici, come i triangoli, in modo che non si intersechino;
• calcola la loro area usando qualsiasi formula;
• sommare tutti i risultati.

Cosa fare se le coordinate dei vertici del poligono sono indicate nel problema?

Cioè, è noto un insieme di coppie di numeri per ogni punto che limitano i lati della figura. Solitamente sono scritti come (x ₁ ; y ₁ ) per il primo, (x ₂ ; y ₂ ) per il secondo, e l'ennesimo vertice ha questi valori (x _n ; y _n ). Quindi l'area del poligono è definita come la somma di n termini. Ognuno di essi assomiglia a questo: ((y _{i + 1} + y _i ) / 2) * (x _{i + 1} - x _i ). In questa espressione, io varia da uno a n.

Va notato che il segno del risultato dipenderà dall'elusione della forma. Quando si utilizza la formula specificata e si sposta in senso orario, la risposta sarà negativa.

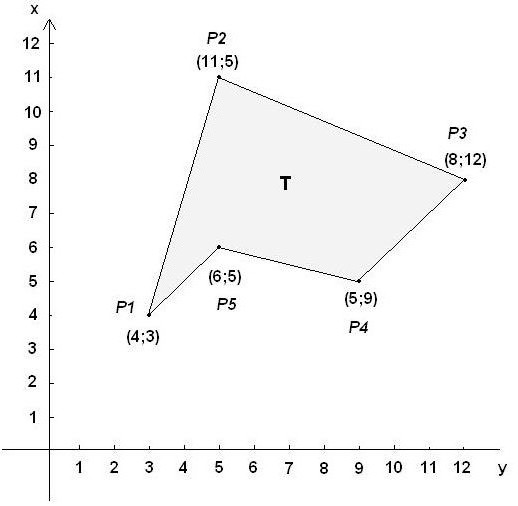
Compito di esempio

Condizioni. Le coordinate dei vertici sono date dai valori (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Richiesto per calcolare l'area del poligono.

La decisione Secondo la formula di cui sopra, il primo termine sarà (1,8 + 0,6) / 2 * (3,6 - 2,1). Qui devi solo prendere i valori per il gioco e X dal secondo e dal primo punto. Un semplice calcolo porterà al risultato 1.8.

Il secondo termine è ottenuto in modo simile: (2.2 + 1.8) / 2 * (2.3 - 3.6) = -2.6. Quando risolvi questi problemi non aver paura dei valori negativi. Tutto va come dovrebbe Questo è pianificato.

Allo stesso modo, si ottengono i valori per il terzo (0,29), il quarto (-6,365) e il quinto (2.96). Quindi l'area totale è: 1.8 + (-2.6) + 0.29 + (-6.365) + 2.96 = - 3.915.

Consiglio per risolvere il problema per cui il poligono è raffigurato su carta nella cella

Molto spesso, è sconcertante che solo la dimensione della cella sia presente nei dati. Ma risulta che non sono necessarie più informazioni. La raccomandazione per risolvere questo problema è dividere la forma in molti triangoli e rettangoli. La loro area è abbastanza semplice da contare la lunghezza delle parti, che sono quindi facili da piegare.

Ma spesso c'è un approccio più semplice. Consiste nel disegnare una figura in un rettangolo e calcolare il valore della sua area. Quindi conta le aree di quegli elementi che erano superflui. Sottrili dal totale. Questa opzione a volte comporta un numero leggermente inferiore di azioni.