Come trovare l'area di un triangolo isoscele?
La matematica è una scienza incredibile. Tuttavia, un tale pensiero arriva solo quando lo capisci. Per ottenere ciò, è necessario risolvere problemi ed esempi, disegnare diagrammi e disegni, dimostrare teoremi.
Il percorso per comprendere la geometria è attraverso la risoluzione dei problemi. Un esempio eccellente è il compito in cui è necessario trovare l'area di un triangolo isoscele.
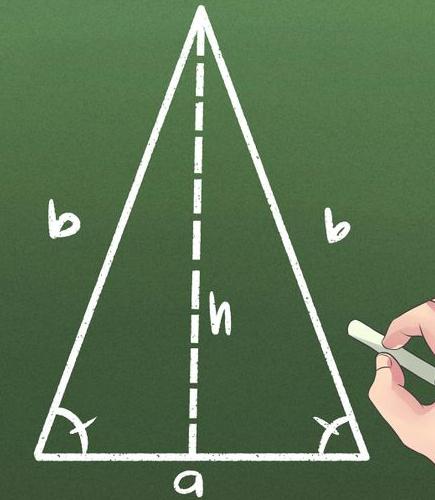
Cos'è un triangolo isoscele e in che cosa è diverso dagli altri?
Per non avere paura dei termini "altezza", "area", "base", "triangolo isoscele" e altri, è necessario partire da una base teorica.
Primo a proposito del triangolo. Questa è una figura piatta, formata da tre punti: i vertici, a loro volta, collegati da segmenti. Se due di loro sono uguali l'uno all'altro, allora il triangolo diventa isoscele. Questi lati furono chiamati il lato, e il resto divenne la base.
Ad
C'è un caso speciale di un triangolo isoscele: un equilatero, quando il terzo lato è uguale a due laterali.
Proprietà della forma
Dimostrano di essere fedeli assistenti nella risoluzione dei problemi che richiedono la ricerca dell'area di un triangolo isoscele. Pertanto, per conoscerli e ricordarli è necessario.
- Il primo di essi: gli angoli di un triangolo isoscele, un lato del quale è la base, sono sempre uguali tra loro.
- Anche la proprietà di ulteriori costruzioni è importante. Le altezze al lato spaiato, la mediana e il bisettrice coincidono.
- Questi segmenti, disegnati dagli angoli alla base del triangolo, sono uguali a coppie. Questo troppo spesso rende più facile trovare una soluzione.
- Due angoli uguali in esso contano sempre meno di 90 °.
- E infine: i cerchi inscritti e circoscritti sono costruiti in modo che i loro centri si trovino all'altezza della base del triangolo, che significa la mediana e la bisettrice.

Come riconoscere un triangolo isoscele in un problema?
Se, nel risolvere un compito, sorge la domanda su come trovare l'area di un triangolo isoscele, quindi devi prima capire che appartiene a questo gruppo. E questo aiuterà certi segni.
Ad
- Uguale a due angoli o due lati di un triangolo.
- Anche la bisettrice è una mediana.
- L'altezza del triangolo è la mediana o bisettrice.
- Uguale a due altezze, mediane o bisettrici di una figura.
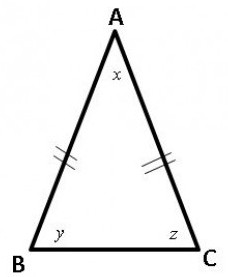
Designazione delle quantità adottate nelle formule considerate
Per semplificare come trovare l'area di un triangolo isoscele usando le formule, viene introdotta la sostituzione dei suoi elementi con lettere.
| La lettera nella formula | nome |
| e | fianco |
| in | lunghezza di base |
| n | altezza alla base |
| la | angolo di base |
| il | l'angolo tra i lati |
| designazione comune | zona |
Attenzione! È importante non confondere "a" con "A" e "b" con "B". Queste sono diverse quantità.
Formule che possono essere utilizzate in diversi compiti
Le lunghezze dei lati sono note e è necessario trovare l'area di un triangolo isoscele.
In questo caso, devi quadrare entrambi i valori. Il numero derivante dalla modifica del lato, moltiplicato per 4 e sottrarre il secondo da esso. Estratto dalla differenza risultante radice quadrata. La lunghezza della base divisa per 4. Due numeri si moltiplicano. Se scrivi queste azioni in lettere, ottieni la seguente formula:
Ad
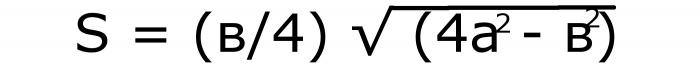
Lascia che sia registrato sotto №1.
Trova dai valori dei lati l'area di un triangolo isoscele. Una formula che può sembrare più semplice a qualcuno rispetto alla prima.
Il primo passo è trovare metà della base. Quindi trova la somma e la differenza di questo numero con il lato. Moltiplicare gli ultimi due valori ed estrarre la radice quadrata. L'ultimo passo è moltiplicare tutto della metà della base. L'uguaglianza delle lettere sarà simile a questa:
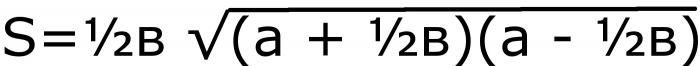
Questa è la formula numero 2.
Un modo per trovare l'area di un triangolo isoscele, se la base e l'altezza sono note.
Una delle formule più brevi. È necessario moltiplicare entrambi i valori dei dati e dividerli per 2. Ecco come sarà scritto:

Il numero di questa formula è 3.
Nell'attività sono noti i lati del triangolo e l'angolo tra la base e il lato.
Qui, per scoprire quale sarà l'area di un triangolo isoscele, la formula sarà composta da diversi fattori. Il primo di questi è il valore del seno dell'angolo. Il secondo è uguale al prodotto del lato alla base. Il terzo è una frazione di ½. Notazione matematica generale:

Il numero ordinale della formula è 4.
Nel problema sono indicati: il lato di un triangolo isoscele e l'angolo che si trova tra i suoi lati.
Come nel caso precedente, l'area si trova su tre fattori. Il primo è uguale al seno dell'angolo specificato nella condizione. Il secondo è il quadrato del lato. E quest'ultimo è anche pari alla metà dell'unità. Di conseguenza, la formula è scritta come:
Ad
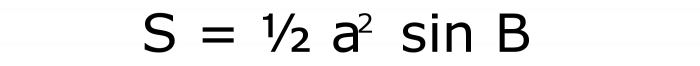
Il suo numero è 5.
La formula che ti permette di trovare l'area di un triangolo isoscele, se conosci la sua base e l'angolo che si trova di fronte.
Per prima cosa devi calcolare la tangente di mezzo angolo noto. Moltiplicare il numero risultante per 4. Piazza la lunghezza del lato, che viene quindi diviso per il valore precedente. Quindi, otteniamo la seguente formula:

Il numero dell'ultima formula è 6.
Esempi di compiti
Primo compito: è noto che la base di un triangolo isoscele è di 10 cm e la sua altezza è di 5 cm. È necessario determinare la sua area.
Per risolverlo, è logico scegliere la formula numero 3. Tutto è noto al suo interno. Sostituire numeri e contare. Si scopre che l'area è 10 * 5 / 2. Cioè, 25 cm 2 .

Il secondo compito: in un triangolo isoscele, vengono dati il lato e la base, che sono rispettivamente 5 e 8 cm. Trova la sua area.
Il primo modo Secondo la formula numero 1. Quando si squadrano la base, si ottiene il numero 64 e il quadruplo quadrato del lato è 100. Dopo aver sottratto dal secondo, il primo ne risulterà 36. La radice viene perfettamente estratta da essa, che è 6. La base divisa per 4 è 2. Il valore finale è definito come il prodotto 2 e 6, che è 12. Questa è la risposta: l'area richiesta è 12 cm 2 .
Il secondo modo. Secondo la formula numero 2. La metà della base è uguale a 4. La somma del lato e del numero trovato dà 9, la loro differenza è 1. Dopo aver moltiplicato, otteniamo 9. La rimozione della radice quadrata dà 3. E l'ultima azione, moltiplicando 3 per 4, che dà lo stesso 12 cm 2 .

Consiglio: come amare la matematica
Risolvendo problemi di geometria e determinando come trovare l'area di un triangolo isoscele, è possibile ottenere un'esperienza preziosa. Le opzioni più diverse per le attività eseguite, più facile è trovare la risposta in una nuova situazione. Pertanto, la regolare e indipendente esecuzione di tutti i compiti è la via per il successo dell'apprendimento del materiale.