Come realizzare un'equazione in linea retta su due punti: casi bidimensionali e tridimensionali
Una linea retta in geometria è uno degli elementi più importanti, dal momento che molte figure sono raccolte da esso, sia sull'aereo che nello spazio. Basta nominare un triangolo, un parallelogramma, un prisma, una piramide: tutti sono formati da linee rette che si intersecano. Questo articolo risponde alla domanda su come realizzare un'equazione in linea retta usando due punti.
Equazione della linea per casi bidimensionali e tridimensionali
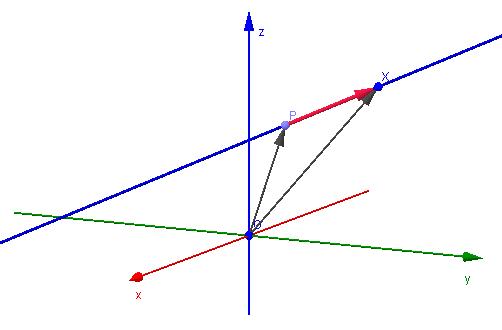
Prima di passare alla discussione sulla questione di come comporre un'equazione retta da due punti, si dovrebbe capire cosa è in gioco.
L'equazione di una retta è intesa come l'uguaglianza associata al sistema di coordinate adottato, e tutti i valori delle variabili che lo soddisfano devono trovarsi su una linea retta. Nei casi bidimensionali e tridimensionali, questa equazione può essere definita come segue:
Ad
Q = P + α * u¯
Qui Q è le coordinate di un punto arbitrario della linea, P è le coordinate di un punto specifico appartenente alla linea, u ¯ è il vettore di direzione, α è qualsiasi numero reale. Il vettore di direzione u è parallelo alla retta. Questa espressione è chiamata equazione parametrico-vettoriale.
Nel caso bidimensionale, ciascun punto sul piano è definito in modo univoco da due coordinate xey, quindi è possibile scrivere l'equazione della linea nella forma:
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Dove (x 0 ; y 0 ) sono le coordinate del punto noto della linea, (a; b) sono le coordinate del vettore di direzione. In una forma parametrica, questa equazione può essere riscritta come un sistema di due equazioni:
x = x 0 + α * a;
y = y 0 + α * b.
Esprimendo il parametro alfa ed equiparando le uguaglianze ottenute, arriviamo alla forma:
y = b / a * x + (y 0 -x 0 * b / a) o
y = A * x + C, dove A = b / a, C = (y 0 - x 0 * b / a)
L'espressione risultante è familiare a tutti gli studenti. Si chiama l'equazione generale di una linea su un piano.
Nello spazio, ogni punto è dato non da due, ma da tre coordinate, quindi la sua equazione parametrico-vettoriale assume la forma:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
L'equazione parametrico-vettoriale è conveniente da usare quando è necessario creare un'equazione di una retta passante per due punti.
Linea retta e due punti
Ora considera direttamente il problema dell'articolo. Come fare un'equazione diretta usando due punti? Per prima cosa, otteniamo un'equazione sul piano e poi la generalizziamo per il caso tridimensionale.
Supponiamo che ci siano due punti sul piano P (x 1 ; y 1 ) e Q (x 2 ; y 2 ). Se prendiamo la differenza tra le coordinate dei punti, otteniamo un vettore che è diretto da uno di essi all'altro. Questo vettore è uguale a:
PQ¯ (x 2 -x 1 ; y 2 -y 1 )
In questo caso, PQ¯ è diretto da P (l'inizio del segmento diretto) a Q (la sua fine). Poiché entrambi i punti appartengono alla linea, il vettore PQ¯ appartiene ad esso. Ciò significa che può essere considerato guida. L'equazione di una linea retta assume la forma:
Ad
(x; y) = (x 1 ; y 1 ) + α * (x 2 -x 1 ; y 2 -y 1 )
Qui abbiamo preso il punto P. Se lo sostituiamo con il punto Q, l'equazione non cambierà.
Come creare un'equazione di una linea retta nello spazio usando due punti? Riassumendo la formula risultante per l'aereo, otteniamo:
(x; y; z) = (x 1 ; y 1 ; z 1 ) + β * (x 2 -x 1 ; y 2 -y 1 ; z 2 -z 1 )
L'altra lettera per il parametro è presa per mostrare l'indipendenza di questa e delle equazioni precedenti.
Un esempio di risoluzione del problema
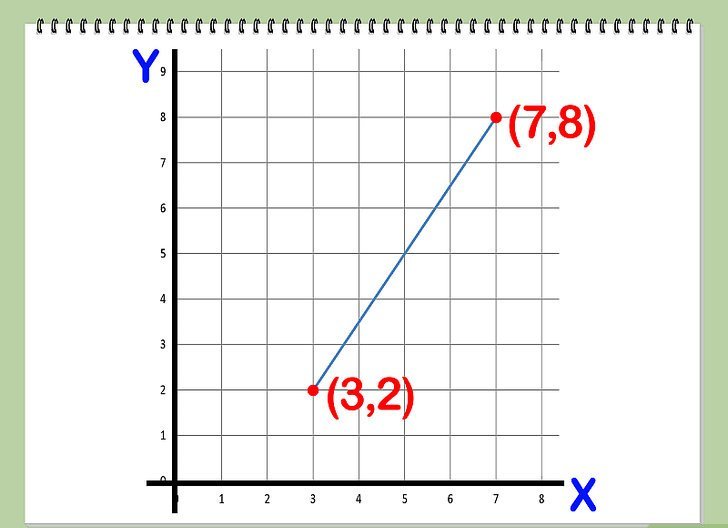
Avendo capito come fare un'equazione diretta per due punti, diamo un esempio dell'uso delle conoscenze acquisite per il caso bidimensionale.
Supponiamo che ci siano punti sul piano (3; -4) e (0; 7). È necessario fare un'equazione diretta attraverso due punti.
Calcola le coordinate del vettore guida:
(0-3; 7 - (- 4)) = (-3; 11)
L'equazione parametrico-vettoriale ha la forma:
(x; y) = (3; -4) + α * (- 3; 11)
Aprilo e portalo nella forma generale:
x = 3 - 3 * α => α = (x-3) / (- 3);
y = -4 + 11 * α => α = (y + 4) / 11;
(x-3) / (- 3) = (y + 4) / 11 =>
y = -11 / 3 * x + 7.
Abbiamo ottenuto l'equazione nella solita forma (generale). È possibile verificare la sua validità sostituendo le coordinate di entrambi i punti dalla condizione del problema.