Energia cinetica - l'energia del movimento dei corpi
L'energia potenziale e cinetica ci consente di caratterizzare lo stato di qualsiasi corpo. Se il primo è usato in sistemi di oggetti interagenti, quest'ultimo è associato al loro movimento. Questi tipi di energia, di norma, vengono considerati quando la forza che collega i corpi è indipendente dalla traiettoria del movimento. In questo caso, solo le posizioni iniziali e finali sono importanti.
Informazioni generali e concetti
L'energia cinetica del sistema è una delle sue caratteristiche più importanti. I fisici distinguono due tipi di tale energia a seconda del tipo di movimento:
• progressivo;
• rotazione.
L'energia cinetica (E k ) è la differenza tra l'energia totale del sistema e l'energia di riposo. Sulla base di questo, possiamo dire che è dovuto al movimento del sistema. Il corpo ha solo quando si muove. A riposo, l'oggetto è zero. L'energia cinetica di qualsiasi corpo dipende unicamente dalla velocità del movimento e dalle loro masse. L'energia totale del sistema dipende direttamente dalla velocità dei suoi oggetti e dalla loro distanza.
Formule di base
Nel caso in cui qualsiasi forza (F) agisca su un corpo che è a riposo in modo tale da entrare in movimento, possiamo parlare di fare il lavoro dA. Il valore di questa energia sarà più alto, più lavoro sarà svolto. In questo caso, la seguente uguaglianza è vera: dA = dE.
Dato il percorso percorso dal corpo (dR) e la sua velocità (dU), è possibile utilizzare la legge di 2 Newton, in base alla quale: F = (dU / dE) * m.
La legge di cui sopra viene utilizzata solo quando esiste un sistema di riferimento inerziale. C'è un'altra sfumatura importante che viene presa in considerazione nei calcoli. Il valore dell'energia è influenzato dalla scelta del sistema. Quindi, secondo il sistema SI, viene misurato in joule (J). L'energia cinetica del corpo è caratterizzata da una massa m, così come la velocità del movimento υ. In questo caso, sarà: E k = ((υ * υ) * m) / 2.
Basato sulla formula sopra, possiamo concludere che l'energia cinetica è determinata dalla massa e dalla velocità. In altre parole, è una funzione del movimento del corpo.
Energia nel sistema meccanico
L'energia cinetica è energia meccanica sistema. Dipende dalla velocità dei suoi punti. Data energia qualsiasi punto materiale è rappresentato dalla seguente formula: E = 1 / 2mυ 2, dove m è la massa di un punto, e υ è la sua velocità.
L'energia cinetica di un sistema meccanico è la somma aritmetica delle stesse energie di tutti i suoi punti. Può anche essere espresso dalla seguente formula: E k = 1 / 2Mυ c2 + Ec, dove υc è la velocità del centro di massa, M è la massa del sistema, Ec è l'energia cinetica del sistema quando si muove attorno al centro di massa.
Energia solida
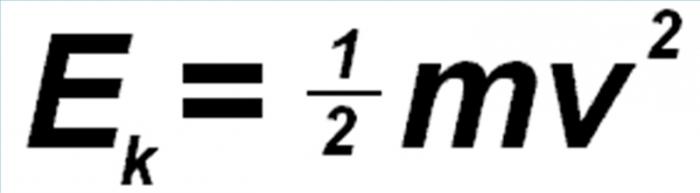L'energia cinetica del corpo, che si muove progressivamente, è determinata dalla stessa energia di un punto con una massa pari alla massa di tutto il corpo. Per il calcolo degli indicatori durante lo spostamento si applicano formule più complesse. Il cambiamento di questa energia del sistema nel momento del suo movimento da una posizione all'altra avviene sotto l'influenza di forze interne ed esterne applicate. È uguale alla somma del lavoro di Aue e A'u di queste forze durante questo movimento: E2 - E1 = Σu Aue + Σu A'u.
Questa uguaglianza riflette il teorema riguardante il cambiamento nell'energia cinetica. Con il suo aiuto vengono risolti i più diversi problemi di meccanica. Senza questa formula è impossibile risolvere una serie di compiti importanti.
Energia cinetica ad alta velocità
Se la velocità del corpo è vicina alla velocità della luce, l'energia cinetica del punto materiale può essere calcolata con la seguente formula:
E = m0c2 / √1-υ2 / c2 - m0c2,
dove c è la velocità della luce nel vuoto, m0 è la massa di un punto, m0c2 è l'energia di un punto. A bassa velocità (υ Durante la rotazione del corpo attorno all'asse, ciascuno dei suoi elementari volumi di massa (mi) descrive un cerchio di raggio ri. A questo punto, il volume ha una velocità lineare υi. Poiché viene considerato un solido, velocità angolare la rotazione di tutti i volumi sarà la stessa: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). L'energia cinetica di rotazione di un solido è la somma di tutte le stesse energie dei suoi volumi elementari: E = m1υ1 2/2 + miυi 2/2 + ... + mnυn 2/2 (2). Usando expression (1), otteniamo la formula: E = Jz ω 2/2, dove Jz è il momento di inerzia del corpo attorno all'asse Z. Quando si confrontano tutte le formule, diventa chiaro che il momento di inerzia è la misura dell'inerzia del corpo durante movimento rotatorio. La formula (2) è adatta per oggetti che ruotano attorno ad un asse fisso. L'energia cinetica di un corpo che si muove lungo il piano consiste nell'energia di rotazione e movimento traslatorio: E = mυc2 / 2 + Jz ω 2/2, dove m è la massa del corpo in movimento, Jz è il momento di inerzia del corpo attorno all'asse, υc è la velocità del centro di massa, ω è la velocità angolare. Il cambiamento nel valore dell'energia cinetica è strettamente correlato al potenziale. L'essenza di questo fenomeno può essere compresa attraverso la legge di conservazione dell'energia nel sistema. La somma di E + dP durante il movimento del corpo sarà sempre la stessa. Un cambiamento nel valore di E avviene sempre simultaneamente con una modifica di dP. Così, essi vengono trasformati, come se fluivano l'uno nell'altro. Un tale fenomeno può essere trovato in quasi tutti i sistemi meccanici. Per il calcolo del valore energetico viene scelto un momento arbitrario (è considerato quello iniziale) e un sistema di riferimento. È possibile determinare l'esatta quantità di energia potenziale solo nella zona di influenza delle forze che non dipendono dalla traiettoria del corpo quando si lavora. In fisica, queste forze sono chiamate conservative. Hanno una connessione costante con la legge di conservazione dell'energia. Se l'influenza esterna è minima o ridotta a zero, il sistema in esame sarà sempre in uno stato in cui anche la sua energia potenziale tenderà a zero. Ad esempio, una palla sollevata raggiungerà il limite di questa energia nel punto più alto della traiettoria di movimento e nello stesso momento inizierà a cadere. In questo momento, l'energia accumulata in volo viene convertita in movimento (lavoro eseguito). Per l'energia potenziale, in ogni caso, c'è un'interazione di almeno due corpi (nell'esempio con una palla, la gravità del pianeta lo influenza). L'energia cinetica può essere calcolata individualmente per qualsiasi corpo in movimento. L'energia potenziale e cinetica cambia esclusivamente nell'interazione dei corpi, quando la forza che agisce sul corpo svolge un lavoro, il cui valore è diverso da zero. In un sistema chiuso, il lavoro della forza di forza o dell'elasticità è uguale al cambiamento nell'energia potenziale degli oggetti con il segno "-": A = - (Ep2 - Ep1). Il lavoro della forza o dell'elasticità è uguale al cambiamento di energia: A = Ek2 - Ek1. Dal confronto di entrambe le equazioni è chiaro che il cambiamento nell'energia degli oggetti in un sistema chiuso equivale al cambiamento di energia potenziale ed è opposto nel segno: Ek2 - Ek1 = - (Ep2 - Ep1), o altrimenti: Ek1 + Ep1 = Ek2 + Ep2. Da questa uguaglianza è chiaro che la somma di queste due energie di corpi in un sistema meccanico chiuso e le forze interagenti di elasticità e aggressività rimangono sempre costanti. Sulla base di quanto precede, si può concludere che nel processo di studio di un sistema meccanico, l'interazione di energie potenziali e cinetiche dovrebbe essere considerata. 
Energia di rotazione del sistema
Movimento del corpo planare
Il cambiamento di energia nel sistema meccanico
Interconnessione energetica
Le potenzialità e le energie cinetiche sono strettamente correlate. La loro somma può essere rappresentata come l'energia totale del sistema. A livello molecolare, lo è energia interna corpo. È presente costantemente, purché vi sia almeno una certa interazione tra i corpi e il movimento termico. La scelta del sistema di riferimento
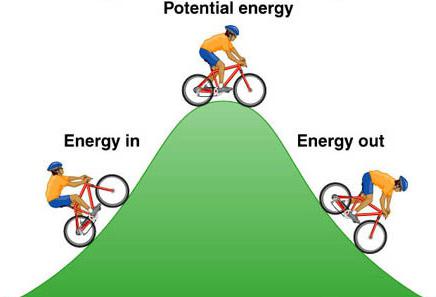
L'essenza della differenza tra potenziale ed energia cinetica
Interconnessione di diverse energie