Logaritmi: regole, proprietà di base e formule

Logaritmi e regole di azione con loro sono abbastanza capienti e semplici. Pertanto, per comprendere questo argomento non sarà difficile. Dopo aver appreso tutte le regole dei logaritmi naturali, qualsiasi problema verrà risolto autonomamente. La prima conoscenza di questo argomento può sembrare noiosa e insensata, ma fu con l'aiuto dei logaritmi che furono risolti molti problemi dei matematici del XVI secolo. "Di cosa si tratta?" - hai pensato. Leggi l'articolo fino alla fine e scopri che questa sezione della "Zarina delle scienze" potrebbe interessare non solo i matematici, gli scienziati delle scienze esatte, ma anche gli studenti della scuola secondaria ordinaria.

Definizione del logaritmo

Iniziamo con la definizione del logaritmo. Come molti libri di testo dicono: il logaritmo del numero b sulla base di un (log _a b) è un certo numero c per cui questa uguaglianza vale: b = a ^c . Cioè, in termini semplici, il logaritmo è un certo grado con cui costruiamo una base per ottenere un dato numero. Ma è importante ricordare che il logaritmo del modulo log _a b ha senso solo quando: a> 0; a è un numero diverso da 1; b> 0, quindi, concludiamo che il logaritmo può essere trovato solo per numeri positivi.

Classificazione dei logaritmi per base

I logaritmi possono essere qualsiasi numero positivo alla base. Ma ci sono anche due tipi: logaritmi naturali e decimali.

• Il logaritmo naturale - il logaritmo con base e (e è il numero di Eulero, numericamente approssimativamente uguale a 2.7, il numero irrazionale introdotto per la funzione esponenziale y = e ^x ) è denotato come ln a = log _e a;
• Il logaritmo decimale è il logaritmo con base 10, ovvero log ₁₀ a = lg a.

Regole di base dei logaritmi

Per prima cosa è necessario conoscere l'identità logaritmica di base: un ^{log _a b} = b, quindi seguire queste due regole di base:

• log _a 1 = 0 - poiché qualsiasi numero nel grado zero è 1;
• log _a a = 1.

Grazie alla scoperta del logaritmo, non è difficile per noi risolvere assolutamente qualsiasi equazione esponenziale, la cui risposta non può essere espressa in numeri naturali, ma solo irrazionale. Ad esempio: 5 ^x = 9, x = log ₅ 9 (poiché non esiste una x naturale per questa equazione).

Azioni con logaritmi

• log _a (x · y) = log _a x + log _a y - per trovare il logaritmo del prodotto, è necessario aggiungere i logaritmi dei fattori. Si noti che le basi dei logaritmi sono le stesse. Se scriviamo questo in ordine inverso, otteniamo la regola dell'aggiunta dei logaritmi.
• log _a xy = log _a x - log _a y - per trovare il logaritmo del particolare, è necessario trovare la differenza tra i logaritmi del dividendo e il divisore. Nota: i logaritmi hanno la stessa base. Quando scriviamo in ordine inverso, otteniamo la regola della sottrazione dei logaritmi.

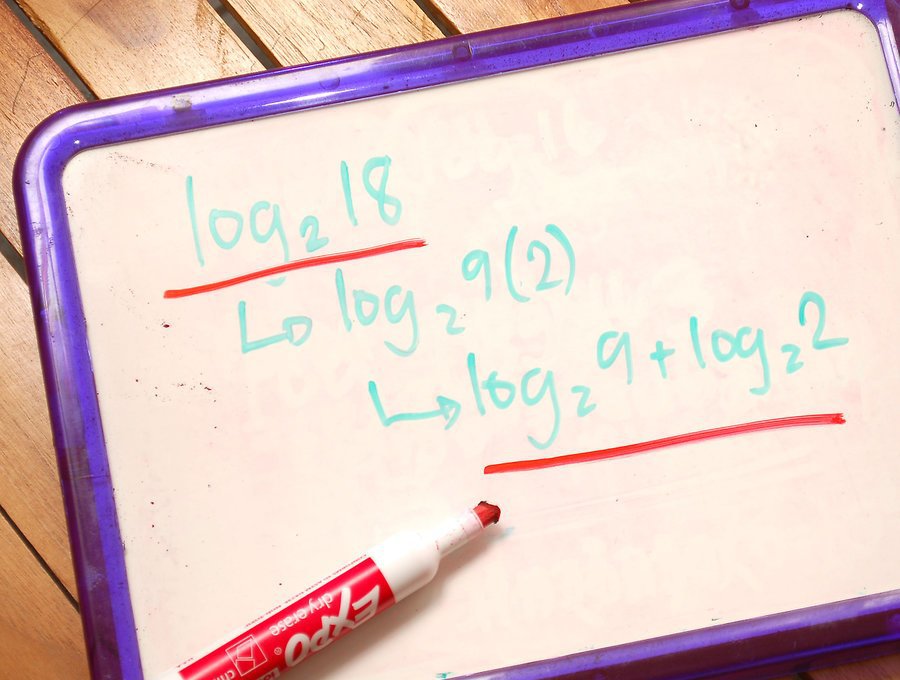
• log _{a ^k} x ^p = (p / k) * log _a x - quindi, se ci sono i gradi nell'argomento e la base del logaritmo, allora possono essere tolti dal segno del logaritmo.
• log _a x = log _{a ^c} x ^c è un caso speciale della regola precedente, quando gli esponenti sono uguali, possono essere ridotti.
• log _a x = (log _b x) (log _b a) è il cosiddetto modulo di transizione, la procedura per convertire il logaritmo in un'altra base.
• log _a x = 1 / log _x a è un caso speciale di transizione, cambio di posizione della base e un dato numero. L'intera espressione, in senso figurato, si rovescia e il logaritmo con la nuova base appare nel denominatore.

Storia dei logaritmi

Nel XVI secolo, fu necessario eseguire molti calcoli approssimativi per risolvere problemi pratici, principalmente in astronomia (per esempio, determinare la posizione di una nave dal Sole o dalle stelle).

Questa necessità è cresciuta rapidamente e notevoli difficoltà hanno creato la moltiplicazione e la divisione di numeri a più cifre. E il matematico matematico Napier decise di sostituire la moltiplicazione laboriosa con l'aggiunta ordinaria per i calcoli trigonometrici, confrontando alcune progressioni per questo. Quindi la divisione, analogamente, viene sostituita da una procedura più semplice e più affidabile - sottrazione, e per estrarre la radice dell'ennesimo grado, è necessario dividere il logaritmo del radicando per n. La soluzione di un compito così difficile in matematica riflette chiaramente gli obiettivi di Naper nella scienza. Ecco come ha scritto su questo all'inizio del suo libro Rabdologiya:

Ho sempre cercato, per quanto mi permettevano i miei poteri e le mie capacità, di liberare le persone dalle difficoltà e dalla noia dei calcoli, la cui pessimistica di solito spaventa molte persone dallo studiare la matematica.

Il nome logaritmo è stato proposto dallo stesso Napier, è stato ottenuto combinando parole greche, che in combinazione significavano "numero di relazioni".

La base del logaritmo è stata introdotta da Spadel. Prese in prestito Eulero dalla teoria dei gradi e trasferito alla teoria dei logaritmi. Il concetto di logaritmismo divenne famoso grazie a Kopp nel 19 ° secolo. E l'uso di logaritmi naturali e decimali, così come le loro designazioni, è apparso grazie a Cauchy.

Nel 1614, John Napier pubblicò in latino un saggio "Descrizione di un incredibile tavolo di logaritmi". C'era una breve descrizione dei logaritmi, delle regole e delle loro proprietà. Quindi il termine "logaritmo" fu stabilito nelle scienze esatte.

L'operazione di logaritmo e la prima menzione di essa apparve grazie a Wallis e Johann Bernoulli, e fu finalmente stabilita da Eulero nel XVIII secolo.

È merito di Eulero estendere la funzione logaritmica della forma y = loga x al dominio complesso. Nella prima metà del XVIII secolo fu pubblicato il suo libro "Introduzione all'analisi dell'infinito", in cui esistevano moderne definizioni di funzioni esponenziali e logaritmiche.

Funzione logaritmica

(имеет смысл, только если: а > 0, а ≠ 1). Una funzione della forma y = log _a x (ha senso solo se: a> 0 e ≠ 1).

• La funzione logaritmica è determinata dall'insieme di tutti i numeri positivi, poiché il registro dei record _a x esiste solo nella condizione - x> 0;.
• Questa funzione può prendere assolutamente tutti i valori dall'insieme di R (numeri reali). Poiché ogni numero reale b ha una x positiva per soddisfare il log di uguaglianza _a x = b, cioè questa equazione ha una radice - x = a ^b (segue dal fatto che log _a a ^b = b).
• La funzione aumenta nell'intervallo a> 0 e diminuisce nell'intervallo 0 <a <1.
• Se a> 0, la funzione assume valori positivi per x> 1.

Va ricordato che qualsiasi grafico della funzione logaritmica y = log _e x ha un punto stazionario (1; 0), poiché log _e 1 = 0. Ciò è chiaramente visibile nell'illustrazione del grafico sottostante.

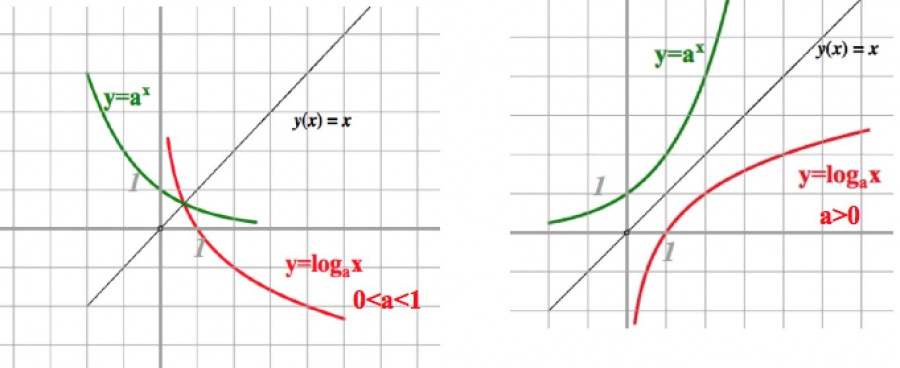
Come vediamo nelle immagini, la funzione non ha uniformità o stranezza, non ha valori più grandi o più piccoli, non è limitata dall'alto o dal basso.

La funzione logaritmica y = log _a x e la funzione esponenziale y = a ^x , dove (a> 0 e ≠ 1), sono reciprocamente inverse. Questo può essere visto nell'immagine dei loro grafici.

Problem solving con logaritmi

Di solito la soluzione di un problema che contiene logaritmi si basa sulla conversione in un modulo standard o ha lo scopo di semplificare le espressioni sotto il segno del logaritmo. O è necessario tradurre i numeri naturali usuali in logaritmi con le basi necessarie, per eseguire ulteriori operazioni per semplificare l'espressione.

Ci sono alcune sottigliezze che non dovrebbero essere dimenticate:

• Quando si risolvono le disuguaglianze, quando entrambe le parti stanno sotto logaritmi secondo la regola con una base, non correre a "scartare" il segno del logaritmo. Ricorda gli intervalli di monotonia della funzione logaritmica. Poiché se la base è maggiore di 1 (nel caso in cui la funzione aumenta) - il segno di disuguaglianza rimane invariato, ma quando la base è maggiore di 0 e minore di 1 (nel caso in cui la funzione diminuisce) - il segno di disuguaglianza cambia al contrario;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Non dimenticare la definizione del logaritmo: log _e x = b, a> 0 e ≠ 1 e x> 0, in modo da non perdere le radici a causa dell'intervallo non registrato di valori validi. Il TLD (range di valori consentito) esiste per quasi tutte le funzioni complesse.

Quando si risolvono le equazioni logaritmiche, si consiglia di utilizzare trasformazioni equivalenti. Inoltre, devi stare attento e prendere in considerazione le possibili trasformazioni che possono portare alla perdita di alcune radici.

Questi sono errori comuni, ma su larga scala che molti hanno incontrato nella ricerca della risposta giusta per l'attività. Non ci sono molte regole per risolvere i logaritmi, quindi questo argomento è più semplice di altri e successivi, ma dovrebbe essere ben compreso.

conclusione

Questo argomento a prima vista può sembrare complicato e macchinoso, ma, esplorandolo sempre più in profondità, inizi a capire che l'argomento finisce e le difficoltà non hanno causato nulla. Abbiamo esaminato tutte le proprietà, le regole e persino gli errori relativi all'argomento dei logaritmi. Successi nell'apprendimento!