Momento di inerzia: formula. Momento di inerzia del corpo
Per cambiare la velocità di movimento del corpo nello spazio, è necessario fare uno sforzo. Questo fatto si applica a tutti i tipi di movimento meccanico ed è associato alla presenza di proprietà inerziali di oggetti aventi una massa. Questo articolo discute la rotazione dei corpi e dà il concetto del loro momento di inerzia.
Qual è la rotazione in termini di fisica?

La risposta a questa domanda può dare a tutti, perché questo processo fisico non è diverso dal suo concetto nella vita di tutti i giorni. Il processo di rotazione è il movimento di un oggetto con una massa finita lungo un percorso circolare attorno ad un asse immaginario. I seguenti esempi di rotazione possono essere forniti:
- Il movimento delle ruote della macchina o della bici.
- La rotazione delle pale di un elicottero o ventilatore.
- Il movimento del nostro pianeta attorno all'asse e intorno al sole.
Quali quantità fisiche caratterizzano il processo di rotazione?
Il movimento circolare è descritto da un insieme di quantità in fisica, le principali delle quali sono elencate di seguito:
- r è la distanza dall'asse del punto materiale di massa m.
- ω e α sono rispettivamente la velocità angolare e l'accelerazione. Il primo valore mostra quanti radianti (gradi) il corpo ruota attorno all'asse in un secondo, il secondo valore descrive il tasso di variazione nel tempo del primo.
- L è il momento angolare, che è simile a una caratteristica simile nel moto lineare.
- Io - il momento di inerzia del corpo. Questo valore è discusso in dettaglio di seguito.
- M è il momento della forza. Caratterizza il grado di cambiamento nel valore di L, se viene applicata una forza esterna.
Queste quantità sono correlate l'una con l'altra dalle seguenti formule di movimento rotatorio:
L = I * ω
M = I * α
La prima formula descrive il movimento circolare del corpo in assenza dell'azione di momenti esterni di forze. Nella forma sopra, riflette la legge di conservazione del momento angolare L. La seconda espressione descrive il caso di accelerazione o decelerazione della rotazione del corpo come risultato dell'azione del momento di forza M. Entrambe le espressioni sono spesso utilizzate quando si risolvono problemi di dinamica lungo una traiettoria circolare.
Ad
Come si può vedere da queste formule, il momento di inerzia attorno all'asse (I) in esse viene usato come un certo coefficiente. Consideriamo questo valore in maggiore dettaglio.
Da dove viene il valore di I?
In questa sezione consideriamo l'esempio di rotazione più semplice: un movimento circolare di un punto materiale di massa m, la cui distanza dall'asse di rotazione è r. Questa situazione è mostrata nella figura.
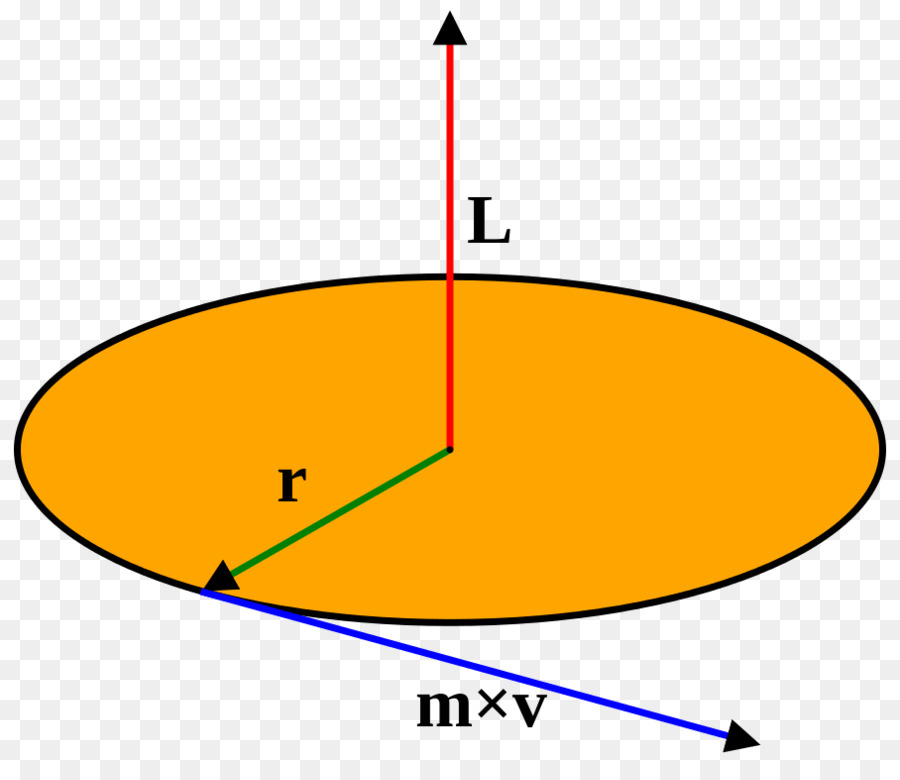
Secondo la definizione, il momento angolare L è scritto come il prodotto della spalla r dai punti p dell'impulso lineare:
L = r * p = r * m * v, poiché p = m * v
Dato che la velocità lineare e angolare sono legate l'una all'altra attraverso la distanza r, questa uguaglianza può essere riscritta come:
v = ω * r => L = m * r 2 * ω
Il prodotto della massa di un punto materiale per il quadrato della distanza dall'asse di rotazione è chiamato momento d'inerzia. La formula sopra riportata verrà riscritta in questo caso come segue:
I = m * r 2 => L = I * ω
Cioè, abbiamo ricevuto l'espressione che è stata data nel paragrafo precedente e ho introdotto il valore di I.
La formula generale per la dimensione del corpo I
L'espressione per il momento di inerzia con massa m di un punto materiale è fondamentale, cioè consente di calcolare questo valore per qualsiasi corpo avente una forma arbitraria e una distribuzione di massa non uniforme in esso. Per fare ciò, è necessario dividere l'oggetto preso in considerazione in piccoli elementi di massa m i (intero I è il numero dell'elemento), quindi moltiplicare ciascuno di essi per il quadrato della distanza r i 2 rispetto all'asse attorno al quale viene considerata la rotazione e aggiungere i risultati. Il metodo descritto per trovare il valore di I può essere scritto matematicamente come segue:
Ad
I = Σ i (m i * r i 2 )
Se il corpo è diviso in modo tale che io-> ∞, allora la somma data viene sostituita da un integrale sulla massa del corpo m:
I = ∫ m (r i 2 * dm)
Questo integrale è equivalente a un altro integrale sul volume del corpo V, perché dV = ρ * dm:
I = ρ * ∫ V (r i 2 * dV)
Tutte e tre le formule sono utilizzate per calcolare il momento di inerzia del corpo. In questo caso, nel caso di una distribuzione di massa discreta nel sistema, è preferibile utilizzare la prima espressione. Con una distribuzione continua di massa, applica la 3a espressione.
Proprietà di I e il suo significato fisico
La procedura descritta per ottenere un'espressione generale per I ci consente di trarre alcune conclusioni sulle proprietà di questa quantità fisica:
- è additivo, cioè il momento totale di inerzia del sistema può essere rappresentato come la somma dei momenti delle sue singole parti;
- dipende dalla distribuzione di massa all'interno del sistema, così come dalla distanza dall'asse di rotazione, più grande è quest'ultimo, il più grande io;
- non dipende dalle forze M che agiscono sul sistema dei momenti e sulla velocità di rotazione ω.

Il significato fisico di I è quanto fortemente il sistema impedisce qualsiasi cambiamento nella sua velocità di rotazione, cioè il momento di inerzia caratterizza il grado di "levigatezza" delle accelerazioni risultanti. Ad esempio, una ruota di bicicletta può essere facilmente ruotata a velocità angolari elevate ed è anche facile da arrestare, ma per cambiare la rotazione del volano sull'albero a gomiti di un'automobile, ci vorrà uno sforzo considerevole e un po 'di tempo. Nel primo caso, c'è un sistema con un piccolo momento di inerzia, nel secondo - con un grande.
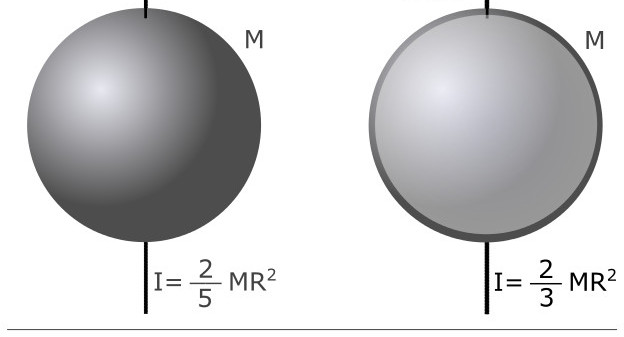
Il valore di I di alcuni corpi per l'asse di rotazione che passa attraverso il centro di massa
Se applichiamo l'integrazione sul volume per qualsiasi corpo con una distribuzione di massa arbitraria, allora possiamo ottenere la quantità I. Per oggetti omogenei che hanno una forma geometrica ideale, questo problema è già stato risolto. Le formule per il momento di inerzia per una verga, un disco e una sfera di massa m, in cui la loro materia costitutiva è uniformemente distribuita, sono indicate di seguito:
- Il nucleo L'asse di rotazione è perpendicolare ad esso. I = m * L 2/12, dove L è la lunghezza dell'asta.
- Disco di spessore arbitrario. Il momento di inerzia con l'asse di rotazione, che passa perpendicolarmente al suo piano attraverso il centro di massa, viene calcolato come segue: I = m * R 2/2, dove R è il raggio del disco.
- Ball. In considerazione dell'elevata simmetria di questa figura, per qualsiasi posizione dell'asse che passa attraverso il suo centro, I = 2/5 * m * R2, qui R è il raggio della sfera.
Di seguito vengono forniti due esempi di risoluzione dei problemi per l'applicazione della formula generale per il calcolo di I e per l'utilizzo della proprietà di additività di questa quantità.
Il compito di calcolare il valore di I per un sistema con una distribuzione di massa discreta
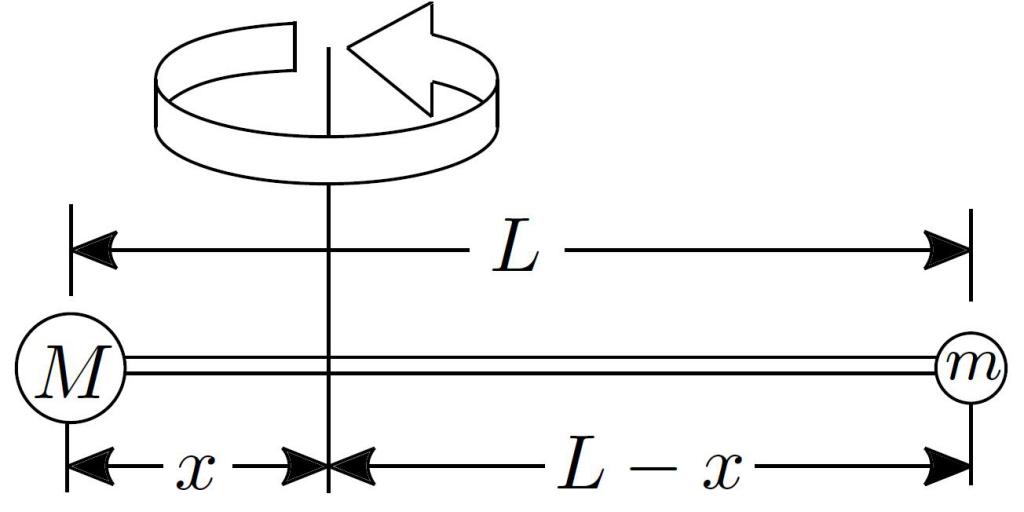
Immagina una canna lunga 0,5 metri, fatta di un materiale duro e leggero. Questa asta è fissata sull'asse in modo tale da essere perpendicolare esattamente al centro. Tre pesi sono sospesi su questa asta come segue: su un lato dell'asse ci sono due pesi del peso di 2 kg e 3 kg, situati rispettivamente a distanze di 10 cm e 20 cm dalla sua estremità; d'altra parte, un singolo peso di 1,5 kg è sospeso all'estremità dell'asta. Per questo sistema, è necessario calcolare il momento di inerzia I e determinare a quale velocità ω la barra ruoterà se una forza di 50 N viene applicata a una delle sue estremità per 10 secondi.
Poiché la massa della barra può essere trascurata, è necessario calcolare il momento I per ogni carico e aggiungere i risultati ottenuti per ottenere il momento completo del sistema. Secondo la condizione del compito, dall'asse un peso di 2 kg è a una distanza di 0,15 m (0,25-0,1), un carico di 3 kg è 0,05 m (0,25-0,20), un carico di 1,5 kg è 0,25 m Utilizzando la formula per il momento del punto materiale I, otteniamo:
Ad
I = I 1 + I 2 + I 3 = m 1 * r 1 2 + m 2 * r 2 2 + m 3 * r 3 2 = 2 * (0,15) 2 + 3 * (0,05) 2 + 1,5 * (0,25) 2 = 0,14 625 kg * m 2 .
Si noti che nell'esecuzione dei calcoli, tutte le unità di misura sono state trasferite al sistema SI.
Per determinare la velocità angolare di rotazione dell'asta dopo l'azione della forza, dovresti applicare la formula con il momento di forza, che è stato dato nel secondo paragrafo dell'articolo:
M = I * α
Poiché α = Δω / Δt e M = r * F, dove r è la lunghezza della spalla, otteniamo:
r * F = I * Δω / Δt => Δω = r * F * Δt / I
Dato che r = 0,25 m, sostituiamo i numeri nella formula, otteniamo:
Δω = r * F * Δt / I = 0,25 * 50 * 10 / 0,14625 = 854,7 rad / s
Il valore risultante è abbastanza grande. Per ottenere la solita velocità, dovresti dividere Δω per 2 * pi radianti:
f = Δω / (2 * pi) = 854.7 / (2 * 3.1416) = 136 s -1
Quindi, la forza applicata F all'estremità della barra con pesi in 10 secondi lo farà ruotare ad una frequenza di 136 giri al secondo.
Il calcolo del valore di I per l'asta, quando l'asse passa attraverso la sua estremità
Lasciare che ci sia una verga omogenea di massa m e lunghezza L. È necessario determinare il momento di inerzia, se l'asse di rotazione si trova all'estremità dell'asta perpendicolare ad esso.
Ad
Usiamo l'espressione generale per I:
I = ρ * ∫ V (r i 2 * dV)
Scoprendo l'oggetto preso in considerazione in volumi elementari, notiamo che dV può essere scritto come dr * S, dove S è l'area della sezione della barra, e dr è lo spessore dell'elemento di divisione. Sostituendo questa espressione nella formula, abbiamo:
I = ρ * S * ∫ L (r 2 * dr)
Questo integrale è abbastanza semplice da calcolare, otteniamo:
I = ρ * S * (r 3/3) | 0 L => I = ρ * S * L 3/3
Poiché il volume dell'asta è S * L, e la massa è ρ * S * L, allora otteniamo la formula finale:
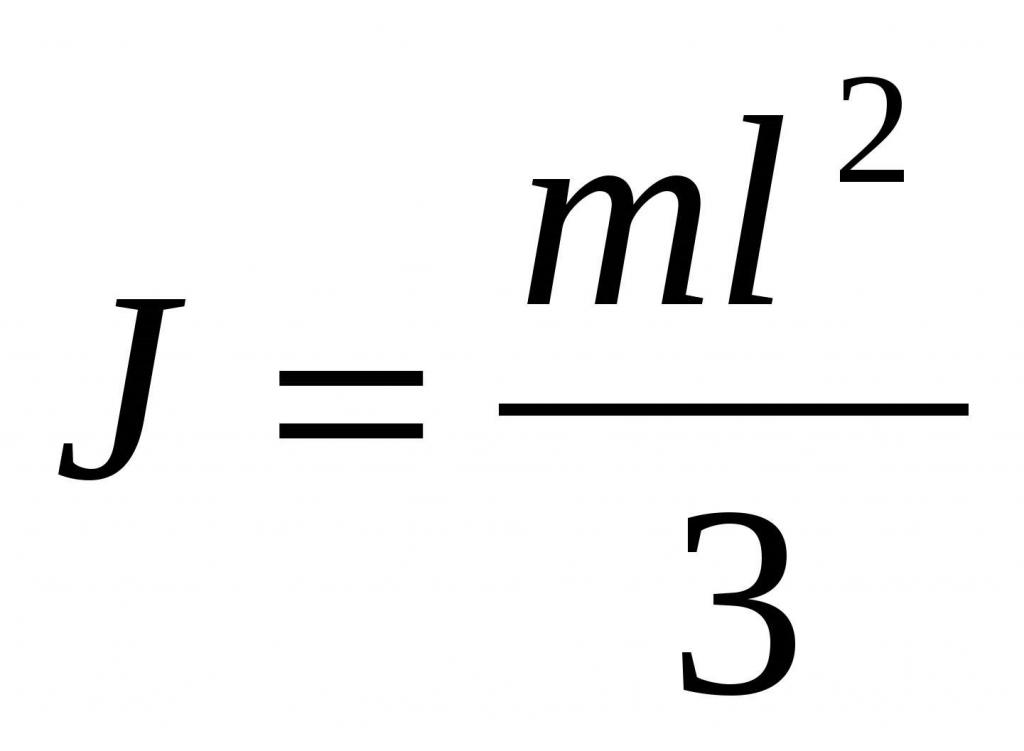
È interessante notare che il momento di inerzia per la stessa asta, quando l'asse passa attraverso il suo centro di massa, è 4 volte inferiore al valore ottenuto (m * L 2/3 / (m * L 2/12) = 4).