Ostrogradsky - Teorema di Gauss e formula
MV Ostrogradsky - Matematico e fisico russo dall'Impero russo, accademico. Ha dato un enorme contributo allo sviluppo analisi matematica teoria della probabilità, meccanica (sezione della fisica) teoria dei numeri. Nel 1826, ha derivato una formula, ora chiamata la formula di Ostrogradsky-Gauss.
Storia della scoperta
La formula di Ostrogradsky-Gauss fu menzionata per la prima volta da Joseph Lagrange nel 1762.
Inoltre, il metodo principale per ridurre l'integrale triplo alla superficie è stato dimostrato da Karl Gauss, che ha usato la soluzione dei problemi dell'elettrodinamica come base per la dimostrazione. È successo nella prima metà del XIX secolo.
Inoltre, la formula in forma generale è stata presentata da Mikhail Ostrogradsky. Con il suo aiuto, è diventato possibile esprimere il valore del differenziale in un parametro dall'integrale N-times.
Il significato della formula Ostrogradsky
La formula di Ostrogradsky-Gauss mette in relazione l'integrale triplo rispetto al volume spaziale con l'integrale sulla superficie della sua faccia. È un analogo della formula verde, che mette in relazione un doppio integrale su un piano con un curvilineo lungo i suoi confini.
Ad
Derivazione della formula
Ostrogradsky - formula di Gauss: conclusione. Supponiamo che nel dominio W sia definita la funzione integranda R (x, y, z), che è definita e continua. Il suo derivato è simile nell'intero dominio W, compreso il suo confine. In questa forma, il teorema di Ostrogradsky - Gauss è ora noto (la formula è riportata di seguito).
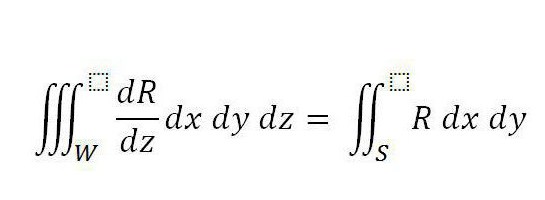
Inoltre, S è la superficie che delimita il corpo e l'integrale sulla destra è distribuito sul suo lato esterno.
E assolutamente vero
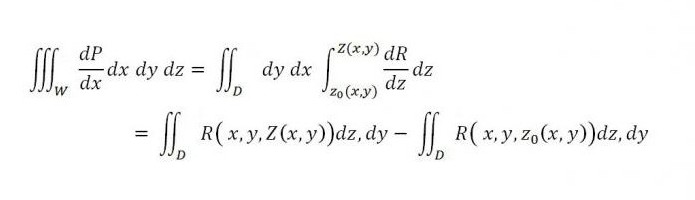
Se consideriamo allo stesso modo gli integrali sulla superficie, allora
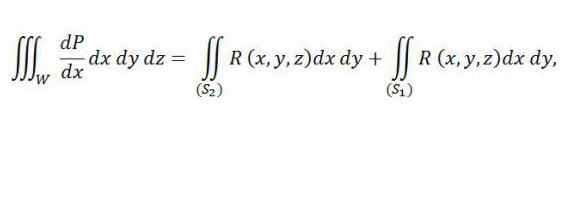
mentre a destra è la somma di due integrali - il primo è relativo alla parte superiore della superficie (S 2 ), e il secondo - alla parte inferiore della superficie (S 1 ). Se aggiungiamo l'integrale indicato di seguito a questa uguaglianza a destra, la sua validità non sarà violata:
Ad
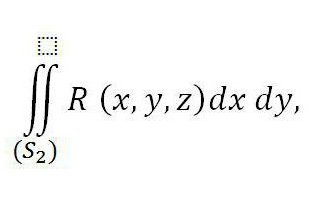
Corrisponde alla parte esterna della superficie S 3 a causa dell'uguaglianza a zero.
Se combiniamo tutti e tre gli integrali di cui sopra in uno, otteniamo un caso speciale della formula Ostrogradsky.
È facile rendersi conto che questa formula è vera per una più ampia classe di corpi ed è valida anche per le figure delimitate da assolutamente qualsiasi superficie non lineare.
Le seguenti formule sono similmente vere:
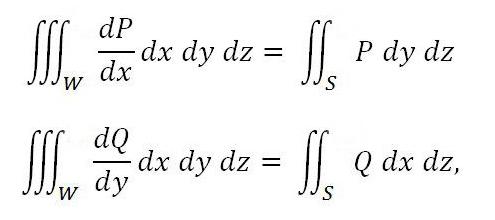
se le funzioni Q e P sono continue nel dominio insieme alle loro derivate dP / dx e dQ / dy.
Se aggiungiamo entrambe le uguaglianze, otteniamo l'espressione per la formula Ostrogradsky. Visualizza l'integrale sulla superficie, correlato con la parte esterna della superficie, attraverso l'integrale triplo, che viene rilevato sul corpo stesso, il cui limite è la superficie sopra menzionata.
Dovrebbe essere compreso che le formule di Green, Stokes e Ostrogradsky esprimono l'integrale associato a un certo corpo geometrico, attraverso un integrale che viene preso sul suo confine. La formula di Green viene utilizzata solo nel caso di bidimensionalità dello spazio, la formula di Stokes viene applicata allo spazio bidimensionale curvo.
La formula di Newton-Leibniz può anche essere considerata come un analogo di queste formule, ma per uno spazio unidimensionale.
L'uso di questa formula
Lasciate che le funzioni continue A, B e C siano date in qualsiasi regione di spazio non chiusa. Prendendo qualsiasi superficie chiusa che si trova in una data regione e delimitando un certo corpo, possiamo considerare il seguente integrale sulla superficie:
Ad
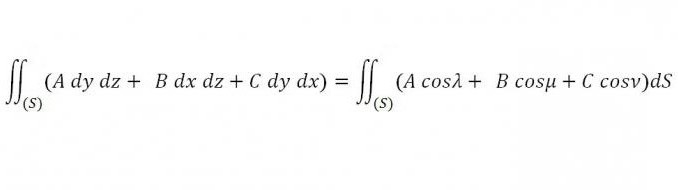
È necessario trovare tali valori di A, B e C in modo tale che per ogni x, y e z questo integrale sia uguale a zero.
Per fare ciò, utilizzare la formula di Ostrogradsky-Gauss. Una delle condizioni implicite è la certezza e la continuità delle funzioni A, B e C e dei loro derivati.
È anche richiesto di introdurre specificatamente la restrizione più indicata per un dato caso: sia il corpo che il contorno della superficie devono essere contenuti simultaneamente in un'area specifica e specificata, chiamata semplicemente connessa. La sua caratteristica principale è l'assenza di spazio vuoto (incluso lo spazio dei punti). Quindi, il confine del corpo sarà uno e con quello una singola superficie.
Dopo aver applicato la formula, è possibile ottenere la seguente condizione, che è sufficiente:
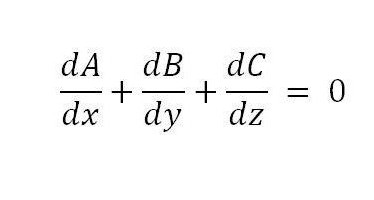
Per dimostrare che la condizione è anche necessaria, è sufficiente utilizzare la differenziazione dell'integrale triplo.
In conclusione, è necessario dire sulle aree di utilizzo.
Come si usa la formula Ostrogradsky-Gauss nella pratica? Esempi di utilizzo possono essere trovati in vari campi: per ricavare alcune formule in fisica (ad esempio, l'equazione di diffusione), trasformare gli integrali, calcolare gli integrali di Gauss, provare alcune formule e molto altro.