Proprietà e formule di un prisma rettangolare

Un prisma è una delle figure volumetriche perfette, insieme a una palla, un cilindro e una piramide, le cui proprietà sono discusse in una sezione speciale di geometria - stereometria. In questo articolo discutiamo le caratteristiche principali di un prisma rettangolare.

Figura del prisma

Molte persone conoscono prismi triangolari o esagonali, ma non tutti hanno un'idea chiara di ciò che questa figura è in generale. In geometria, sotto esso capisce un oggetto spaziale che è delimitato da due poligoni identici e diversi quadrangoli. Due poligoni sono chiamati basi del prisma. Si trovano su piani paralleli. Tutti i quadrilateri sono parallelogrammi e formano la superficie laterale della figura.

Le principali formule e proprietà di un prisma riguardano i problemi di determinazione del volume, l'area della sua superficie e il numero di elementi che formano la figura. La composizione di quest'ultimo include vertici, bordi e facce. Le quantità di questi elementi sono collegate tra loro dall'espressione di Eulero per i poliedri. Ha la seguente forma:

Numero di fronti = numero di facce + numero di vertici - 2

Poiché la superficie laterale di un prisma è sempre rappresentata da parallelogrammi, le sue caratteristiche principali dipendono dal tipo di poligono che giace nelle basi di questa figura. Se il poligono è un triangolo, il prisma viene chiamato triangolare, se il quadrilatero è quadrangolare e così via.

Prisma rettangolare

Se l'angolo tra ciascun lato del prisma e la sua base è 90 ^° , allora tale figura è chiamata rettangolare. Si noti che stiamo parlando dell'angolo tra i lati, e non tra le costole. Spesso una tale figura è chiamata un prisma diretto.

Quando l'angolo marcato è 90 ^o , tutti i parallelogrammi diventano automaticamente rettangoli. Questo è un altro motivo per cui questo prisma è chiamato rettangolare. La figura seguente mostra come si presenta un prisma rettangolare.

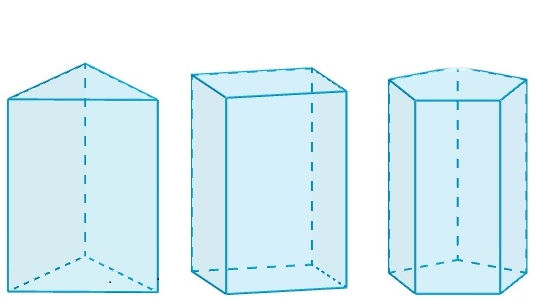
Qui vediamo che ciascuno dei tre prismi è diverso dagli altri dal tipo di poligono sottostante alla forma. La figura mostra prismi triangolari, quadrangolari e pentagonali. Il numero di rettangoli per ciascuno di essi è 3, 4 e 5, rispettivamente.

Una proprietà importante di un prisma rettangolare, che la distingue da un angolo obliquo, è il fatto che la lunghezza del suo bordo laterale coincide con l'altezza della figura. Questa proprietà è molto comoda per il calcolo della superficie e del volume.

Prisma corretto

Ogni prisma diretto alla base del quale si trova un poligono regolare è definito regolare. Il poligono specificato deve avere la stessa lunghezza di tutti i lati e angoli uguali. Tale rettangolo è un triangolo equilatero, quadrato, pentagono e così via.

La figura seguente mostra due prismi. Quello di sinistra è corretto, perché alla sua base c'è un quadrato ed è dritto. Quella giusta, nonostante il fatto che la linea sia diritta, non è corretta, poiché la sua base è un quadrilatero arbitrario.

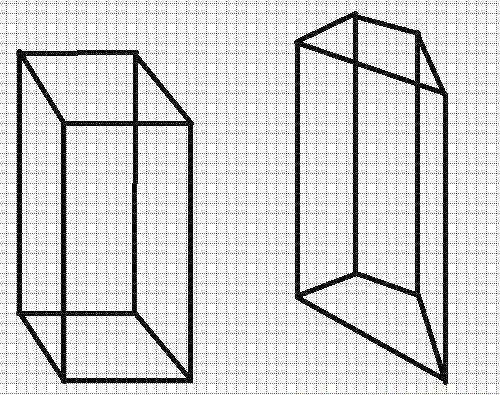
L'unico prisma corretto che ha il suo nome è un cubo. Si ottiene quando l'altezza della figura coincide con la lunghezza del lato del quadrato alla base.

Poiché l'area per un poligono regolare è facile da calcolare, quindi per qualsiasi prisma regolare, sono note le formule relative alla sua area superficiale e al suo volume.

Area del poligono regolare

Prima di dare le formule per l'area della superficie e il volume di un prisma rettangolare, considera un poligono regolare.

La figura seguente mostra un insieme di poligoni regolari, ad eccezione di un cerchio.

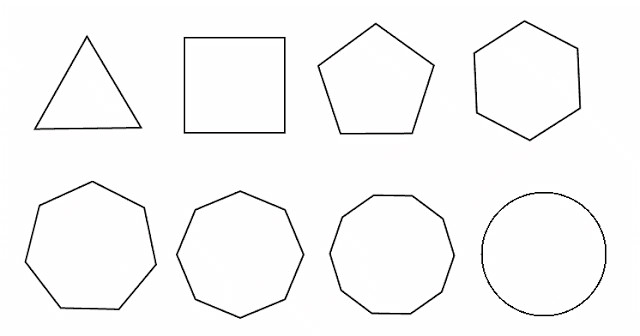
Si vede che per ciascuno di essi il numero di lati coincide con il numero di angoli. Inoltre, tutti i lati e gli angoli sono uguali. Queste proprietà ci permettono di dare una formula che è universale per tutti i poligoni regolari e ci permette di calcolare la loro area. La formula ha la forma:

S _n = n / 4 * a ² * ctg (pi / n)

Dove a è la lunghezza del lato, n è il numero di lati (vertici) della forma. Il simbolo ctg indica la funzione trigonometrica cotangente.

Mostriamo come utilizzare questa espressione. Ad esempio, calcoliamo l'area di un triangolo equilatero. Per lui n = 3, quindi:

S ₃ = 3/4 * a ² * ctg (pi / 3) = 3/4 * a ² * 1 / √3 = √ 3/4 * a ²

Ora usa questa formula per il quadrato. Abbiamo:

S ₄ = 4/4 * a ² * ctg (pi / 4) = a ² * 1 = a ²

Cioè, abbiamo la ben nota espressione per il quadrato del quadrato.

Superficie del prisma

Quando è stata data una definizione geometrica della figura in questione, è stato dimostrato che consiste di due basi e un numero di parallelogrammi. Questo numero è esattamente uguale al numero di lati del poligono alla base. L'area della figura considerata può essere annotata con la seguente formula:

S = 2 * S _o + S _b

Dove S _o - area di base, S _b - superficie laterale. Poiché quest'ultimo è costituito da n parallelogrammi, il suo valore è uguale alla somma delle loro aree.

Nel caso di un prisma rettilineo regolare, la superficie laterale sarà formata da rettangoli con i lati aeh, dove a è la lunghezza del lato di base, h è l'altezza del prisma. Per il caso di n quadrato regolare, otteniamo la formula per l'area S _{tot del} prisma:

S _tot = n / 2 * a ² * ctg (pi / n) + n * a * h

La figura seguente mostra una scansione di un prisma esagonale.

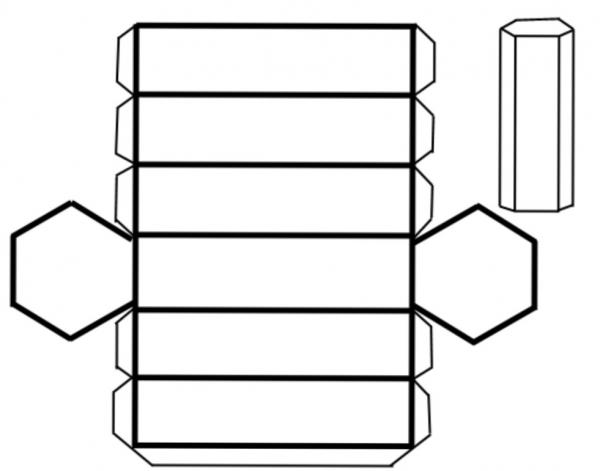
Si può vedere che la figura è formata da due esagoni regolari e sei rettangoli identici, un lato dei quali è uguale al lato dell'esagono. Applicando l'espressione sopra per questo prisma, otteniamo:

S ⁶ _tot = _6/2 * a ² * ctg (pi / 6) + 6 * a * h = 3 * a * (√3 * a + 2 * h)

Formula del volume

Il volume del prisma viene generalmente calcolato utilizzando la seguente formula semplice:

V = S _o * h

Per una forma rettangolare, l'altezza è il suo bordo, quindi questa espressione è facile da applicare. Ad esempio, calcoliamo il volume per un prisma triangolare regolare. L'area della sua base è già stata calcolata, è uguale a:

S ₃ = √3 / 4 * a ²

Quindi il valore del volume per la forma sarà il seguente:

V = S ₃ * h = √3 / 4 * a ² * h

Le precedenti formule per un prisma dritto con un poligono regolare alla base mostrano che tutte le proprietà di tali figure possono essere ottenute se si conoscono solo due parametri: la lunghezza del lato del n-gon e l'altezza del prisma.