Il corpo è stato lanciato con un angolo verso l'orizzonte: velocità, raggio e altezza

In questo articolo analizzeremo la situazione in cui il corpo è stato lanciato in un angolo rispetto all'orizzonte. Questo potrebbe essere un tiro di pietra con una mano, un colpo da un cannone, il lancio di una freccia da un arco e così via. Tutte le situazioni menzionate sono descritte allo stesso modo da un punto di vista matematico.

Caratteristica del movimento ad angolo rispetto all'orizzonte

Quali sono le somiglianze degli esempi sopra riportati dal punto di vista della fisica? Si trova nella natura delle forze che agiscono sul corpo. Durante il volo libero di un certo corpo, solo due forze agiscono su di esso:

• Gravity.
• Resistenza all'aria

Se il peso corporeo è abbastanza grande e la sua forma è puntata (proiettile, freccia), allora la resistenza aerea può essere trascurata.

Pertanto, il movimento di un oggetto proiettato in un angolo rispetto all'orizzonte del corpo è un compito in cui appare solo la forza di gravità. Questo è ciò che determina la forma della traiettoria, che è descritta con buona precisione da una funzione parabolica.

Equazioni del moto lungo una traiettoria parabolica. Velocità di

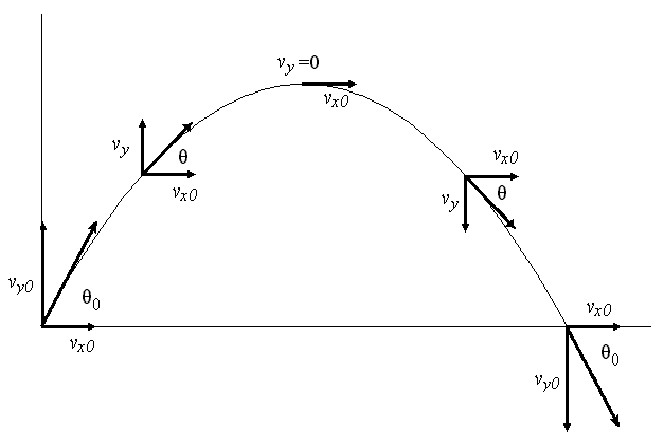
Il corpo è lanciato in un angolo verso l'orizzonte. Come puoi descrivere il suo movimento? Poiché l'unica forza che agisce durante il volo di un corpo è diretta verso il basso, la sua componente orizzontale è zero. Questo fatto significa che il movimento orizzontale di un oggetto è determinato in modo univoco dalle condizioni iniziali (angolo di lancio o tiro θ e velocità v). Il movimento verticale del corpo è un vivido esempio di movimento uniformemente accelerato, in cui la costante g svolge un ruolo nell'accelerazione (9,81 m / s ² ).

Considerato quanto sopra, possiamo scrivere due componenti per la velocità di un corpo volante al tempo t:

v _x = v * cos (θ);

v _y = v * sin (θ) - g * t

Come si può vedere, il componente v _x non dipende dal tempo e rimane costante durante l'intera traiettoria di volo (a causa dell'assenza di forze esterne nella direzione dell'asse x). Il componente v ha un massimo nel momento iniziale. E poi inizia a diminuire, fino al punto che svanisce nel punto massimo di decollo del corpo. Dopo di ciò, cambia il suo segno e al momento della caduta risulta essere uguale al modulo della componente iniziale v _y , cioè v * sin (θ).

Le equazioni scritte ci permettono di determinare la velocità di un corpo proiettato con un angolo verso l'orizzonte in qualsiasi momento t. Il suo modulo sarà uguale a:

v = √ (v _x ² + v _y ² ) = √ (v ² * cos ² (θ) + v ² * sin ² (θ) - 2 * v * sin (θ) * g * t + g ² * t ² ) =

= √ (v ² - 2 * v * sin (θ) * g * t + g ² * t ² )

Equazioni del moto lungo una traiettoria parabolica. Intervallo di volo

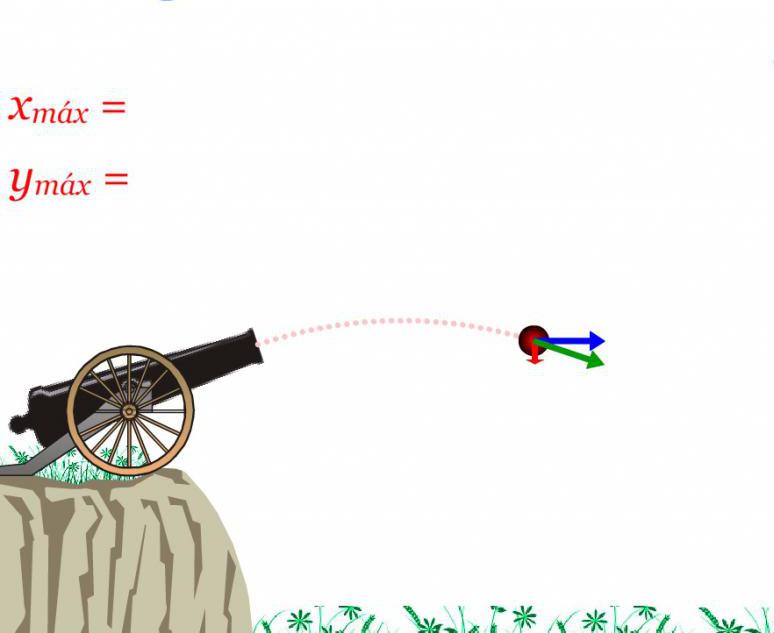
Il corpo è lanciato in un angolo verso l'orizzonte. Che distanza volerà? La questione della gamma di volo riguarda il cambiamento della coordinata x. È possibile trovare questo valore se integriamo entrambe le componenti della velocità nel tempo. Come risultato dell'integrazione, otteniamo le formule:

x = v * cos (θ) * t + x ₀ ;

y = v * sin (θ) * t - g * t 2/2 + y ₀

La differenza tra le coordinate x e x ₀ è l'intervallo. Se assumiamo che x ₀ = 0, allora l'intervallo sarà uguale a x, per scoprire quale è necessario sapere per quanto tempo il corpo sarà nell'aria.

La seconda equazione consente di calcolare questo tempo, a condizione che il valore di y _{0 sia} noto (altezza h, da cui viene lanciato il corpo). Quando l'oggetto completa il suo movimento (cade a terra), la sua coordinata y diventerà zero. Calcola l'ora in cui ciò accade. Abbiamo:

v * sin (θ) * t - g * t 2/2 + h = 0

Davanti a noi c'è un'uguaglianza quadrata completa. Lo risolviamo attraverso la discriminante:

D = v ² * sin ² (θ) - 4 * (-g / 2) * h = v ² * sin ² (θ) + 2 * g * h;

t = (-v * sin (θ) ± √D) / (2 * (-g / 2))

Rifiutiamo la radice negativa. Otteniamo il seguente orario di volo:

t = (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Ora sostituiamo questo valore in uguaglianza per l'intervallo di volo. Otteniamo:

x = v * cos (θ) * (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Se il corpo viene gettato da terra, cioè h = 0, allora questa formula sarà molto più semplice. E prendi la forma:

x = 2 * v ² * cos (θ) * sin (θ) / g = v ² * sin (2 * θ) / g

L'ultima espressione è stata ottenuta utilizzando la connessione tra le funzioni trigonometriche di seno e coseno (formula di riduzione).

Dato che il seno ha un valore massimo per un angolo retto, allora il raggio massimo viene raggiunto quando il corpo viene gettato (sparato) da terra con un angolo di 45 °, e questo range è uguale a:

x = v ² / g

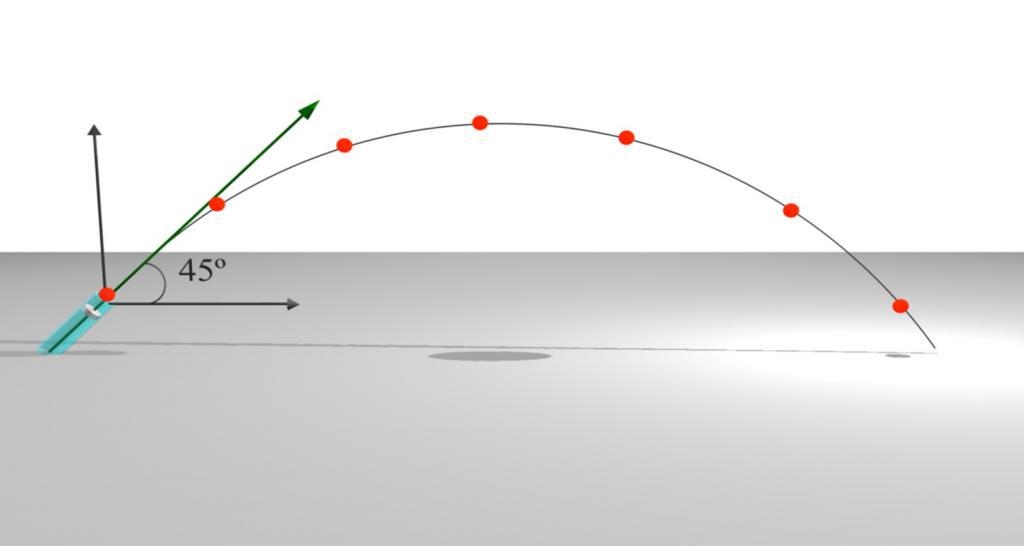
L'altezza del corpo, proiettata in un angolo verso l'orizzonte

Ora definiamo un altro parametro importante: l'altezza a cui un oggetto abbandonato è in grado di arrampicarsi. Ovviamente, per fare ciò, è sufficiente considerare solo un cambiamento nella coordinata y.

Quindi, il corpo fu gettato in un angolo verso l'orizzonte, a quale altezza sarebbe decollato? Questa altezza corrisponderà all'uguaglianza a zero della componente di velocità v _y . Abbiamo l'equazione:

v _y = v * sin (θ) - g * t = 0

Risolvi l'equazione. Otteniamo:

t = v * sin (θ) / g

Ora dovresti sostituire questa volta nell'espressione per la coordinata y. Otteniamo:

y = v * sin (θ) * t - g * t 2/2 + h = v ² * sin ² (θ) / g - g / 2 * v ² * sin ² (θ) / g ² + h =

= v ² * sin ² (θ) / (2 * g) + h

Questa formula suggerisce che l'altitudine massima, al contrario del raggio di volo, si ottiene lanciando il corpo verticalmente (θ = 90). In questo caso, arriviamo alla formula:

y = v ² / (2 * g) + h

È curioso notare che in tutte le formule fornite in questo articolo la massa corporea non appare. Le caratteristiche di una traiettoria parabolica sono indipendenti da essa, ma solo in assenza di resistenza aerea.