Il concetto di accelerazione. Moto con accelerazione costante. Formule e compiti di esempio
La cinematica è una sezione della meccanica del movimento in fisica che si occupa dello studio e della descrizione del movimento dei corpi. Questo articolo presenta i valori di base che descrivono il movimento meccanico. Consideriamo quali accelerazioni e movimenti sono con accelerazione costante, presentiamo le formule corrispondenti.
Tre cinematiche
Questi valori sono il percorso L, la velocità v¯ e l'accelerazione a¯. Il primo è uno scalare ed è misurato in metri, il secondo e il terzo sono valori vettoriali, che sono espressi in metri al secondo e in metri per secondo quadrato, rispettivamente. Tutte le unità corrispondono al sistema SI.
Secondo la definizione, la velocità è la velocità di movimento del corpo nello spazio, cioè:
v¯ = dL / dt
A sua volta, l'accelerazione è il tasso di cambio di velocità, che è matematicamente registrato come:
a¯ = dv¯ / dt
Ha senso considerare le caratteristiche cinematiche in riferimento a una data traiettoria di movimento. Quest'ultimo può essere rettilineo o curvilineo. La direzione della piena accelerazione dipende dal tipo di traiettoria. La velocità è diretta alla traiettoria è sempre tangenziale.
Ad
Caratteristiche di accelerazione durante la guida su una curva
Poiché l'accelerazione è una caratteristica numerica di un cambiamento di velocità, descrive in modo univoco tutti gli aspetti di questo cambiamento. Stiamo parlando non solo del valore assoluto, ma anche del vettore di direzione v¯. Un cambiamento nella grandezza della velocità descrive l'accelerazione tangenziale o tangenziale. È diretto contro il vettore di velocità o contro di esso. La formula per il suo calcolo è:
a t = dv / dt
Quando il corpo si muove in una curva, ad esempio, in un cerchio, il valore di v ¯ cambia continuamente direzione. Qual è la ragione di questo cambiamento? Consiste nell'azione sul corpo dell'accelerazione normale o centripeta. Questo valore è diretto perpendicolare alla linea di traiettoria e viene calcolato dalla formula:
Ad
a n = v 2 / r
Dove v è il valore assoluto della velocità, r è la curvatura della traiettoria (raggio del cerchio).
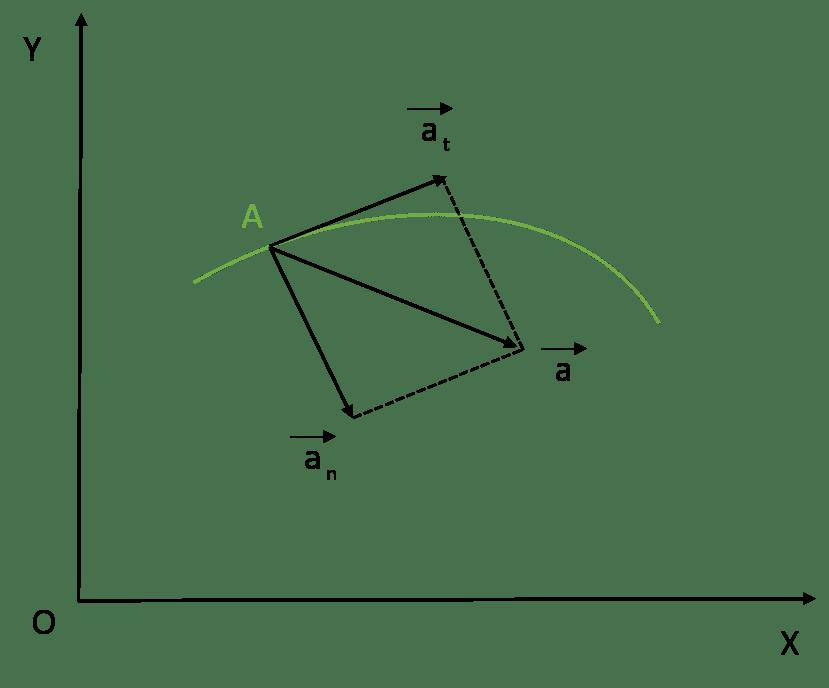
Entrambe le componenti della piena accelerazione ci permettono di determinarlo usando questa uguaglianza:
a = √ (a t 2 + a n 2 )
Si noti che il movimento lungo un percorso curvo implica sempre che il corpo abbia due componenti di accelerazione.
Moto con accelerazione costante in linea retta
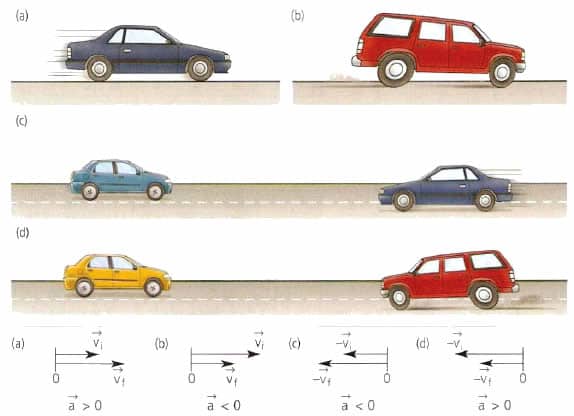
Se la traiettoria è una linea retta, lo studio del processo di movimento è notevolmente facilitato. Il fatto è che con un tale movimento, la velocità è sempre diretta in una direzione, il che significa che il componente normale di accelerazione è assente. L'accelerazione completa con movimento rettilineo è determinata in modo univoco dalla sua componente tangenziale. Più avanti nell'articolo considereremo solo il movimento lungo una linea retta, quindi la quantità a sarà chiamata semplicemente accelerazione.
Particolare attenzione dovrebbe essere prestata al processo di spostamento del corpo in linea retta, che viene effettuato con accelerazione costante. Per una tale mossa, scrivi semplicemente le equazioni matematiche del movimento. Saranno discussi di seguito.
Esempi del movimento di corpi con accelerazione costante sono l'accelerazione della macchina dall'inizio, la caduta libera dei corpi in un campo gravitazionale uniforme e la frenata dei veicoli.
Formule per la velocità
Considerando l'accelerazione e il movimento con accelerazione costante nel 10 ° grado delle scuole secondarie, gli studenti imparano le formule per determinare la velocità e la distanza percorsa. Iniziamo con le formule per la velocità.
Ad
Supponiamo che il corpo fosse a riposo, quindi iniziò a muoversi con un'accelerazione costante. Come cambierà la sua velocità? La risposta a questa domanda contiene la seguente uguaglianza:
v = a * t
Cioè, la velocità aumenterà linearmente. Il coefficiente di proporzionalità tra i valori di v e t è l'accelerazione a.
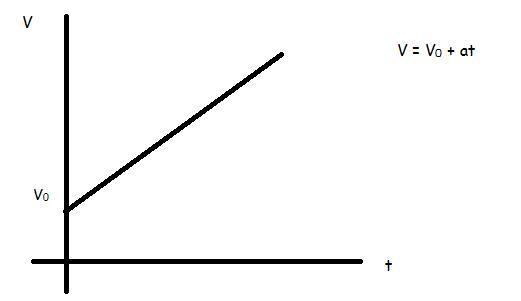
Ora immagina una situazione in cui il corpo si muove ad una velocità costante v 0 , e poi inizia ad accelerare. Come cambierà la precedente formula per la velocità? Sembrerà:
v = v 0 + a * t.
Si noti che il conto alla rovescia del tempo in questa formula inizia dal momento in cui l'accelerazione appare nel corpo.
Supponiamo ora la terza opzione: invece di accelerare il movimento nell'esempio precedente, il corpo ha iniziato a rallentare. In questa situazione, usa l'espressione:
v = v 0 - a * t.
In tutti e tre i casi, i grafici della velocità rispetto al tempo sono linee rette.
Formule per il percorso
Considerando il tema dell'accelerazione e del movimento con una costante accelerazione in linea retta, è anche necessario presentare le formule per il percorso percorso dal corpo. In definitiva, in pratica, è questa quantità cinematica che ha senso.
Le formule corrispondenti per L possono essere ottenute se prendiamo l'integrale nel tempo per le espressioni di cui sopra per le velocità. Di seguito sono riportate tre formule:
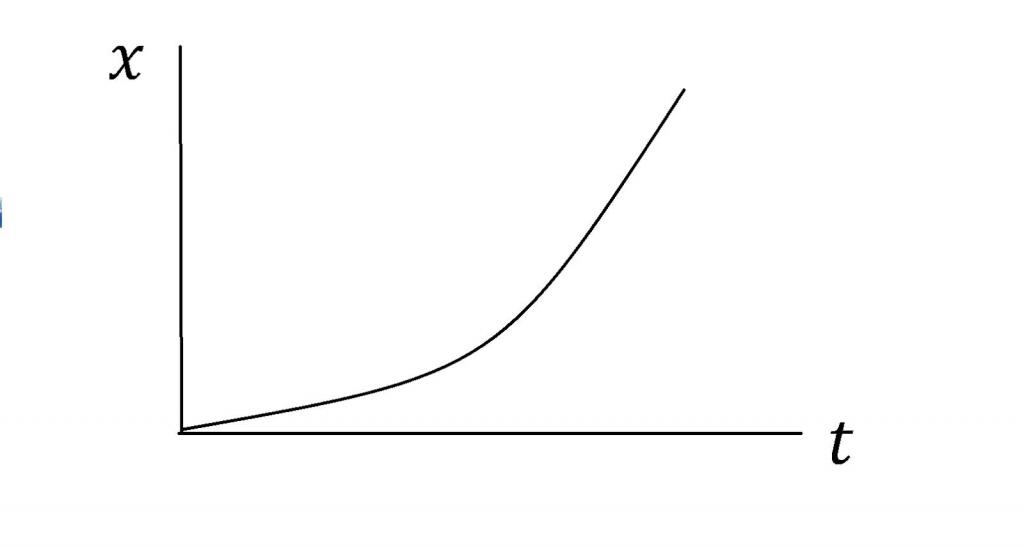
L = a * t 2/2;
L = v 0 * t + a * t 2/2;
L = v 0 * t - a * t 2/2
La prima espressione definisce il percorso per il movimento puro con accelerazione costante, la seconda equazione descrive il movimento accelerato con una velocità iniziale diversa da zero, la terza formula viene utilizzata per calcolare il percorso di frenata con altrettanto lento movimento.
Ad
Il compito di sollevare il corpo in un campo gravitazionale
Come notato sopra, la caduta libera si verifica con un'accelerazione costante. Il movimento con accelerazione è caratterizzato da una costante g, che vicino alla superficie del nostro pianeta è pari a 9,81 m / s 2 .
È noto che il corpo è stato gettato verticalmente. La velocità iniziale è di 30 m / s. È necessario calcolare l'altezza a cui il corpo si alza.
Questo compito è un tipico problema per lo spostamento uniforme in linea retta. Denotare l'altezza del rialzo con la lettera h. Sarà uguale al percorso che il corpo volerà fino al suo completo stop in altezza. Questa altezza è uguale a:
h = v 0 * t - g * t 2/2
Il tempo di volo può essere determinato dalla condizione di uguaglianza del valore di v a zero nel punto di massima altezza, cioè:
v = v 0 - g * t = 0 =>
t = v 0 / g
Sostituendo l'uguaglianza per t nella formula per h, otteniamo:
h = v 0 2 / g - g * (v 0 / g) 2/2 = v 0 2 / (2 * g)
Sostituendo il valore della velocità iniziale, arriviamo alla risposta: h = 45,9 metri.