Moto traslativo: definizione, formule, teorema
La meccanica considera tutti i possibili movimenti di un punto materiale e un corpo solido. Tutti loro sono descritti in diverse sezioni. Ad esempio, la domanda su come si muoverà sarà prerogativa della cinematica. Descrive in dettaglio il movimento traslatorio, oltre che più complesso - rotazionale. Innanzitutto, è più facile. Perché senza questo è difficile passare ai seguenti argomenti.
Quali presupposti consente un meccanico?
In molti problemi è permesso introdurre un'approssimazione. Ciò è dovuto al fatto che non influenzerà il risultato, ma semplificherà il corso del ragionamento.
La prima approssimazione è correlata alla dimensione del corpo. Se il corpo in esame è significativamente più piccolo degli altri nello stesso schema di riferimento, allora le sue dimensioni vengono trascurate. E il corpo stesso diventa un punto materiale.
Ad
Il secondo segue dall'assenza di deformazione nel corpo durante il suo movimento. O anche così insignificanti le sue dimensioni, che possono essere completamente trascurate.

Qual è il movimento di traslazione del corpo?
Per chiarimenti, dovrai considerare due punti qualsiasi all'interno del solido. Hanno bisogno di collegare il segmento. Se questo segmento rimane parallelo alla posizione iniziale durante il movimento, allora si dice che questo è un movimento in avanti.
Se c'è una negligenza delle dimensioni del corpo ed è considerato punto materiale Questo segmento è assente e si muove lungo la linea stessa.
Esempi vividi di un tale movimento
La prima cosa da ricordare è la macchina dell'ascensore. Illustra perfettamente il movimento in avanti del corpo. L'elevatore si muove sempre in modo rigido verso l'alto o verso il basso senza alcuna rotazione.
Ad
Il seguente esempio che illustra il movimento di traslazione è il movimento della cabina della ruota panoramica. Tuttavia, questo è vero solo in una situazione in cui la leggera pendenza della cabina all'inizio di ogni offset non viene presa in considerazione.
La terza situazione, quando è possibile parlare del movimento in avanti, è collegata al movimento dei pedali della bicicletta. Il loro movimento è considerato relativo al telaio. Anche in questo caso, viene introdotto il presupposto che i piedi di una persona non oscillano durante la guida.
L'elenco può essere completato spostando i pistoni, che oscillano all'interno dei cilindri del motore a combustione interna.

Concetti principali
La cinematica del movimento traslazionale è che studia e descrive il movimento di solidi e punti materiali. Tuttavia, lei non considera le ragioni che costringono il corpo a questo. Per descrivere un movimento, saranno necessarie le coordinate per indicare la sua posizione nello spazio. Inoltre, è richiesta la conoscenza della velocità e in qualsiasi momento.
Innanzitutto, vale la pena ricordare la traiettoria. È la linea lungo la quale si muove il corpo.
Il primo è inserire la mossa. È un vettore, che è denotato dalla lettera latina r. Può connettere l'origine con la posizione di un punto materiale. In altri casi, questo vettore viene disegnato dal punto iniziale a quello finale della traiettoria. Le unità di spostamento sono metri.
Il secondo valore che merita attenzione è il modo. È uguale alla lunghezza della traiettoria lungo la quale si muove il corpo. Il percorso è indicato dalla lettera alfabeto latino S, che è anche misurato in metri.

Formule di base
Ora è il momento di accelerare. Lei è anche un vettore. Inoltre, caratterizza non solo la direzione del movimento del corpo, ma anche la velocità del suo movimento. Il vettore di velocità è sempre diretto lungo la linea tangente, che può essere disegnata in qualsiasi punto della traiettoria. È indicato dalla lettera V. Le unità di misura sono m / s.
La velocità ad ogni istante di movimento può essere definita come la derivata del movimento nel tempo. Se il problema riguarda moto uniforme, allora la seguente formula è valida:
Ad
- V = S: t, dove t è il tempo di movimento.
In una situazione in cui la direzione del movimento cambia, devi utilizzare la somma di tutti i movimenti.
Il prossimo valore è l'accelerazione. Di nuovo, la quantità di vettori, che è diretta verso la velocità con un grande valore. È definito come la prima derivata della velocità nel tempo. La designazione accettata - la lettera "a". La dimensione è indicata in m / s 2 .
Le formule per ciascun componente di accelerazione, dirette lungo gli assi, sono calcolate come il rapporto tra la variazione di velocità lungo questo asse e l'intervallo di tempo. Se si crea una registrazione matematica, si ottiene quanto segue:
- e x = ΔV x : Δt.
Per le proiezioni di accelerazione su altri assi, le formule sono simili.
Inoltre, quando si considera il movimento lungo una traiettoria con curve, è possibile scomporre il vettore di accelerazione in due termini:
- a = a t + a n , dove a t è l'accelerazione tangenziale diretta lungo una tangente di flessione, e n è normale, che indica il centro di curvatura.
Il movimento di traslazione di qualsiasi corpo solido è ridotto a descrivere il movimento di uno solo dei suoi punti. Le formule da utilizzare sono:
- S = S 0 + V 0 t + (a 2 ): 2.
- V = V 0 + a.
In questa formula, gli indici "zero" denotano i valori iniziali delle quantità.
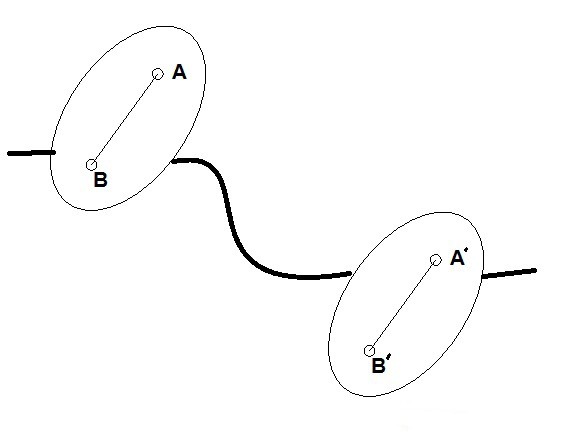
Teorema della magnitudo traslazionale
La sua formulazione è la seguente: la traiettoria, la velocità e l'accelerazione di tutti i punti del corpo sono le stesse durante il suo movimento in avanti.
Per dimostrarlo, è necessario scrivere la formula aggiunte vettoriali spostamento e vettore che collega due punti arbitrari. Le traiettorie di tutti i punti sono ottenute a causa del loro trasferimento lungo il secondo vettore. E non cambia la sua direzione e le dimensioni nel tempo. Pertanto, si può sostenere che tutti i punti del corpo si muovono lungo le stesse traiettorie.
Se prendiamo la derivata temporale, otteniamo il valore della velocità. Inoltre, l'espressione è semplificata nella misura in cui le velocità dei due punti sono uguali.
Il campo della derivata seconda è il risultato con l'uguaglianza delle accelerazioni dei due punti.