Angoli verticali: cos'è?

La geometria è una scienza antica e sorprendente. Punti, piani, linee rette, angoli, corpi solidi e figure piatte - questo è tutto ciò che questa disciplina accademica sta studiando. Teoremi, ipotesi e prove si basano su proprietà e leggi semplici e elementari. Gli angoli sono parte integrante della geometria. Sono nelle figure e nei corpi spaziali. E quali angoli sono chiamati verticali?

Angoli verticali: cos'è? definizione

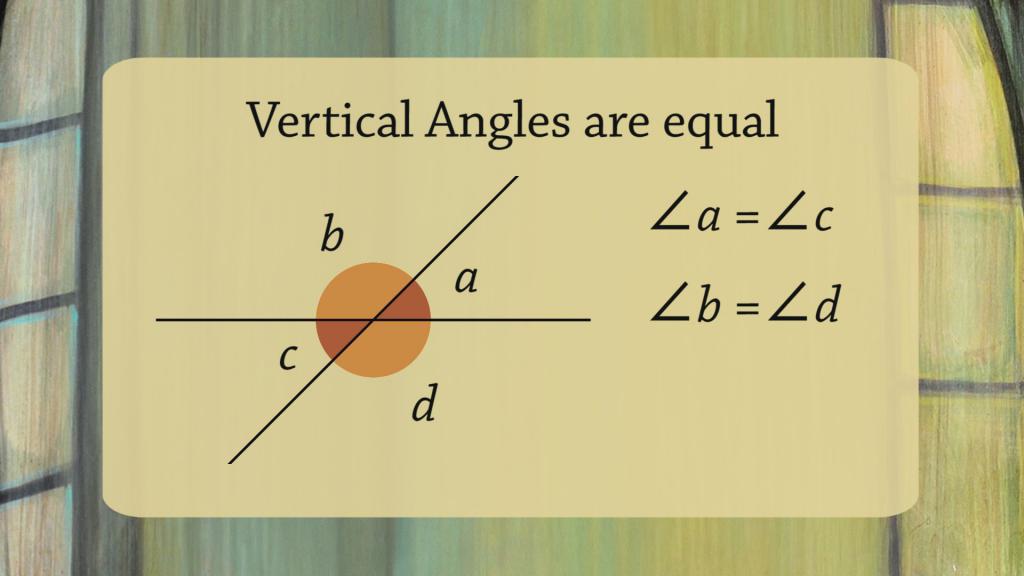
Gli angoli piatti, che sono ottenuti dall'intersezione di due linee rette, sono chiamati verticali - questa è la definizione di angoli verticali. Puoi considerarli sull'esempio di un triangolo. Se prendiamo qualsiasi angolo di questa figura, continuiamo le linee rette che lo fanno, otteniamo angoli verticali. Possono anche essere ottenuti imponendo su due linee rette parallele della linea di sezione. In questo caso, vengono formate quattro coppie di angoli verticali.

Teoremi e proprietà

• La proprietà principale e il teorema sugli angoli verticali è che sono uguali.
• Quando due linee rette si intersecano, risultano due coppie di verticali e quattro coppie di angoli adiacenti, la loro somma è di 360 gradi.
• Se viene fornita la misura in gradi di uno degli angoli verticali, è facile trovare il valore dei tre rimanenti. Uno degli angoli sarà uguale a questo. Gli altri due, che sono uguali tra loro, possono essere trovati sottraendo da 360 gradi la somma del noto e quindi il valore risultante diviso a metà.

Il teorema sugli angoli verticali è forse uno dei principali nella geometria, insieme ai "pantaloni pitagorici" e alla somma degli angoli di un triangolo. Tali angoli sono ovunque. Anche la lettera X è una specie di angolo verticale. La conoscenza dei teoremi e delle proprietà geometriche sottostanti aiuterà a gestire facilmente problemi più complessi e confusi. Devi solo includere la logica e l'immaginazione, e quindi il compito più complesso e complicato e le domande con gli asterischi sembreranno elementari.