Cos'è un cono in geometria? Definizione, formule, esempio di problema

La conoscenza delle proprietà delle figure geometriche consente non solo di risolvere problemi teorici, ma anche di eseguire calcoli praticamente importanti. Una di queste figure, le cui proprietà saranno discusse in questo articolo, è un cono. Cos'è un cono, di che tipo si tratta, come trovare la sua area e il suo volume? Tutte queste domande sono evidenziate in dettaglio di seguito.

Definizione generale di un cono in geometria

La stereometria, che studia le caratteristiche delle figure nello spazio tridimensionale, offre la seguente risposta alla domanda su cos'è un cono: si tratta di una figura la cui superficie è formata da un insieme di segmenti di linea retta che collegano un determinato punto nello spazio con una certa curva nel piano.

Il punto segnato dello spazio è chiamato vertice del cono, i segmenti retti sono i generatori della figura o dei suoi generatori e la curva stessa sul piano è la direttrice.

Secondo la definizione di cui sopra, è adatta un'intera classe di figure, le più famose delle quali sono coni rotondi, ellittiche, parabolici e iperbolici. La figura ellittica è mostrata sotto.

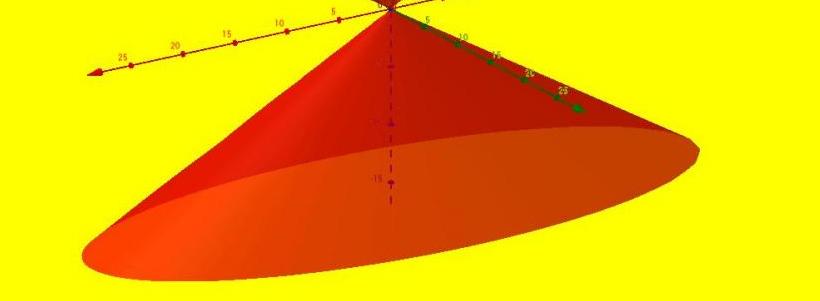
La direttrice di questo cono è un'ellisse chiusa che delimita la base della figura. Le generatrici di qualsiasi cono formano insieme una superficie conica, che viene chiamata laterale. Queste due superfici (la base e il lato) limitano il volume spaziale, che di solito è chiamato il volume del cono.

Cono dritto tondo - figura di rotazione

Il cono ellittico mostrato nella figura sopra non può essere ottenuto come risultato della rotazione di una figura piatta. L'unico rappresentante della classe di coni, che può essere formata per rotazione, è un cono rotondo tondo. Questa figura è mostrata sotto.

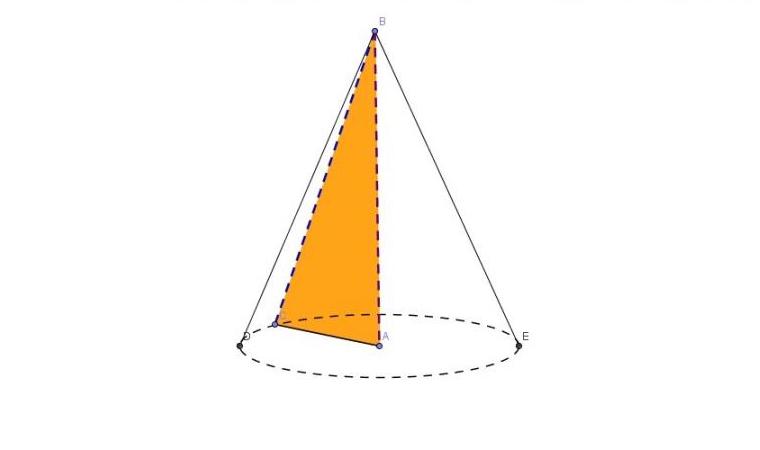
Si può vedere che la sua base rappresenta un cerchio ideale. Inoltre, qualsiasi sezione della superficie laterale con un piano parallelo alla base sarà anche un cerchio, ma con un diametro minore rispetto alla figura alla base.

Il triangolo arancione ABC, selezionato all'interno del cono, è rettangolare. Si può vedere che la sua gamba AC è il raggio di base r. La gamba AB è l'altezza della figura h. Per costruzione è chiaro che l'altezza è la lunghezza della perpendicolare disegnata dalla sommità della figura B al piano della base (cerchio). Questa altezza interseca il cerchio al centro. Quest'ultimo significa che il cono è dritto. Infine, l'ipotenusa del triangolo BC non è altro che una generatrice di coni.

Per formare un cono usando il triangolo descritto, è necessario ruotarlo attorno al lato AB.

Per una rappresentazione visiva della differenza tra coni dritti e obliqui, presentiamo la figura corrispondente.

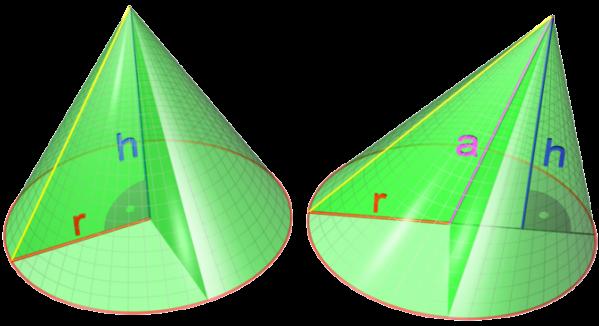
La differenza tra le due figure è evidente: se le loro basi sono le stesse, le altezze abbassate dalla cima incrociano le basi in punti diversi. La prima figura è diritta, la seconda è obliqua.

Parametri lineari di un cono rotondo tondo e angolo alla base

Questi parametri sono già stati indicati sopra. Elenca di nuovo:

• raggio r;
• altezza h;
• generatrice g.

Per definire un cono in modo univoco, questi tre parametri sono ridondanti, ovvero la figura in questione può essere costruita e tutte le sue proprietà possono essere calcolate, conoscendo solo due dei tre parametri denominati. Attingendo allo schema considerato per ottenere un cono ruotando un triangolo rettangolo, possiamo scrivere la seguente relazione tra generatore, raggio e altezza del cono:

g = √ (r² + h²).

Questa uguaglianza è ovvia e non richiede prove (ricorda il teorema di Pitagora).

È possibile impostare un cono non solo con l'aiuto di segmenti retti, h e g, ma anche utilizzando la misura angolare tra i generatori di forme e il piano di base. Indichiamo questo angolo con la lettera φ. Usando la definizione di funzioni trigonometriche, possiamo scrivere una serie di formule in cui l'angolo φ collega i parametri lineari. Scriviamo i principali:

g = h / sin (φ);

g = r / cos (φ);

h = r * tg (φ).

La superficie della figura

Considerando la domanda su cos'è un cono, presentiamo una formula per determinare l'area della sua intera superficie. Per rendere più chiaro ciò che verrà discusso, porteremo la scansione sul piano della figura in questione.

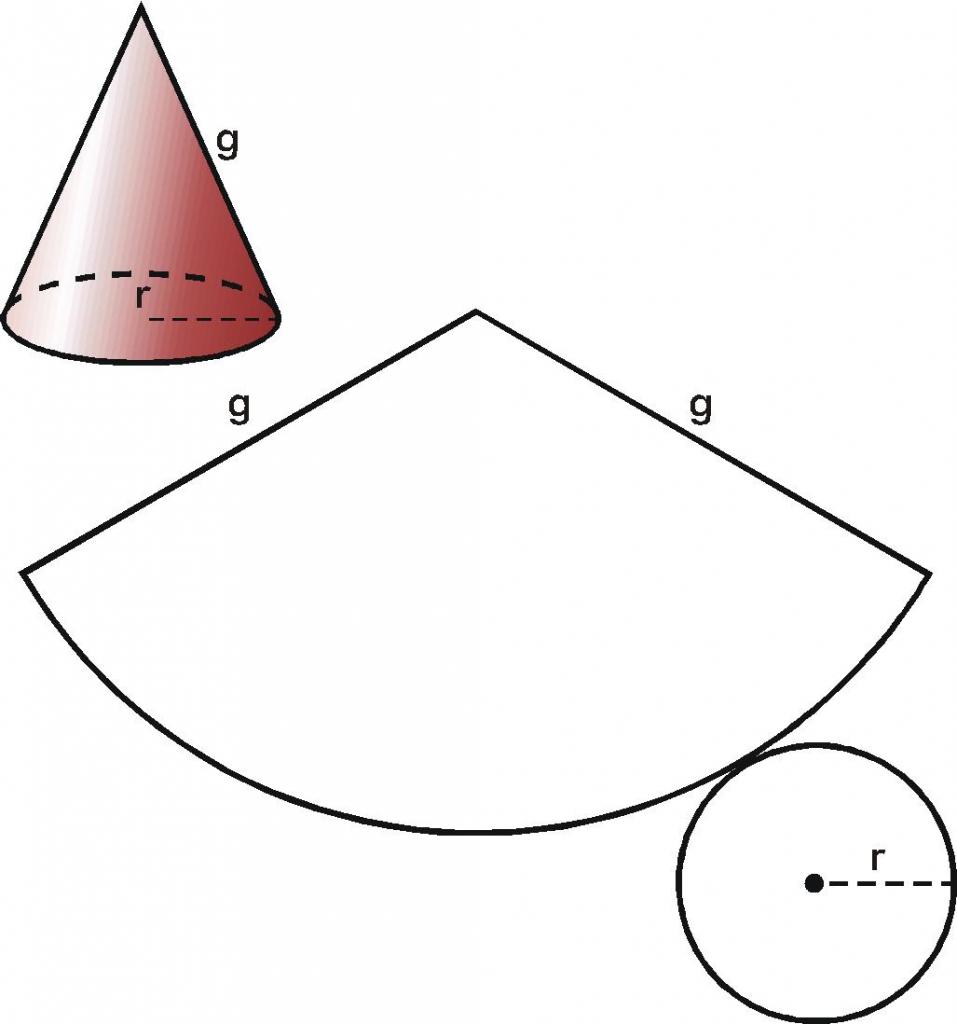
Lo sviluppo di un cono sul piano consiste di due figure. Il cerchio è la base del cono, il settore circolare del raggio g è la superficie laterale. Un settore circolare è facile da ottenere se si prende una superficie conica di carta e tagliata lungo qualsiasi generatrice g. Espandendo questa superficie, otteniamo il settore desiderato.

Determinare l'area S _{o il} cerchio non è un problema. L'espressione corrispondente è mostrata di seguito:

S _o = pi * r².

Per quanto riguarda il settore circolare, _sono noti anche i parametri necessari per il calcolo dell'area Sb: il raggio g e la lunghezza dell'arco corrispondente alla circonferenza del cerchio considerato sopra. La formula per calcolare l'area della superficie laterale del cono S _b è:

S _b = pi * r * g.

Pertanto, l'area totale della figura è uguale a:

S = S _o + S _b = pi * r * (r + g).

Formula per il volume

Sapendo cos'è un cono tondo, è facile scrivere la formula per il suo volume. Dato che la figura in questione può essere considerata una piramide con un numero infinito di bordi laterali, quindi per essa, come per qualsiasi piramide, il volume può essere calcolato con la formula:

V = 1/3 * S _o * h.

Il valore del quadrato S _o abbiamo già dato sopra, quindi, la formula richiesta per il volume di un cono dritto con una base rotonda sarà la seguente:

V = 1/3 * pi * r² * h.

Risolvere un problema geometrico

È noto che il valore della superficie di un cono di un rettilineo rotondo è di 300 cm². È necessario determinare il raggio del cono, sapendo che la sua generatrice è di 15 cm.

Scriviamo l'uguaglianza per l'area e sostituiamo il valore g = 15 cm e S = 300 cm², otteniamo:

S = pi * r * (r + g) =>

300 = pi * r² + 15 * pi * r.

Dividi i lati sinistro e destro per il numero pi, otteniamo la seguente equazione quadratica:

r² + 15 * r - 95.54 = 0.

Risolviamo questa equazione attraverso la discriminante, otteniamo:

D = 15² - 4 * (- 95,54) = 607,16;

r = (-15 ± √D) / 2 = (4,82; -19,82).

Una radice negativa non corrisponde alla condizione del problema, quindi puoi scrivere la risposta: il cono dato ha un raggio di 4,82 cm.