Cos'è un esagono regolare e quali attività possono essere associate ad esso?
La figura più famosa, che ha più di quattro angoli, è un esagono regolare. In geometria, è spesso usato nei problemi. E nella vita è esattamente questo tipo di nido d'ape sul taglio.
Com'è diverso dal torto?
Innanzitutto, l'esagono è una figura con 6 vertici. In secondo luogo, può essere convesso o concavo. Il primo si distingue per il fatto che i quattro vertici si trovano su un lato della retta tracciata attraverso gli altri due.
Terzo, un esagono regolare è caratterizzato dal fatto che tutti i suoi lati sono uguali. Inoltre, ogni angolo della figura ha lo stesso valore. Per determinare la somma di tutti i suoi angoli, è necessario utilizzare la formula: 180º * (n - 2). Qui n è il numero di vertici della forma, cioè, 6. Un semplice calcolo dà un valore di 720º. Cioè, ogni angolo è di 120 gradi.
Ad
Nelle attività quotidiane, l'esagono regolare si trova nel fiocco di neve e nel dado. I chimici lo vedono anche nella molecola del benzene.
Quali proprietà sono necessarie per sapere quando si risolvono i problemi?
Per quanto sopra, aggiungere:
- le figure diagonali disegnate attraverso il centro lo dividono in sei triangoli, che sono equilateri;
- il lato di un esagono regolare ha un valore che coincide con il raggio del cerchio descritto attorno ad esso;
- usando una tale forma, è possibile riempire il piano, e non ci saranno spazi tra loro e non ci saranno sovrapposizioni.
Designazioni introdotte
Tradizionalmente il lato giusto forma geometrica denotato dalla lettera latina "a". Per risolvere i problemi, sono necessari un'area e un perimetro aggiuntivi, rispettivamente S e P. Un cerchio è inscritto in un esagono regolare o descritto attorno ad esso. Quindi i valori vengono inseriti per i loro raggi. Sono indicati con le lettere r e R.
In alcune formule, appaiono l'angolo interno, il semiperimetro e l'apotema (che è perpendicolare al centro di entrambi i lati dal centro del poligono). Per loro, le lettere sono usate: α, p, m.
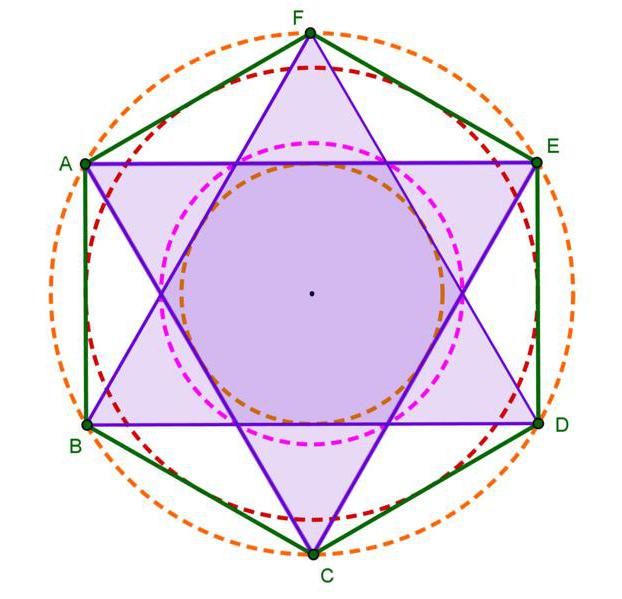
Formule che descrivono la forma
Per calcolare il raggio del cerchio inscritto, è necessario quanto segue: r = (a * √3) / 2, con r = m. Cioè, la stessa formula sarà per gli apothems.
Poiché il perimetro dell'esagono è la somma di tutti i lati, è definito come: P = 6 * a. Tenendo conto del fatto che il lato è uguale al raggio del circumcircle, per il perimetro esiste una formula per un esagono regolare: P = 6 * R. Da quello dato per il raggio del cerchio inscritto, viene derivata la relazione tra a e r. Quindi la formula assume la seguente forma: P = 4 r * √3.
Ad
Per l'area di un esagono regolare, può essere utile: S = p * r = (a 2 * 3 √3) / 2.
compiti
№ 1. Condizione. Esiste un prisma esagonale regolare, ogni lato del quale è uguale a 4 cm. Contiene un cilindro il cui volume è necessario conoscere.
La decisione Volume del cilindro è definito come il prodotto dell'area di base e dell'altezza. Quest'ultimo coincide con il bordo del prisma. Ed è uguale al lato di un esagono regolare. Cioè, l'altezza del cilindro è anche di 4 cm.
Per scoprire l'area della sua base, devi calcolare il raggio del cerchio inscritto nell'esagono. La formula per questo è data sopra. Pertanto, r = 2√3 (cm). Quindi l'area del cerchio: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (cm 2 ).
Resta da contare il volume: V = 37, 68 * 4 = 150,72 (cm 3 ).
La risposta è V = 150,72 cm 3 .
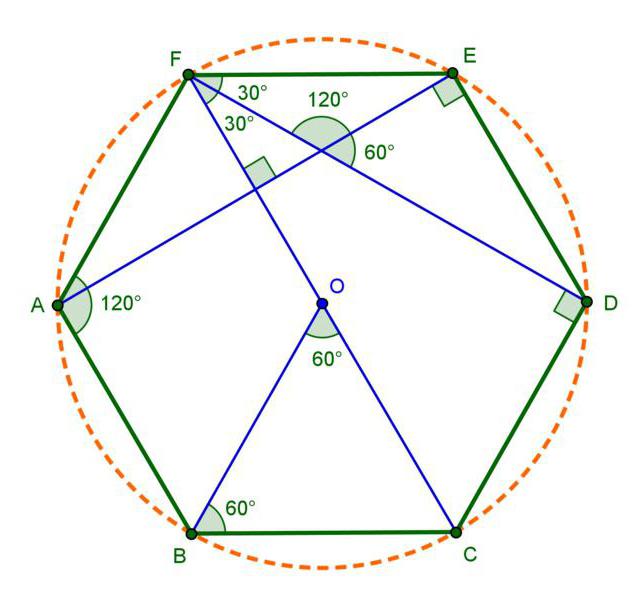
№ 2. Condizione. Calcola il raggio del cerchio, che è inscritto in un esagono regolare. È noto che il suo lato è di √3 cm. A cosa sarà uguale il suo perimetro?
La decisione Questo compito richiede l'utilizzo di due delle formule sopra. E devono essere applicati, anche senza modificare, basta sostituire il valore del lato e calcolare.
Quindi, il raggio del cerchio inscritto è di 1,5 cm. Per il perimetro, questo valore è vero: 6√3 cm.
La risposta è r = 1,5 cm, P = 6√3 cm.
№ 3. Condizione. Il raggio del circumcircle è di 6 cm. Qual è il valore del lato di un esagono regolare in questo caso?
La decisione Dalla formula per il raggio inscritto in un esagono di un cerchio, è facile ottenere quello con cui è necessario calcolare il lato. È chiaro che il raggio è moltiplicato per due e diviso per la radice di tre. È necessario liberarsi dell'irrazionalità nel denominatore. Pertanto, il risultato delle azioni assume la seguente forma: (12 √3) / (√3 * √3), cioè 4√3.
La risposta è a = 4√3 cm