Cos'è la geometria? Definizione, caratteristiche e specie

Cos'è la geometria? Questa è una scienza che studia le forme, le relazioni spaziali. La sezione di matematica dedicata alle figure e la loro disposizione reciproca ha una lunga storia. La scienza è comparsa nell'antichità. Il fondatore - il matematico Euclide.

Prima informazione

Cos'è la geometria? Questa è la scienza, che è considerata la culla dell'Egitto. All'inizio era una semplice imbarcazione di rilevamento terrestre. I greci trasformarono le informazioni ricevute dagli egiziani in una rigida disciplina. Nei tempi antichi, ciò che è la geometria è anche conosciuto in India, Cina, Assiria.

Nei tempi antichi, lo studio di questa scienza era causato dalla necessità di misurare la terra. Inoltre, i primi sviluppi significativi hanno richiesto livellamento, verticale sostenuta, assoluzione con un piano e una prospettiva. La necessità di misurare i tempi richiedeva l'osservazione sistematica del movimento dei luminari e, di conseguenza, la misurazione degli angoli. Cos'è la geometria? Questa è la scienza che ha permesso agli antichi di costruire enormi edifici. Alcuni di loro sono sopravvissuti fino ad oggi.

Talete di Mileto

La geometria è una scienza l'aspetto di cui gli autori greci associavano precisamente questo nome. L'attività di Talete di Mileto fu rappresentata dagli Elleni nella luce solare. È noto che nei giovani viaggiò in Egitto, comunicò con i sacerdoti egizi e imparò da loro sulla geometria. Questa scienza è molto interessata a Talete. Dopo essere tornato al villaggio, si stabilì a Mileto, dedicandosi al suo studio. Successivamente fondò la scuola ionica.

Cosa è importante sapere quando si lavora al progetto "Geometry around us"? Prima di tutto, sui motivi per cui questa scienza nei tempi antichi si sviluppò molto rapidamente. È importante conoscere, ovviamente, il significato della parola "geometria". Nonostante il fatto che le basi siano state poste dagli egiziani, il nome stesso della disciplina viene dal greco. Tradotto in russo, significa "misurare la terra".

In termini di architettura in rapida evoluzione, ingegneria civile, tecnologia civile e militare, il materiale scarso ottenuto dagli egiziani, i greci, ovviamente, non soddisfacevano. I metodi elementari di osservazione diretta erano impotenti di fronte a nuovi compiti.

La scuola ionica ha portato la scienza degli egiziani nella regione con una vasta gamma di idee e compiti. Ha dato il carattere teorico della geometria. La definizione presentata sopra cessò presto di corrispondere ai compiti originali.

Euclide

Approssimativamente IV c. fino al n. e. ha cominciato ad apparire primi lavori. Ad esempio, "Start". In questo lavoro, Euclide ha sistematizzato tutte le conoscenze acquisite in quel momento.

Ο Anche la vita di questo scienziato è quasi sconosciuta. Prima di noi c'erano solo alcune leggende su di lui. Il primo commentatore del programma "Inizio", che visse nel quinto secolo della nostra era, non poté nemmeno indicare dove Euclide nacque e morì.

Una delle leggende dice che il re Tolomeo una volta decise di studiare la geometria. Ma si è scoperto che non è così facile da fare. Quindi chiamò Euclide e gli chiese di dargli un modo facile. "Non esiste una strada regale per la geometria", ha detto lo scienziato. Quindi, sotto forma di leggenda, dacci un'espressione che è diventata alata.

Ad Alessandria, Euclide fondò una scuola matematica e scrisse un grande lavoro sulla geometria: "L'inizio". Si sostiene che sia stato scritto circa 325 anni prima della nostra era.

"Elementi"

Sia i modernisti che gli investigatori euclidei erano attratti dalle informazioni sistematiche e logiche. "The Beginnings" consiste di tredici libri, costruiti sotto un unico schema logico. Ognuno dei libri inizia identificando le tensioni (linea, linea, altezza, figura, ecc.) Che vengono utilizzate in esso, e quindi su un piccolo numero di esercizi di base (cinque axio e lo stesso non formato). geοmetrii.

Nell'Antichità, lo sviluppo della scienza non suggeriva l'esistenza di metodi di matematica pratica. I primi quattro libri coprivano la geometria, il loro contenuto era scritto dalle scuole pitagoriche. Nella quinta parte, è stata sviluppata la dottrina delle organizzazioni, che era adiacente a Eudox Ciddes. Nel quinto fino al nono libro c'era un insegnamento sui numeri, che rappresentava lo sviluppo delle fonti primarie pitagoriche. Le seguenti parti conterranno la distribuzione delle aree nello spazio e nello spazio (stereometria), la teoria dell'irrazionalità. Nel finale vengono poste le indagini sui corpi corretti.

Gli "inizi" di Euclide sono una rappresentazione di quella scienza, che è ancora conosciuta con il termine "geometria euclidea". Come ipotesi, l'autore ha scelto affermazioni che possono essere verificate con le asserzioni più semplici utilizzando una bussola e un righello. Euclide accettò anche alcune offerte generali - assiomi. Ad esempio, due quantità, uguali alla terza, sono uguali tra loro. Sulla base di tali costruzioni e dell'assioma, Euclide sviluppò rigorosamente e sistematicamente tutta la planimetria.

Archimedes

Lo scienziato possiede una formula per determinare l'area di un triangolo attraverso tre delle sue parti (erroneamente chiamata formula di Heron). L'antico matematico greco diede una teoria (non esaustiva) dei poligoni convessi corretti (corpi di Archimede). L'assioma di "Archimede" ha un significato speciale: dalla nitidezza disuguale, un numero minore sarà maggiore rispetto a distanze non uguali. Questo assioma determina il cosiddetto ordine archimedeo, che svolge un ruolo importante nella matematica moderna. L'antico matematico greco fece un numero che avrebbe registrato e dato un nome a numeri molto grandi. Con grande precisione, ha impostato il valore di un numero e indicato i limiti del peccato.

Cartesio

Il declino della società antica ha portato a una stasi comparativa nello sviluppo della geometria. Tuttavia, si è sviluppato in India, in Asia centrale, nei paesi dell'Est arabo. L'avvento delle scienze e delle arti in Europa ha attirato l'ulteriore fioritura della geometria. Nella scienza, un passo radicalmente nuovo fu fatto nella prima parte del XVII secolo da R. Descartes, che introdusse il metodo delle coordinate, che ci permette di associare la scienza all'algebra sviluppata e all'analisi emergente.

L'applicazione dei metodi di queste discipline ha dato origine ad altri tipi di geometria: analitica, e quindi differenziale. La scienza è passata a un livello qualitativamente nuovo. Ha già trattato cifre più generali e utilizza essenzialmente metodi nuovi.

tipi

La geometria analitica studia le figure e le trasformazioni date dalle equazioni algebriche nelle coordinate dirette, usando i metodi dell'algebra. Il differenziale, sorto nel XVIII secolo, esplora linee e superfici curve già abbastanza lisce, le loro famiglie e trasformazioni. Il suo nome è associato al metodo derivato dal calcolo differenziale.

XVII-XIX secolo

Per il primo quarto del XVII secolo fu iniziata l'origine della geometria proiettiva nelle opere di J. Dezargues e B. Pascal. È emerso dal problema dell'immagine dei corpi sul sito. Il suo primo oggetto è costituito da quelli delle opere d'arte, che vengono conservate quando sono progettate da un punto qualsiasi.

La forma primaria e la rappresentazione sistematica di queste nuove direzioni della geometria furono date all'inizio del 19 ° secolo da Eulero per l'analisi, per il differenziale, J. Fonsel per la geometria proiettiva. E l'insegnamento dell'immagine stessa (in diretto collegamento con i compiti del disegno) è stato sviluppato ancor prima e introdotto nel sistema da Monez sotto forma di geometria descrittiva. In tutte queste nuove discipline, i principi (assiomi, concetti originali) della scienza sono rimasti invariati. La gamma delle figure studiate e le loro proprietà, così come i metodi usati, si stava espandendo.

Lobachevsky

Nello sviluppo della scienza nel XIX secolo, inizia una nuova fase. C'era una geometria non euclidea (o Lobachevsky). Indipendente dal matematico russo nel 1832, lo stesso punto di vista fu formulato da J. Bolyai. Lobachevsky considerava la sua geometria come una potenziale teoria delle relazioni spaziali. Tuttavia, era ipotetico, sebbene il suo vero significato non fosse chiarito, e quindi la sua piena giustificazione fu data.

La rivoluzione della geometria, prodotta da Lobachevsky, nel suo valore non è inferiore a nessuna delle conversioni nella storia naturale. Non a caso è stato chiamato "Courier Geometry". Nelle sue idee sono stati delineati tre principi, che hanno determinato il nuovo sviluppo della disciplina.

Il primo è che non è solo la geometria euclidea che è logicamente concepibile, ma anche altri rami della scienza. Il secondo principio si basa sulla costruzione di nuove teorie modificando e sintetizzando i concetti di base formulati dall'antico matematico greco. Il terzo è, infatti, che la verità della teoria geometrica, nel senso della conformità con le proprietà reali dello spazio, può essere verificata solo dalla ricerca fisica, ed è possibile che in tal modo stabiliscano l'inesattezza della geologia euclidea. La fisica moderna lo ha confermato.

Inoltre, l'accuratezza matematica della geometria euclidea non viene persa. È determinato dalla logica (non continuità) della teoria dell'erudito greco antico. Allo stesso modo, in connessione con qualsiasi teoria geometrica, è necessario distinguere la loro verità fisica e matematica. Il primo è nel test di verifica in conformità con la validità. Nel secondo - in inconciliabilità logistica.

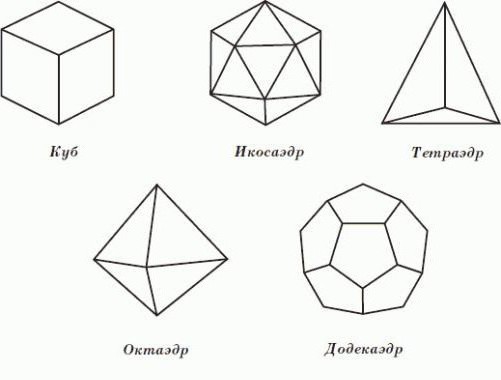
Qual è questa disciplina nel senso moderno del termine? La geometria è una scienza che comprende varie teorie matematiche. Sono storicamente sviluppati sulla base della geometria nel suo significato originale e nelle loro costruzioni sono derivati ​​dall'analisi, dalla sintesi e dalla modifica dei suoi cambiamenti. La geometria in questo senso generale è strettamente intrecciata con altri rami della matematica e i suoi confini non sono accurati.