Qual è l'integrale? Integrali con una soluzione dettagliata. Tavolo integrale
La parola "integrale" deriva dal latino integrale - olistico. Questo titolo è proposto nel 17 ° secolo. studente del grande Leibniz (e anche un matematico eccezionale) I. Bernoulli. E qual è l'integrale nel senso moderno? Di seguito cercheremo di dare una risposta esauriente a questa domanda.
Sfondo storico del concetto di integrale
All'inizio del 17 ° secolo nella considerazione dei maggiori scienziati c'era un gran numero di compiti fisici (principalmente meccanici) in cui era necessario indagare le dipendenze di alcune quantità sugli altri. I problemi più ovvi e urgenti erano la determinazione della velocità istantanea di un movimento irregolare del corpo in un dato momento e il suo problema inverso di trovare la grandezza del percorso percorso dal corpo per un certo periodo di tempo durante tale movimento. Oggi sappiamo già quale sia l'integrale della velocità di movimento - questo è il percorso che si è percorso. Ma capire come calcolarlo, conoscendo la velocità in ogni momento, non appare immediatamente.
All'inizio, dalla considerazione di tali dipendenze di grandezze fisiche, ad esempio, il percorso sulla velocità, si formò il concetto matematico della funzione y = f (x). Lo studio delle proprietà di varie funzioni ha portato all'emergere di analisi matematica. Gli scienziati stanno attivamente cercando modi per studiare le proprietà di varie funzioni. 
Come ha fatto il calcolo di integrali e derivati?
Dopo che Descartes ha creato le basi della geometria analitica e l'opportunità di rappresentare graficamente le dipendenze funzionali negli assi di un sistema di coordinate cartesiane, i ricercatori hanno affrontato due nuovi compiti principali: come disegnare una tangente a una linea curva in qualsiasi punto e come trovare l'area della figura delimitata sopra questa curva e linee rette, parallelo agli assi delle coordinate. In modo inaspettato, si è scoperto che il primo equivale a trovare la velocità istantanea e il secondo a trovare la distanza percorsa. Dopotutto, nel caso di movimenti irregolari, è stato rappresentato negli assi cartesiani di coordinate "distanza" e "tempo" con una certa linea curva.
Genius Leibniz e Newton nella metà del 17 ° secolo. sono stati creati metodi che hanno permesso di risolvere entrambi i problemi. Si è scoperto che per condurre una tangente ad una curva in un punto, è necessario trovare il valore della cosiddetta derivata della funzione che descrive questa curva nel suo punto in questione, e questo valore è uguale alla velocità di cambiamento della funzione, cioè con riferimento alla dipendenza da "percorso contro velocità" velocità istantanea del corpo.
Per trovare l'area delimitata da una curva, è stato necessario calcolare un certo integrale, che ha fornito il suo valore esatto. Derivata e integrale - i concetti di base del calcolo differenziale e integrale, che sono alla base della moderna analisi matematica - la sezione più importante della matematica superiore.
Area sotto la curva
Quindi, come definirlo valore esatto? Proviamo a rivelare il processo del suo calcolo attraverso l'integrale in dettaglio, fin dall'inizio.
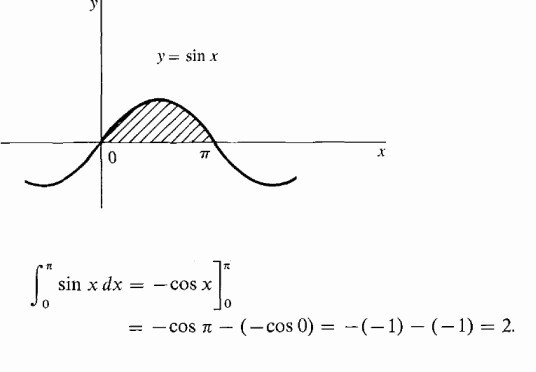
Sia f una funzione continua nell'intervallo [ab]. Considera la curva y = f (x) mostrata nella figura sottostante. Come trovare l'area dell'area delimitata dalla curva), l'asse xe le linee x = ae x = b? Cioè, l'area della figura ombreggiata nella figura. 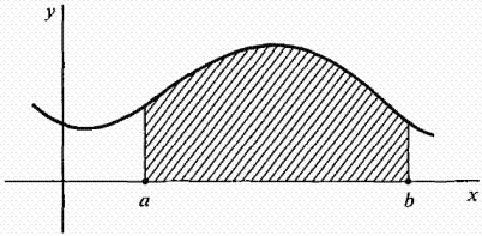
Il caso più semplice è quando f è una funzione costante; cioè, la curva è la linea orizzontale f (X) = k, dove k è una costante e k ≥ 0, come mostrato nella figura sottostante. 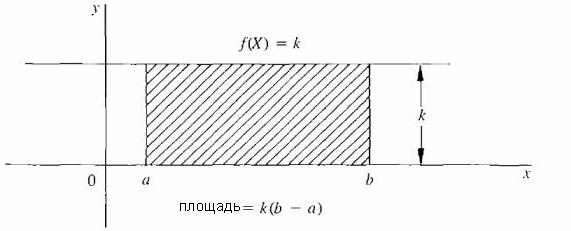 In questo caso, l'area sotto la curva è solo un rettangolo con altezza k e larghezza (b - a), quindi l'area è definita come: k · (b - a).
In questo caso, l'area sotto la curva è solo un rettangolo con altezza k e larghezza (b - a), quindi l'area è definita come: k · (b - a).
Le aree di alcune altre forme semplici, come il triangolo, il trapezio e il semicerchio, sono date da formule planimetriche.
L'area sotto qualsiasi curva continua y = f (x) è data da un integrale definito, che è scritto allo stesso modo di un integrale regolare.
Somma Riemann
Prima di immergerti in una risposta dettagliata alla domanda su cosa sia un integrale, evidenziamo alcune idee di base.
Innanzitutto, l'area sotto la curva è divisa in un certo numero n di strisce verticali di larghezza Δx sufficientemente piccola. Inoltre, ciascuna striscia verticale è sostituita da un rettangolo verticale di altezza f (x), larghezza Δx e area f (x) dx. Il prossimo passo è la formazione della somma delle aree di tutti questi rettangoli, chiamata somma di Riemannian (vedi le figure sotto).
Disegnando i nostri rettangoli Δx in larghezza, possiamo prendere la loro altezza uguale al valore della funzione sul bordo sinistro di ciascuna striscia, cioè la curva sarà i punti estremi a sinistra dei loro lati corti superiori Δx largo. Allo stesso tempo, nella sezione in cui la funzione cresce, e la sua curva è convessa, tutti i rettangoli sono al di sotto di questa curva, cioè la loro somma sarà certamente inferiore al valore esatto dell'area sotto la curva in quest'area (vedi figura sotto). Questo metodo di approssimazione è chiamato lato sinistro. 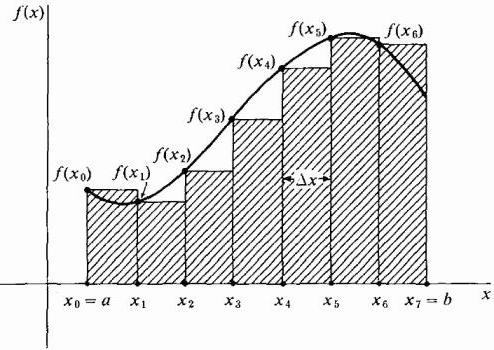
In linea di principio, è possibile disegnare rettangoli approssimati in modo tale che i punti estremi dei loro lati corti superiori di larghezza Δx giacciono sulla curva. Quindi saranno più alti della curva e l'approssimazione dell'area in quest'area sarà maggiore del suo valore esatto, come mostrato nella figura seguente. Questo metodo è chiamato il giusto. 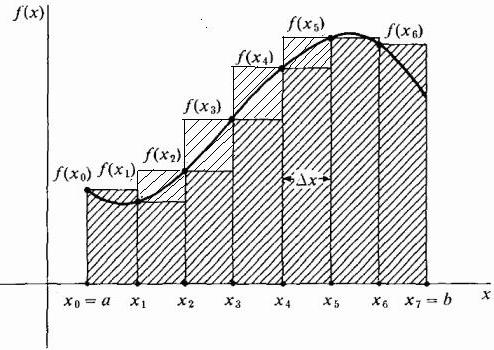
Ma possiamo anche prendere l'altezza di ciascuno dei rettangoli approssimativi uguale a un qualche valore della funzione in un punto arbitrario x * i all'interno della striscia corrispondente Δx i (vedi fig. qui di seguito). In questo caso, non possiamo nemmeno prendere la stessa larghezza di tutte le strisce. 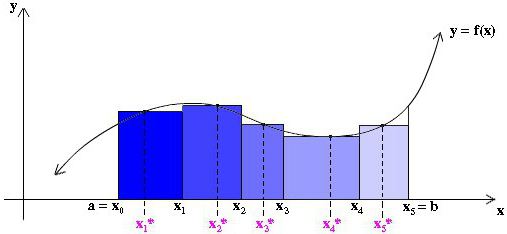
Facciamo l'importo di Riemann:

Transizione dalla somma di Riemann ad un integrale definito
Nella matematica superiore, viene dimostrato un teorema che afferma che se, con un aumento illimitato del numero n di rettangoli approssimativi, la loro larghezza massima tende a zero, allora la somma Riemanniana A n tende a qualche limite A. Il numero A è lo stesso per qualsiasi metodo di formazione di rettangoli e rettangoli per qualsiasi scelta di punti x * i .
Una chiara spiegazione del teorema è riportata nella figura seguente.
Mostra che, più ristretti i rettangoli, più l'area della figura a gradini si avvicina all'area sotto la curva. Quando il numero di rettangoli n → ∞, la loro larghezza è Δx i → 0, e il limite A della somma A n è numericamente uguale all'area richiesta. Questo limite e c'è un certo integrale della funzione f (x): 
Il simbolo integrale, che è una S modificata in corsivo, è stato introdotto da Leibniz. J. B. Fourier propose di mettere la notazione per l'integrale nella parte superiore e inferiore. Allo stesso tempo, i valori iniziali e finali di x sono chiaramente indicati.
Interpretazione geometrica e meccanica di un integrale definito
Proviamo a dare una risposta dettagliata alla domanda su che cos'è l'integrale? Considerare l'integrale nell'intervallo [a, b] della funzione positiva f (x) al suo interno e assumere che il limite superiore sia maggiore di quello inferiore Se le ordinate della funzione f (x) sono negative all'interno di [a, b], allora il valore assoluto dell'integrale è uguale all'area tra l'asse xe il grafico y = f (x), l'integrale stesso è negativo. Nel caso di un'intersezione singola o ripetuta dell'asse y = f (x) dell'ascissa sul segmento [a, b], come mostrato nella figura seguente, per calcolare l'integrale, è necessario determinare la differenza in cui la diminuzione è uguale all'area totale delle sezioni situate sopra l'asse x e deducibile - l'area totale delle aree sottostanti. L'interpretazione meccanica di un integrale definito è strettamente correlata al geometrico. Torniamo alla sezione "Riemann sum" e immaginiamo che il grafico mostrato nelle figure esprima la funzione della velocità v = f (t) con un movimento non uniforme punto materiale (l'asse delle ascisse è l'asse del tempo). Quindi l'area di un rettangolo di larghezza approssimativa Δt, che abbiamo costruito durante la formazione della somma di Riemann, esprimerà approssimativamente il percorso del punto durante il tempo Δt, vale a dire v (t *) Δt. La somma totale delle aree dei rettangoli nell'intervallo da t 1 = a to t 2 = b esprime approssimativamente il percorso s durante il tempo t 2 - t 1 , e il suo limite, cioè, l'integrale (definito) da a a b della funzione v = f (t) su dt fornirà il valore esatto del percorso s. Se torniamo alla sua designazione, allora possiamo ben presumere che a = const, e b sia il valore specifico di qualche variabile indipendente x. Quindi un integrale definito con un limite superiore x da un numero concreto si trasforma in una funzione di x. Tale integrale è uguale all'area della figura sotto la curva indicata dai punti aABb nella figura sottostante. Supponiamo di aver dato alla variabile x = b un piccolo incremento Δx. Quindi l'incremento dell'area della figura aABb è costituito dall'area del rettangolo (ombreggiata nella figura) Bb ∙ Δx e dall'area della figura BDC sotto la curva. L'area di un rettangolo è uguale a Bb ∙ Δx f = f (x) Δx, ovvero, è una funzione lineare dell'incremento della variabile indipendente. L'area della forma BDC è ovviamente più piccola dell'area del rettangolo BDCK = Δx ∙ Δy, e poiché Δx → 0 tende, diminuisce anche più velocemente di essa. Quindi, f (x) Δx = f (x) dx è il differenziale dell'area variabile aABb, cioè il differenziale di un integrale definito Da ciò possiamo concludere che il calcolo degli integrali consiste nel trovare le funzioni dalle espressioni date dei loro differenziali. Il calcolo integrale è precisamente il sistema di metodi per trovare tali funzioni dai loro differenziali noti. Connette la relazione tra differenziazione e integrazione e mostra che esiste un'operazione inversa alla differenziazione di una funzione - la sua integrazione. Mostra anche che se una qualsiasi funzione f (x) è continua, applicando questa operazione matematica ad essa è possibile trovare un intero insieme (set, set) di funzioni primitive per esso (o altrimenti, trovare un integrale indefinito da esso). Lascia che la funzione F (x) sia la designazione del risultato dell'integrazione della funzione f (x). La corrispondenza tra queste due funzioni come risultato dell'integrazione del secondo è indicata come segue: Come si può vedere, con il simbolo integrale non ci sono limiti all'integrazione. Ciò significa che da un definito si trasforma in un integrale indefinito. La parola "indefinito" significa che il risultato dell'operazione di integrazione in questo caso non è uno, ma molte funzioni. Infatti, oltre alla funzione F (x) stessa, qualsiasi funzione F (x) + C soddisfa le ultime espressioni, dove C = const. Ciò implica che il membro permanente nell'assemblea degli antiderivati può essere impostato arbitrariamente. Va sottolineato che se l'integrale definito dalla funzione è un numero, allora l'indefinito è una funzione, più precisamente, il loro insieme. Il termine "integrazione" è usato per definire la ricerca di entrambi i tipi di integrali. È l'esatto opposto della regola corrispondente per la differenziazione. Come vengono presi gli integrali indefiniti? Esempi di questa procedura, consideriamo le funzioni specifiche. Diamo un'occhiata alla funzione di potere della forma generale: f (x) = cx n Dopo aver fatto questo con ogni termine nell'espressione della funzione integrabile (se ce ne sono diversi), aggiungiamo una costante alla fine. Ricorda che prendere una derivata di valore costante la distrugge, quindi prendere l'integrale di qualsiasi funzione ci darà il ripristino di questa costante. Indichiamo con C, poiché la costante è sconosciuta - può essere qualsiasi numero! Pertanto, possiamo avere infinite espressioni per un integrale indefinito. Diamo un'occhiata a semplici integrali indefiniti, esempi dei quali sono mostrati sotto. Supponiamo di aver bisogno di trovare l'integrale della funzione: f (x) = 4x 2 + 2x - 3. Iniziamo con il primo termine. Guardiamo l'esponente 2 e lo aumentiamo di 1, quindi dividiamo il primo termine con l'indicatore risultante 3. Otteniamo: 4 (x 3 ) / 3. Quindi guardiamo il prossimo membro e facciamo lo stesso. Poiché ha l'esponente 1, l'indicatore risultante sarà 2. Quindi, dividiamo questo termine per 2: 2 (x 2 ) / 2 = x 2 . L'ultimo termine ha un fattore x, ma semplicemente non lo vediamo. Possiamo immaginare l'ultimo termine come (-3x 0 ). Questo è equivalente a (-3) ∙ (1). Se usiamo la regola di integrazione, aggiungiamo 1 all'indicatore per alzarlo al primo grado e poi dividiamo l'ultimo termine per 1. Otteniamo 3x. Questa regola di integrazione funziona per tutti i valori di n, eccetto n = - 1 (perché non possiamo dividere per 0). Abbiamo considerato l'esempio più semplice di trovare l'integrale. In generale, la soluzione degli integrali non è un compito facile, e l'esperienza già maturata in matematica è di grande aiuto. Nella sezione precedente, abbiamo visto che da ogni formula di differenziazione si ottiene una formula di integrazione corrispondente. Pertanto, tutte le loro possibili opzioni sono state a lungo ottenute e riassunte nelle tabelle corrispondenti. La seguente tabella di integrali contiene le formule per l'integrazione delle funzioni algebriche di base. Queste formule devono essere ricordate, memorizzandole gradualmente, dato che sono esercizi fissi. Un'altra tabella di integrali contiene le principali funzioni trigonometriche: Si scopre che, per fare questo, essere in grado di integrarsi, cioè trovare integrali indefiniti, è molto semplice. E la formula dei fondatori del calcolo integro-differenziale di Newton-Leibniz aiuta in questo. Secondo esso, nella prima fase, il calcolo dell'integrale desiderato consiste nel trovare l'indefinito, quindi calcolare il valore della primitiva trovata F (x) con la sostituzione di x, uguale prima al limite superiore, quindi a quello inferiore e infine, per determinare la differenza di questi valori. In questo caso, la costante C non può essere scritta. perché scompare quando si esegue la sottrazione. Consideriamo alcuni integrali con una soluzione dettagliata. Trova l'area del sito sotto un'onda sinusoidale a mezza onda. Consideriamo ora integrali con una soluzione dettagliata che utilizza la proprietà di additività nel primo esempio e la sostituzione della variabile di integrazione intermedia nel secondo esempio. Calcoliamo un integrale definito di una funzione razionalmente razionale: y = (1 + t) / t 3 da t = 1 a t = 2. Ora mostreremo come semplificare la presa dell'integrale introducendo una variabile intermedia. Supponiamo di aver bisogno di calcolare l'integrale di (x + 1) 2 . Abbiamo parlato di un integrale definito per un intervallo finito [a, b] di una funzione f (x) continua su di esso. Ma una serie di problemi specifici porta alla necessità di estendere il concetto di un integrale al caso quando i limiti (uno o entrambi) sono uguali all'infinito o quando una funzione discontinua. Ad esempio, quando si calcolano le aree sotto curve avvicinandosi asintoticamente agli assi delle coordinate. Per estendere il concetto di integrale a questo caso, oltre al passaggio al limite, quando si calcola la somma di Riemann dei rettangoli che si approssimano, viene eseguito un altro. Con un tale doppio passaggio al limite, si ottiene un integrale errato. Al contrario, tutti gli integrali menzionati sopra sono chiamati appropriati. 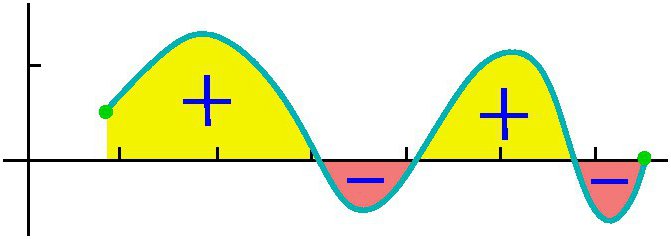 Pertanto, per la funzione mostrata nella figura sopra, l'integrale definito da a a b sarà (S1 + S3) - (S2 + S4).
Pertanto, per la funzione mostrata nella figura sopra, l'integrale definito da a a b sarà (S1 + S3) - (S2 + S4). Differenziale di un integrale definito
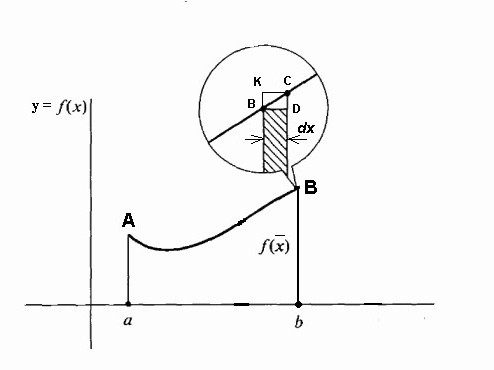 Con una linea fissa aA e una Bb in movimento, quest'area diventa una funzione di f (x), con gli incrementi Δx ancora depositati lungo l'asse x, e gli incrementi della funzione f (x) sono gli incrementi dell'area sotto la curva.
Con una linea fissa aA e una Bb in movimento, quest'area diventa una funzione di f (x), con gli incrementi Δx ancora depositati lungo l'asse x, e gli incrementi della funzione f (x) sono gli incrementi dell'area sotto la curva. 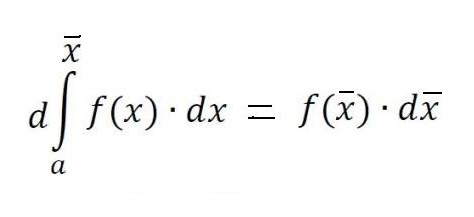
Il rapporto fondamentale del calcolo integrale
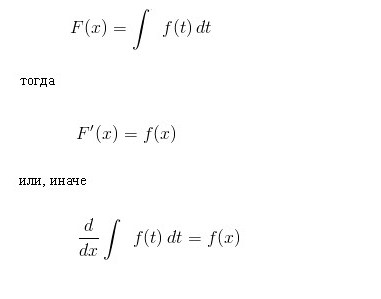
La regola di base dell'integrazione

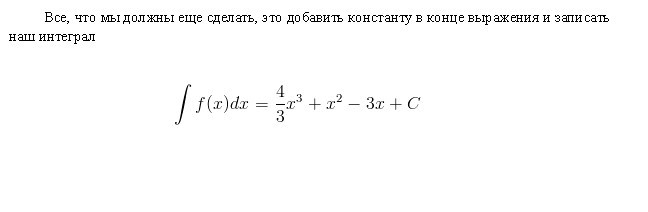

Tavoli integrali
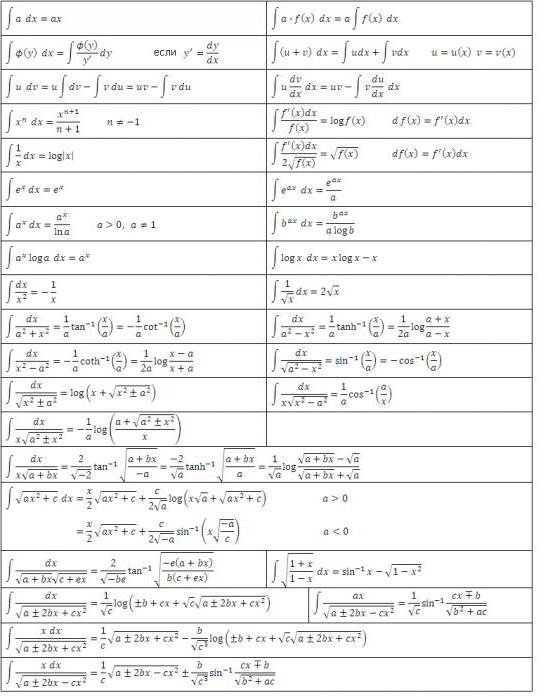

Come calcolare un certo integrale
 Calcola l'area ombreggiata sotto l'iperbole.
Calcola l'area ombreggiata sotto l'iperbole. 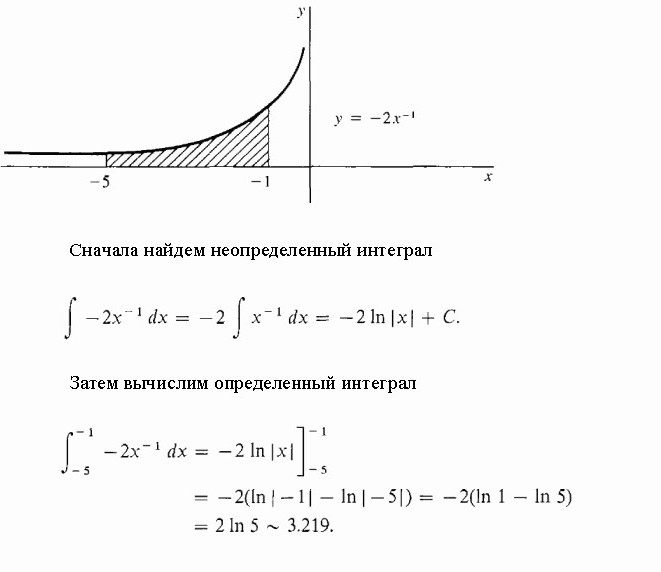
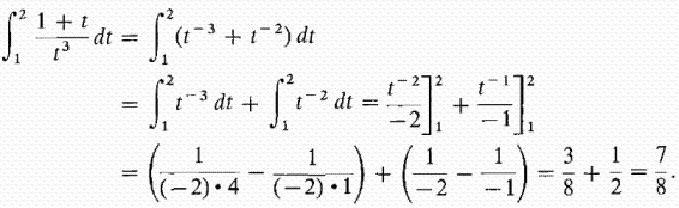
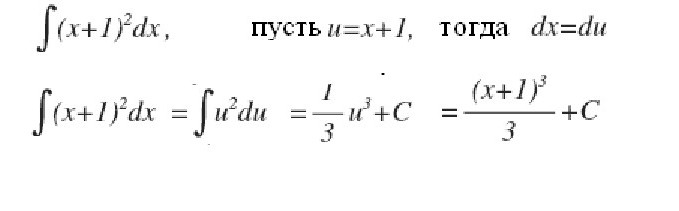
Informazioni sugli integrali impropri