Accelerazione della gravità: scoperta, cause, formula

L'accelerazione della caduta libera è una delle tante scoperte del grande Newton, che non solo riassume l'esperienza dei suoi predecessori, ma ha anche fornito una rigorosa spiegazione matematica di una grande quantità di fatti e dati sperimentali.

Prerequisiti della scoperta. Esperimenti galileiani

Uno dei tanti esperimenti di Galileo Galilei è stato dedicato allo studio del movimento dei corpi in volo. Prima di questo, nel sistema di visione del mondo prevaleva l'opinione che i corpi più leggeri cadessero più lentamente di quelli pesanti. Lancio di vari oggetti da un'altezza Torre pendente, Galileo ha scoperto che l'accelerazione della caduta libera per corpi con massa diversa è esattamente la stessa. Galileo ha giustamente attribuito le leggere discrepanze tra la teoria e i dati sperimentali all'influenza della resistenza aerea. Per dimostrare il suo ragionamento, propose di ripetere l'esperimento nel vuoto, ma a quel tempo non c'erano possibilità tecniche per questo. Solo molti anni dopo fece l'esperimento mentale di Galileo Isaac Newton.

Teoria di Newton

Onore della scoperta la legge del mondo appartiene a Newton, ma l'idea stessa è stata nell'aria per circa 200 anni. Il prerequisito principale per la formazione di nuovi principi della meccanica celeste divenne le leggi di Keplero, formulate da lui sulla base di molti anni di osservazione. Dall'oceano di supposizioni e congetture, Newton estrae un'ipotesi sulla forza di gravità del Sole e amplia la sua teoria al concetto di ampiezza del mondo. Ha testato la sua ipotesi sull'inverso proporzionalità della forza sul quadrato della distanza, avendo considerato l'orbita della luna. Successivi test di questa idea sono stati effettuati utilizzando lo studio del moto dei satelliti di Giove. I risultati delle osservazioni hanno mostrato che le stesse forze agiscono tra i satelliti dei pianeti e dei pianeti stessi, come nell'interazione tra il Sole e i pianeti.

Scoperta del componente gravitazionale

La forza di gravità della Terra verso il Sole obbedì alla formula:

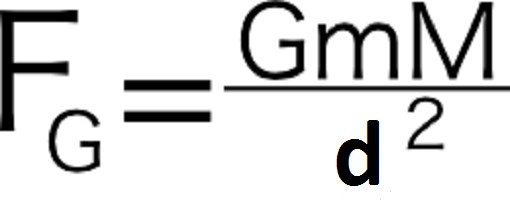
Gli esperimenti hanno dimostrato che il fattore 1 / d ² in questa relazione era abbastanza applicabile nel caso di considerazione di altri pianeti nel sistema solare. La costante G era il coefficiente che portava il valore della proporzione a un valore numerico.

Guidato dalla sua teoria, Newton misurava i rapporti di massa di vari corpi celesti, come la massa di Giove / la massa del Sole, la massa della Luna / la massa terrestre, ma Newton non poteva dare una risposta numerica alla domanda di quanto pesa la Terra, poiché la costante G rimase sconosciuta.

valore costante gravitazionale è stato scoperto solo mezzo secolo dopo la morte di Newton. Stime di questo valore basate su ipotesi, simili alle ipotesi di Newton, hanno dimostrato che questo valore è trascurabile ed è quasi impossibile calcolare il suo valore in condizioni terrestri. solito gravità Sembra enorme, perché tutti gli oggetti a noi familiari sono incredibilmente piccoli rispetto alla massa del globo.

La fine del XVIII secolo. Misurazione G

I primi tentativi di misurare G si sono verificati alla fine del XVIII secolo. Come forza trainante, hanno usato una grande montagna. La stima dell'accelerazione della caduta libera è stata effettuata sulla base della deviazione dalla verticale del peso del pendolo, che si trova nelle immediate vicinanze della montagna. Utilizzando i dati geologici, sono stati stimati la massa della montagna e la sua distanza media dal pendolo. Quindi abbiamo ottenuto la prima, piuttosto ruvida dimensione della misteriosa costante.

Lord Cavendish Dimensions

Lord Cavendish, nel suo laboratorio, eseguì le misurazioni dell'attrazione gravitazionale con il metodo della pesa libera. Per gli esperimenti, sono stati usati una palla di metallo e un enorme pezzo di metallo. Cavendish attaccò piccole palline di metallo ad una tavola sottile e portò loro grosse palle di piombo. Come risultato dell'impatto, la tavola si attorcigliò finché l'effetto dell'attrazione non compensò le forze di Hooke. L'esperimento era così sottile che persino il minimo soffio di vento poteva annullare i risultati della ricerca. Per evitare la convezione, Cavendish ha collocato tutti gli strumenti di misurazione in una grande scatola, quindi lo ha messo in una stanza chiusa e ha osservato l'esperimento con un telescopio.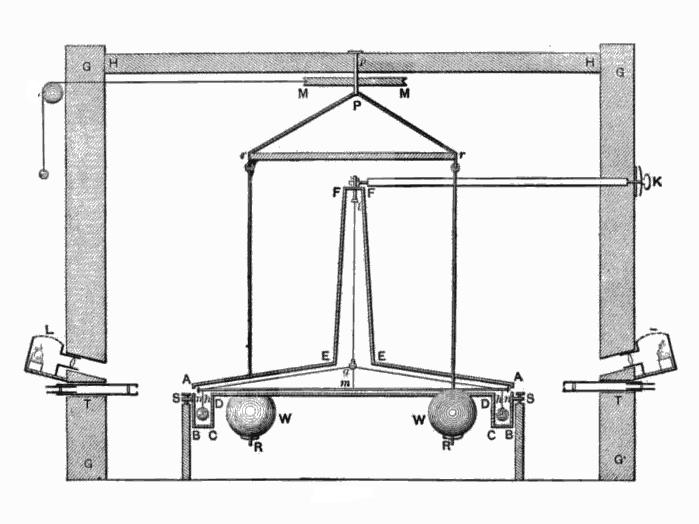

Calcolando la forza di torcere il filo, Cavendish stimò il valore di G, che fu successivamente solo leggermente aggiustato a causa di altri esperimenti più accurati. Nel moderno sistema di unità:

G = 6,67384 × 10 ^-11 m ³ kg ^-1 s ^-2 .

Questo valore è una delle poche costanti fisiche. Il suo valore è invariabile in qualsiasi punto dell'universo.

Misura dell'accelerazione terrestre

Secondo la terza legge di Newton, la forza di attrazione di due corpi dipende solo dalla loro massa e dalla distanza tra loro. Quindi, sostituendo nella parte destra dell'equazione un moltiplicatore noto dalla seconda legge di Newton, otteniamo:

ma = G (mM) / d ² .

Nel nostro caso, la massa m può essere ridotta e la quantità a è l'accelerazione con cui il corpo m viene attratto dalla Terra. Attualmente, l'accelerazione della gravità è solitamente indicata dalla lettera g. Otteniamo:

g = GM / d ² .

Nel nostro caso, d è il raggio della Terra, M è la sua massa, e G è la costante più elusiva che i fisici hanno cercato per molti anni. Sostituendo i dati noti nell'equazione, otteniamo: g = 9,8 m / s ² . Questo valore è l'accelerazione della caduta libera sulla Terra.

Valori G per diverse latitudini

Poiché il nostro pianeta non ha la forma di una palla, ma è un geoide, il suo raggio non è sempre lo stesso. La terra è appiattita, quindi l'accelerazione di caduta libera assumerà diversi valori all'equatore e ai due poli. In generale, la differenza nelle letture della lunghezza del raggio è di circa 43 km. Pertanto, in fisica, per risolvere i problemi, viene presa l'accelerazione dovuta alla gravità, che viene misurata ad una latitudine di circa 45 ⁰ . Molto spesso, per facilitare i calcoli, si presume che sia 10 m / s ² .

Valore G per la luna

Il nostro satellite obbedisce alle stesse leggi del resto dei pianeti nel sistema solare. A rigor di termini, quando si calcola l'accelerazione sulla superficie della luna, si dovrebbe anche tener conto dell'attrazione dal lato del sole. Ma, come si può vedere dalla formula, con l'aumentare della distanza, il valore della forza di attrazione diminuisce bruscamente. Pertanto, rifiutando tutte le forze secondarie, utilizzare la stessa formula:

G _L = GM / d ² .

Qui M è la massa della luna, e d è il suo diametro. Sostituendo i valori noti otteniamo il valore di G _L = 1,622 m / s ² . Questo valore è l'accelerazione della caduta libera sulla luna.

È un valore così basso di G _{L che} è la ragione principale dell'assenza di un'atmosfera sulla luna. Secondo alcune informazioni, all'alba dei tempi, il nostro satellite aveva un'atmosfera, ma a causa della debole attrazione, la Luna lo perse rapidamente. Tutti i pianeti con una grande massa di solito hanno la loro atmosfera. L'accelerazione della caduta libera è abbastanza grande per loro non solo per non perdere la propria atmosfera, ma anche per prendere del gas molecolare dallo spazio.

Riassumiamo alcuni risultati. L'accelerazione dovuta alla gravità è la quantità che ogni corpo materiale possiede. Non importa quanto sorprendente possa sembrare, ma tutto ciò che ha massa attira gli oggetti circostanti su se stesso. È solo che questa attrazione è così piccola che non importa nella vita di tutti i giorni. Tuttavia, gli scienziati sono seri anche sulle più piccole costanti fisiche, perché l'impatto che hanno sul mondo che ci circonda non è completamente compreso.