La legge di Ampere: formulazione e applicazione

La legge di Ampere, la cui formulazione è nota a qualsiasi fisico, è una delle quattro equazioni di Maxwell, che insieme costituiscono il fondamento dell'intera teoria dell'elettrodinamica classica.

Le equazioni di Maxwell

Parte della legge di Ampere su come le correnti elettriche, le fonti di campi magnetici, si riferiscono al campo stesso. In altre parole, questo (in congiunzione con la legge di Gauss per il magnetismo) descrive accuratamente l'immagine in cui le correnti elettriche generano campi magnetici. La parte correzionale di Maxwell è significativa perché dice che i campi magnetici appaiono quando i campi elettrici cambiano nel tempo. Questo è anche importante, poiché le equazioni di Maxwell non sono d'accordo senza di lui. Con la correzione del termine si possono ricavare formule salvate carica elettrica e prevedere l'esistenza di onde elettromagnetiche che viaggiano con velocità.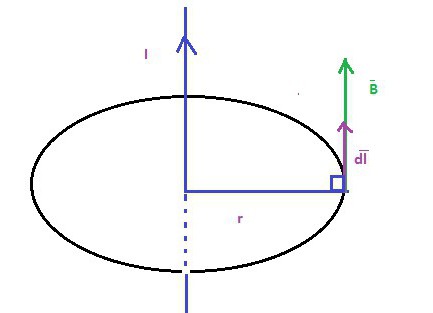

In una forma intelligibile, la legge di Ampere fa parte, rispettivamente, della linearità delle equazioni di Maxwell e, quindi, dell'intera teoria dell'elettrodinamica classica. Se si prendono due distributori di corrente e li si combinano, il campo magnetico sarà la somma dei campi magnetici prodotti da ciascuna configurazione.

Anche l'elemento di controllo di Maxwell è lineare e quindi onde elettromagnetiche sono anche lineari. Interferiscono tra loro secondo il principio di sovrapposizione e passano l'uno attraverso l'altro senza dispersione.

Come spiegare la legge di Ampere in un linguaggio semplice?

La spiegazione più semplice è che il filo trasporta corrente. Se ignori Campo magnetico terrestre si può immaginare che un filo verticale con una corrente elettrica sale.

Le persone tendono a parlare di elettromagnetismo, ma l'elettricità è separata dal magnetismo, perché è stato scoperto che l'elettricità e il magnetismo si influenzano a vicenda e possono essere combinati in un sistema di equazioni. In particolare, nel caso di conduttori vivi corrente elettrica produce un campo magnetico. L'orientamento di questi campi non è molto chiaro, ma è evidente. Le bussole magnetiche possono essere posizionate intorno a fili che trasportano corrente e le direzioni di campo possono essere viste nelle direzioni dei punti dell'ago.

È possibile considerarlo a causa della semplice simmetria. La corrente nel filo produce un campo magnetico, ma cosa dovrebbe accadere al modello in questi campi se il filo rimane verticale e ruota con una certa angolazione attorno a questo asse verticale? Il fatto è che la corrente non cambia in ogni caso in una tale svolta. Va ancora dritto. Pertanto, questa rotazione non può cambiare l'immagine del campo magnetico che viene prodotto.

struttura

Ci sono solo due possibili strutture che potrebbero funzionare da questo. O i campi sono diretti radialmente verso o lontano dal filo o attorno al filo. La prima possibilità è che le persone ottengano un campo elettrico da un filo elettricamente carico. La seconda possibilità è che puoi ottenere un campo magnetico creato dalla corrente attraverso i fili.

Per un campo a forma di singolo conduttore hanno strutture circolari al centro del filo e la forza del campo diminuisce con la distanza. Come schema, è molto simile alle increspature che si formano quando una pietra cade nell'acqua. Ci sono due principali differenze tra il laghetto e il modello del campo magnetico. Il primo è che il campo magnetico rimane invariato ad una certa distanza. Non crescerà, ma diminuirà in un dato punto. Il secondo è che il campo magnetico ha una direzione per ogni punto di tangenza del cerchio.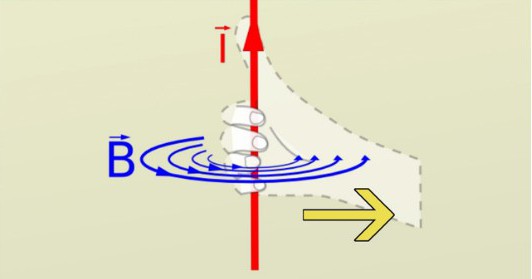

Corrente e distanza

La parte successiva della legge di Ampere afferma che la forza del campo magnetico dipende dalla forza della corrente e dalla distanza dal filo. Il risultato è che se si moltiplica il campo magnetico per la circonferenza del cerchio, questo prodotto sarà proporzionale alla forza della corrente elettrica. Cioè, se raddoppi la distanza dal filo, la linea della circonferenza si raddoppia e la magnitudine del campo magnetico diminuisce di 2 volte.

Ma la legge di Ampere ti consente di gestire le correnti prodotte in sistemi più complessi di un singolo filo. Ma tutti questi casi sono equivalenti. Questo significa che l'idea forza del campo magnetico moltiplicato per la lunghezza del percorso rimane utile e dipende ancora dalla somma di tutte le correnti all'interno del circuito che forma il percorso.

Come puoi capire la legge in senso pratico?

Ciò comporta un calcolo vettoriale che può essere spiegato in modo intuitivo:

• I campi magnetici sono creati da correnti elettriche.
• I campi magnetici sono "feriti" sulla corrente che li produce in una determinata direzione.
• Più è attuale, più forte è il campo magnetico creato. L'intensità del campo magnetico è proporzionale alla corrente.

La legge di Ampere lega questi concetti in una delle due formule matematiche. Il campo diventa più intenso man mano che si avvicina al filo.

Proporzionalità alla corrente totale

Nella forma integrale della legge di Ampere, viene utilizzato il concetto di integrale lineare. In linea di principio, puoi scegliere un ciclo specifico (cioè un percorso chiuso attraverso lo spazio) e camminare lungo un loop, sommare i componenti del campo magnetico. Questo mostrerà quanto il campo magnetico si avvolge attorno alla superficie delimitata dal loop. L'affermazione che questa quantità è proporzionale alla corrente totale, che è limitata dal ciclo, è vera.

Per capire questo, è necessario considerare il cavo di delimitazione del circuito. Se giri intorno a un filo, il campo magnetico si sposta sempre verso un punto nella stessa direzione, il che significa che la somma totale dell'integrale curvilineo sarà positiva. Dice che puoi andare in giro per la corrente! Inoltre, è possibile determinare la direzione della corrente usando la regola della mano destra. Se il flusso di corrente è andato in una direzione diversa, il valore dell'integrale curvilineo è invertito.

Ora possiamo supporre che sia stato preso un ciclo in cui uno non racchiude un filo, ma fa un cerchio in senso antiorario sul filo. Se cammini sul fondo del loop, nella maggior parte dei casi la direzione andrà a monte, quindi il contributo all'integrale sarà negativo. Ma quando la direzione passa attorno alla cima del loop, nella maggior parte dei casi sarà uguale alla corrente, quindi il contributo sarà positivo. Dice che non c'è nulla all'interno del ciclo (o non c'è affatto corrente, o correnti in direzioni opposte si compensano a vicenda).

differenziale

In forma differenziale, l'applicazione della legge di Ampere si verifica nel concetto di riccioli del dominio vettoriale. Un ricciolo è una dimensione quantitativa, un campo vettoriale è un "curling" attorno a un dato punto. Se prendiamo cicli sempre più piccoli intorno a un punto e calcoliamo l'integrale curvilineo, il risultato dovrebbe essere approssimativamente proporzionale all'area del ciclo. Il coefficiente di proporzionalità è arricciato.

Se si prende un ciclo che non contiene fili, l'integrale della linea sarà sempre zero. Se i loop sono più lontani e più lontani, sarà sempre zero. Il coefficiente di proporzionalità sarà uguale a zero e il rotore sarà uguale a zero (per essere esatti, il vettore zero). Ma se sei all'interno del cavo, non importa quale tipo di loop, riceverà la corrente che lo attraversa. L'idea è che per un circuito infinitamente piccolo, solo la densità di corrente in questo momento sarà "dentro" di esso, e solo la densità di corrente a questo punto determinerà il valore dell'integrale curvilineo. Pertanto, il rotore deve essere proporzionale alla densità di corrente in un dato punto, poiché è correlato al valore dell'integrale curvilineo su un loop infinitamente piccolo.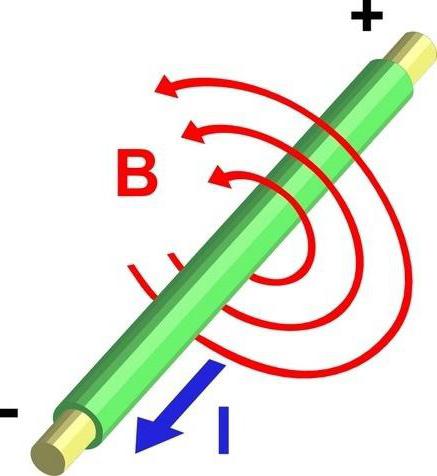

conclusione

Nelle forme differenziali e integrali, la legge di Ampere è equivalente, può essere mostrata applicando il teorema di Stokes. In sostanza, la forma differenziale è una versione infinitamente piccola della seconda equazione in "forma integrale". Ma il teorema di Stokes è un argomento per un altro studio.