Progressione aritmetica - sequenza numerica
Qualcuno diffida della parola "progressione" come termine molto complicato delle sezioni della matematica superiore. Nel frattempo, la più semplice progressione aritmetica è il lavoro di un banco dei taxi (dove rimangono ancora). E per capire l'essenza (e in matematica non c'è nulla di più importante di "capire l'essenza") di una sequenza aritmetica non è così difficile, avendo compreso diversi concetti elementari.
Sequenza numerica matematica
Una sequenza numerica viene solitamente chiamata una serie di numeri, ognuno dei quali ha il proprio numero.
e 1 - il primo membro della sequenza;
e 2 - il secondo membro della sequenza;
...
e 7 - il settimo membro della sequenza;
...
e n è l'n-esimo membro della sequenza;
Tuttavia, nessun insieme arbitrario di numeri e numeri ci interessa. La nostra attenzione sarà focalizzata su una sequenza numerica, in cui il valore dell'ennesimo termine è correlato al suo numero ordinale da una relazione che può essere chiaramente dichiarata matematicamente. In altre parole: il valore numerico dell'ennesimo numero è una funzione di n.
Ad
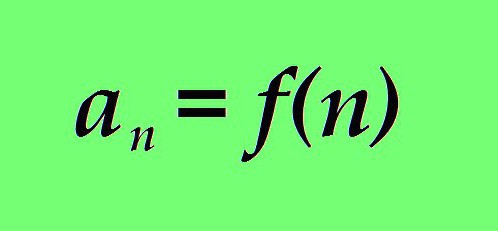
dove:
a è il valore di un membro di una sequenza numerica;
n è il suo numero di sequenza;
f (n) è una funzione, in cui il numero di sequenza nella sequenza numerica n è un argomento.
definizione
Una progressione aritmetica è chiamata sequenza numerica in cui ogni termine successivo è più (meno) del precedente per lo stesso numero. La formula per l'ennesimo termine di una sequenza aritmetica è la seguente:
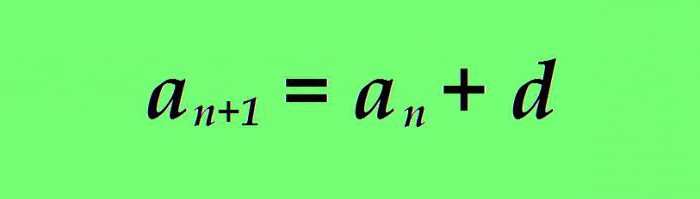
dove
a n - il valore del membro corrente della progressione aritmetica;
a n + 1 è la formula per il prossimo numero;
d - differenza (un certo numero).
È facile determinare che se la differenza è positiva (d> 0), allora ogni membro successivo della serie in esame sarà maggiore di quello precedente e tale progressione aritmetica aumenterà.
esempio:
a 1 = 5
d = 3
poi
numero di membro - n | 1 | 2 | 3 | 4 | 5 | 6 |
valore membro - un n | 5 | 8 | 11 | 14 | 17 | 20 |
Nel grafico sottostante, non è difficile tracciare perché la sequenza numerica sia chiamata "crescente".
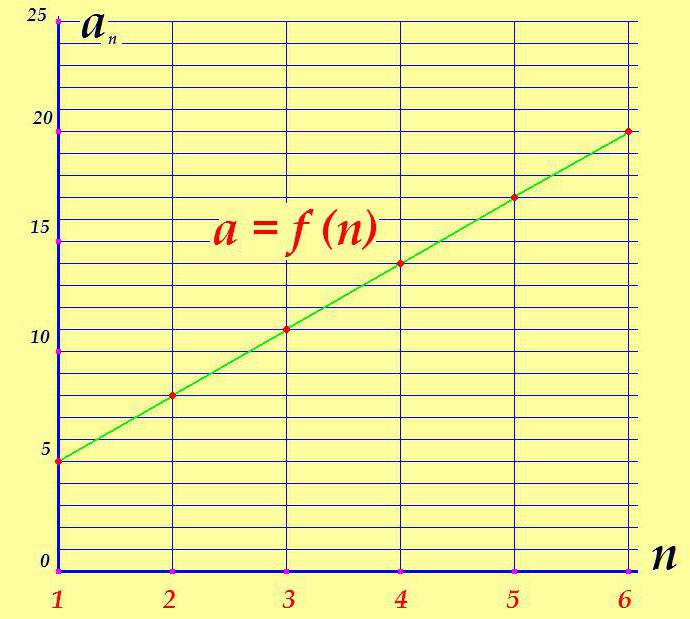
Nei casi in cui la differenza è negativa (d <0), ogni membro successivo, per ovvie ragioni, sarà inferiore a quello precedente, il grafico di progressione "andrà" in basso, la progressione aritmetica, rispettivamente, sarà indicata come una diminuzione.
Ad
Il valore del membro specificato
A volte è necessario determinare il valore di qualsiasi termine arbitrario a n di una progressione aritmetica. Puoi farlo calcolando in successione i valori di tutti i membri di una progressione aritmetica, dalla prima alla desiderata. Tuttavia, tale percorso non è sempre accettabile se, ad esempio, è necessario trovare il valore di un membro del cinquemilionesimo o dell'ottomillesimo. Il calcolo tradizionale richiederà molto tempo. Tuttavia, una determinata progressione aritmetica può essere studiata utilizzando determinate formule. C'è anche una formula per l'ennesimo termine: il valore di ogni membro di una progressione aritmetica può essere determinato come la somma del primo termine della progressione con la differenza della progressione moltiplicata per il numero del membro da trovare, ridotto di uno.
Ad
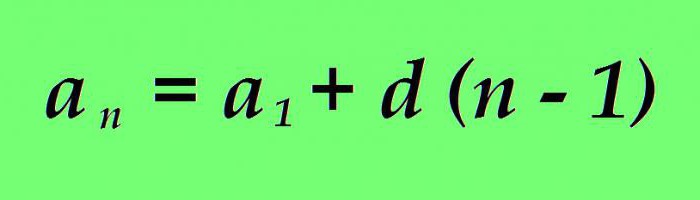
La formula è universale per la progressione ascendente e discendente.
Esempio di calcolo del valore di un determinato membro
Risolviamo il seguente problema di trovare il valore dell'ennesimo termine di una progressione aritmetica.
Condizione: c'è una progressione aritmetica con parametri:
- il primo termine della sequenza è 3;
- la differenza della serie di numeri è 1.2.
Compito: è necessario trovare il valore di 214 membri
Soluzione: per determinare il valore di un determinato membro, utilizziamo la formula:
a (n) = a1 + d (n-1)
Sostituendo nei dati di espressione dalle condizioni del problema abbiamo:
a (214) = a1 + d (n-1)
a (214) = 3 + 1,2 (214-1) = 258,6
Risposta: il 214 ° membro della sequenza è uguale a 258,6.
I vantaggi di questo metodo di calcolo sono evidenti: l'intera soluzione non richiede più di 2 righe.
La quantità di un dato numero di membri
Molto spesso, in una determinata serie aritmetica, è necessario determinare la somma dei valori di un certo segmento di esso. Per questo, non è inoltre necessario calcolare i valori di ciascun membro e quindi riepilogare. Questo metodo è applicabile se il numero di membri di cui si trova la somma è piccolo. In altri casi, è più conveniente utilizzare la seguente formula.
La somma dei membri di una progressione aritmetica da 1 an è uguale alla somma dei membri primo e n-th moltiplicata per il numero del membro n e divisa in due. Se nella formula il valore dell'n ° membro viene sostituito dall'espressione del paragrafo precedente dell'articolo, otteniamo:
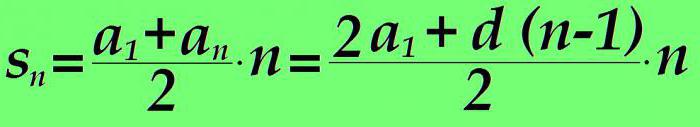
Esempio di calcolo
Ad esempio, risolvere il problema con le seguenti condizioni:
- il primo termine della sequenza è zero;
- la differenza è 0.5.
Il compito è determinare la somma dei membri della serie dal 56 al 101.
La decisione Usiamo la formula per determinare la quantità di progressione:
s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2
Innanzitutto, definiamo la somma dei valori di 101 membri della progressione, sostituendo nella formula i dati delle loro condizioni del nostro compito
s 101 = (2 ∙ 0 + 0.5 ∙ (101-1)) ∙ 101/2 = 2 525
Ovviamente, per scoprire la somma dei membri della progressione dal 56 al 101, è necessario sottrarre S 55 da S 101 .
s 55 = (2 ∙ 0 + 0.5 ∙ (55-1)) ∙ 55/2 = 742.5
Quindi la somma della progressione aritmetica per questo esempio:
s 101 - s 55 = 2 525 - 742,5 = 1 782,5
Un esempio dell'applicazione pratica della progressione aritmetica
Alla fine dell'articolo torneremo all'esempio della sequenza aritmetica fornita nel primo paragrafo: il tassametro (contatore di auto taxi). Considera questo esempio.
Ad
Atterrare in un taxi (che include 3 chilometri) costa 50 rubli. Ogni chilometro successivo viene pagato al ritmo di 22 rubli / km. La distanza di viaggio è di 30 km. Calcola il costo del viaggio.
1. Scartare i primi 3 km, il cui prezzo è incluso nel costo di atterraggio.
30 - 3 = 27 km.
2. Il calcolo ulteriore non è altro che un'analisi di una serie di numeri aritmetici.
Il numero membro è il numero di chilometri percorsi (meno i primi tre).
Il valore del membro è una somma.
Il primo termine in questo problema sarà uguale a 1 = 50 p.
La differenza di progressione d = 22 p.
il numero di interesse è il valore del (27 + 1) -esimo membro della progressione aritmetica - le letture del contatore alla fine del 27 ° chilometro - 27.999 ... = 28 km.
a 28 = 50 + 22 ∙ (28 - 1) = 644
Le formule che descrivono certe sequenze numeriche vengono utilizzate per calcolare i dati del calendario per un periodo arbitrariamente lungo. In astronomia, la lunghezza dell'orbita è in dipendenza geometrica dalla distanza di un corpo celeste verso una stella. Inoltre, varie serie numeriche sono applicate con successo nelle statistiche e in altri rami applicativi della matematica.
Ad
Un altro tipo di sequenza numerica è geometrico.
La progressione geometrica è caratterizzata da una grande, confrontata con la velocità aritmetica, del cambiamento. Non è un caso che in politica, sociologia e medicina si dica spesso che il processo si sviluppi in modo esponenziale per mostrare l'alto tasso di propagazione di un fenomeno, ad esempio, la malattia in un'epidemia.
Il termine Nth di una serie di numeri geometrici differisce dal precedente in quanto è moltiplicato per un numero fisso - il denominatore, ad esempio, il primo termine è 1, il denominatore è 2, rispettivamente:
n = 1: 1 ∙ 2 = 2
n = 2: 2 ∙ 2 = 4
n = 3: 4 ∙ 2 = 8
n = 4: 8 ∙ 2 = 16
n = 5: 16 ∙ 2 = 32,
n = 6: 32 ∙ 2 = 64 e così via ...
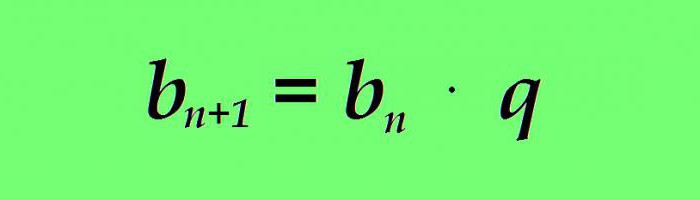
dove:
b n - il valore del termine corrente della progressione geometrica;
b n + 1 - la formula per il prossimo termine di una progressione geometrica;
q è il denominatore della progressione geometrica (numero costante).
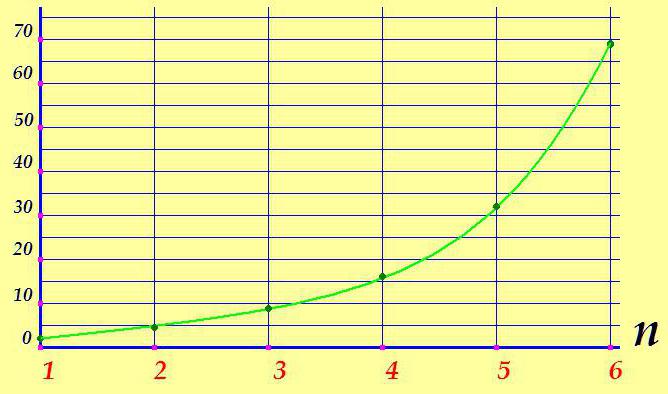
Se il grafico di una progressione aritmetica è una linea retta, quella geometrica disegna un'immagine leggermente diversa:
Come nel caso dell'aritmetica, la progressione geometrica ha la formula per il valore di un termine arbitrario. Qualsiasi termine n-esimo di una progressione geometrica è uguale al prodotto del primo termine dal denominatore della progressione al grado n ridotto di uno:
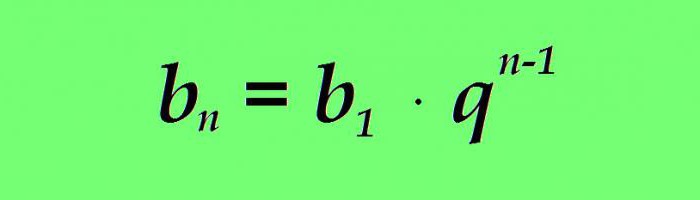
Un esempio Abbiamo una progressione geometrica con il primo termine uguale a 3 e il denominatore della progressione pari a 1,5. Trova il quinto membro della progressione
b 5 = b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875
Anche la somma di un determinato numero di membri viene calcolata utilizzando una formula speciale. La somma n dei primi termini di una progressione geometrica è uguale alla differenza tra il prodotto dell'ennesimo termine della progressione per il suo denominatore e il primo termine della progressione diviso per il denominatore ridotto di uno:
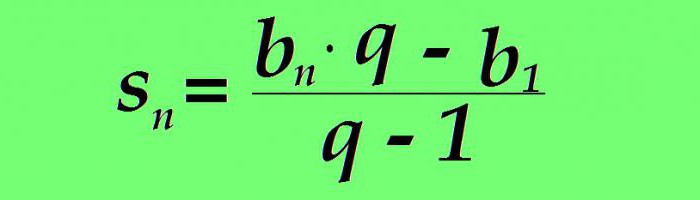
Se b n viene sostituito utilizzando la formula precedente, il valore della somma n dei primi membri della serie di numeri considerati assume la forma:
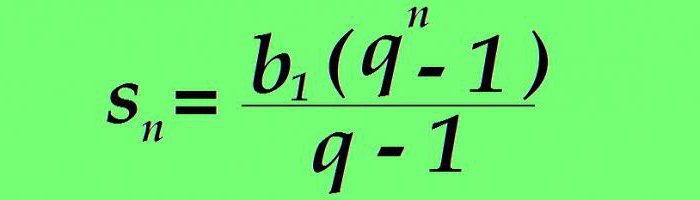
Un esempio Progressione geometrica inizia con il primo termine pari a 1. Il denominatore è impostato su 3. Trova la somma dei primi otto membri.
s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280