Concetti di base di teoria della probabilità e statistica matematica

La matematica include un'intera serie di aree, una delle quali, insieme all'algebra e alla geometria, è la teoria della probabilità. Ci sono termini comuni a tutte queste aree, ma, oltre a loro, ci sono specifiche, peculiari di una sola particolare "nicchia" di parole, formule, teoremi.

La frase "teoria della probabilità" provoca un panico in uno studente non preparato. In effetti, l'immaginazione dipinge immagini, dove appaiono formule volumetriche terribili e la soluzione di un problema occupa un intero quaderno. Tuttavia, in pratica, le cose non sono affatto così terribili: è sufficiente capire una volta il significato di alcuni termini e arrivare al nocciolo di una peculiare logica del ragionamento per non avere più paura dei compiti una volta per tutte. A questo proposito, consideriamo i concetti di base della teoria della probabilità e della statistica matematica: un campo di conoscenza giovane ma estremamente interessante.

Perché insegnare concetti

La funzione del linguaggio è quella di trasmettere informazioni da una persona all'altra in modo che lui la capisca, la comprenda e sia in grado di usarla. Ogni concetto matematico può essere spiegato con parole semplici, ma in questo caso l'atto dello scambio di dati richiederebbe molto più tempo. Immagina che invece della parola "ipotenusa" dovresti sempre dire "il lato più lungo di un triangolo rettangolo" - questo è estremamente scomodo e lungo.

Pertanto, le persone inventano nuovi termini per determinati fenomeni e processi. I concetti base della teoria della probabilità - l'evento, la probabilità di un evento, ecc. - sono apparsi allo stesso modo. Quindi, per usare le formule, risolvere i problemi e applicare le abilità nella vita, è necessario non solo memorizzare le nuove parole, ma anche capire cosa significa ognuno di loro. Più profondamente diventi consapevole di loro, approfondisci il significato, più ampia diventa la portata delle tue possibilità e più pienamente percepisci il mondo intorno a te.

Qual è il significato del soggetto

Facciamo conoscenza con i concetti di base della teoria della probabilità. La definizione classica di probabilità è la seguente: questo è il rapporto tra i risultati che si adattano al ricercatore al numero totale di possibili. Facciamo un semplice esempio: quando una persona tira un dado, può far cadere uno dei sei lati verso l'alto. Quindi, il numero totale di risultati è sei. La probabilità che un lato selezionato casualmente cada è 1/6.

La capacità di prevedere l'emergere di un particolare risultato è estremamente importante per vari specialisti. Quante parti difettose sono previste in molto? Dipende da quanto produrre. Qual è la probabilità che il farmaco aiuti a combattere la malattia? Questa informazione è vitale. Ma non perdiamo tempo con esempi aggiuntivi e continuiamo a studiare una nuova area per noi.

Prima conoscenza

Considera i concetti di base della teoria della probabilità e il loro uso. il giusto naturale le formule di scienze, economia e termini presentati di seguito vengono utilizzate ovunque, in quanto sono direttamente correlate alle statistiche e agli errori di misurazione. Uno studio più dettagliato di questa domanda ti aprirà nuove formule utili per calcoli più accurati e complessi, ma iniziamo con una semplice.

Uno dei concetti più basilari e fondamentali della teoria della probabilità e della statistica matematica è un evento casuale. Spiega con parole chiare: di tutti i possibili esiti di un esperimento, ne viene osservato solo uno. Anche se la probabilità di accadimento di questo evento è molto più alta dell'altro, sarà accidentale, poiché teoricamente il risultato potrebbe essere diverso.

Se abbiamo condotto una serie di esperimenti e ottenuto un certo numero di risultati, la probabilità di ognuno di essi è calcolata utilizzando la formula: P (A) = m / n. Ecco, m è quante volte nella serie di test abbiamo visto il risultato che ci interessa. A sua volta, n è il numero totale di esperimenti eseguiti. Se lanciavamo una moneta 10 volte e ottenevamo una "croce" 5 volte, allora m = 5 e n ​​= 10.

Tipi di eventi

Succede che alcuni risultati sono garantiti per essere osservati in ogni prova - un tale evento sarà chiamato affidabile. Se non succede mai, sarà chiamato impossibile. Tuttavia, tali eventi non sono usati nelle condizioni dei problemi sulla teoria della probabilità. I concetti base che sono molto più importanti da sapere sono eventi congiunti e incompatibili.

Accade che durante l'esperimento due eventi si verificano contemporaneamente. Per esempio, tiriamo due dadi - in questo caso, il fatto che uno abbia "sei" caduto non garantisce che il secondo non cada nel secondo. Tali eventi saranno chiamati congiunti.

Se tiriamo un dado, allora due numeri allo stesso tempo non potranno mai cadere. In questo caso, i risultati sotto forma di "uno", "due", ecc. Saranno considerati come eventi incompatibili. È molto importante distinguere quali esiti hanno luogo in ciascun caso specifico - dipende da quali formule utilizzare nel problema di trovare le probabilità. I concetti di base della teoria della probabilità, continueremo a studiare alcuni paragrafi dopo, quando considereremo le caratteristiche di addizione e moltiplicazione. In effetti, senza di loro, nessun problema può essere risolto.

Quantità e prodotto

Supponiamo che tiri un dado con un amico e che abbia un "quattro". Hai bisogno di ottenere cinque o sei per vincere. In questo caso, le probabilità saranno riassunte: poiché le probabilità di far cadere entrambi i numeri sono 1/6, la risposta sarà simile a 1/6 + 1/6 = 1/3.

Ora immagina di tirare un dado due volte e il tuo amico ha 11 punti. Ora è necessario avere "sei" due volte di seguito. Gli eventi sono indipendenti l'uno dall'altro, quindi la probabilità deve essere moltiplicata: 1/6 * 1/6 = 1/36.

Tra i concetti di base e i teoremi della teoria della probabilità dovrebbe prestare attenzione alla somma delle probabilità di eventi congiunti, t. cioè, quelli che possono accadere contemporaneamente. La formula di aggiunta in questo caso sarà simile a questa: P (A + B) = P (A) + P (B) - P (AB).

combinatorio

Molto spesso dobbiamo trovare tutte le combinazioni possibili di alcuni parametri di un oggetto o calcolare il numero di qualsiasi combinazione (ad esempio, quando si seleziona un codice). Combinatorics, che è strettamente connesso con la teoria della probabilità, ci aiuterà in questo. I concetti di base qui includono alcune nuove parole, e un certo numero di formule da questo argomento sarà sicuramente utile.

Supponiamo di avere tre numeri: 1, 2, 3. È necessario, usandoli, scrivere tutti i possibili numeri a tre cifre. Quanti ci saranno? Risposta: n! (punto esclamativo significa fattoriale). Le combinazioni di un numero di elementi diversi (numeri, lettere, ecc.), Che differiscono solo nell'ordine della loro posizione, sono chiamate permutazioni.

Tuttavia, più spesso incontriamo una situazione del genere: ci sono 10 cifre (da zero a nove), di cui è composta la password o il codice. Supponiamo che la sua lunghezza sia di 4 caratteri. Come calcolare il numero totale di possibili codici? Per questo c'è una formula speciale: (n!) / (N - m)!

Data la condizione di problema proposta sopra, n = 10, m = 4. Inoltre, sono richiesti solo semplici calcoli matematici. A proposito, tali combinazioni saranno chiamate collocamento.

Infine, c'è il concetto di combinazioni: si tratta di sequenze che differiscono l'una dall'altra da almeno un elemento. Il loro numero è calcolato dalla formula: (n!) / (M! (Nm)!).

Aspettativa matematica

Un concetto importante che lo studente incontra già nelle prime classi sull'argomento è l'aspettativa matematica. È la somma di tutti i possibili valori dei risultati moltiplicati per le loro probabilità. In sostanza, questo è un numero medio che possiamo prevedere come risultato di un test. Ad esempio, ci sono tre valori per i quali le probabilità sono mostrate tra parentesi: 0 (0,2); 1 (0,5); 2 (0,3). Calcolare l'aspettativa: M (X) = 0 * 0,2 + 1 * 0,5 + 2 * 0,3 = 1,1. Quindi, dall'espressione proposta possiamo vedere che questo valore è costante e non dipende dall'esito del test.

Questo concetto è usato in molte formule e lo incontrerai ripetutamente in futuro. È facile lavorare con lui: l'aspettativa della somma è uguale alla somma del tappeto. aspettative - M (X + Y) = M (X) + M (Y). Lo stesso vale per il prodotto: M (XY) = M (X) * M (Y).

dispersione

Deve provenire da un corso di fisica della scuola che ricordi che la dispersione si sta disperdendo. Qual è il suo posto tra i concetti di base della teoria della probabilità?

Guarda due esempi. In un caso, ci viene dato: 10 (0,2); 20 (0,6); 30 (0,2). Nell'altro - 0 (0,2); 20 (0,6); 40 (0,2). L'aspettativa matematica in entrambi i casi sarà la stessa, quindi come possiamo confrontare queste situazioni? Dopo tutto, vediamo a occhio nudo che la diffusione dei valori nel secondo caso è molto più grande.

Per questo è stato introdotto il concetto di dispersione. Per ottenerlo, è necessario calcolare l'aspettativa della somma delle differenze di ogni variabile casuale e dell'aspettativa. Prendi i numeri dal primo esempio registrato nel paragrafo precedente.

Per prima cosa calcoliamo l'aspettativa: M (X) = 10 * 0.2 + 20 * 0.6 + 30 * 0.2 = 20. Quindi il valore della varianza: D (X) = 40.

Un altro dei concetti di base della statistica e della teoria della probabilità è la deviazione standard. Calcola è molto semplice: devi solo prendere radice quadrata dalla dispersione.

Qui possiamo notare un termine così semplice, come l'ambito. Questo valore indica la differenza tra i valori massimo e minimo nell'esempio.

statistica

Molto spesso vengono usati concetti scientifici di base nella scuola. Due di questi sono media aritmetica e mediana. Sicuramente ti ricordi come trovare i loro valori. Ma nel caso, ricordiamo: la media aritmetica è la somma di tutti i valori divisi per il loro numero. Se il valore è 10, aggiungiamo e dividiamo per 10.

La mediana è centrale per tutto il possibile. Se abbiamo un numero dispari di valori, li scriviamo in ordine crescente e scegliamo quello che era nel mezzo. Se abbiamo un numero pari di valori, prendiamo due centrali e dividiamo per due.

Altri due valori, posizionati tra la mediana e i due estremi - massimo e minimo - dei valori dell'insieme, sono chiamati quartili. Sono calcolati allo stesso modo - con un numero dispari di elementi, viene preso un numero che si trova nel mezzo di una riga e per pari - la metà della somma di due elementi centrali.

Esiste anche un grafico speciale in cui è possibile visualizzare tutti i valori del campione, il suo ambito, la mediana, l'intervallo tra i tre mesi e i valori anomali, valori che non rientrano nell'errore statistico. L'immagine risultante ha un nome molto specifico (e anche non matematico) - una scatola con i baffi.

distribuzione

La distribuzione si riferisce anche ai concetti di base della teoria della probabilità e della statistica matematica. In breve, è un riepilogo di tutte le variabili casuali che possiamo vedere come risultato del test. Il parametro principale qui è la probabilità di occorrenza di ciascun valore specifico.

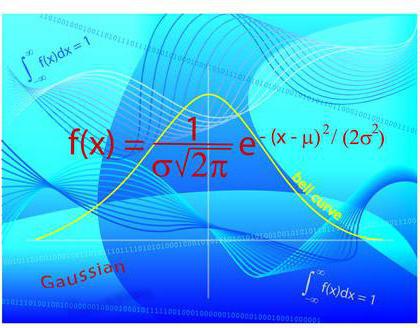
Una distribuzione normale è una che ha un picco centrale, in cui si trova il valore che si verifica più spesso. Da esso archi divergono risultati meno e meno probabili. In generale, il programma dal lato sembra una "diapositiva". In futuro imparerai che il teorema del limite centrale, fondamentale per la teoria della probabilità, è strettamente connesso a questo tipo di distribuzione. Descrive le leggi che sono importanti per i rami della matematica considerati da noi, che sono molto utili per una varietà di calcoli.

Ma torniamo all'argomento. Ci sono altri due tipi di distribuzione: asimmetrica e multimodale. Il primo assomiglia a una metà del grafico "normale", cioè l'arco scende solo in una direzione dal valore di picco. Infine, una distribuzione multimodale è una che ha diversi valori "superiori". Il programma, quindi, cade, quindi aumenta. Il valore di frequenza più elevato in qualsiasi distribuzione è chiamato modalità. È anche uno dei concetti base della teoria della probabilità e della statistica matematica.

Distribuzione gaussiana

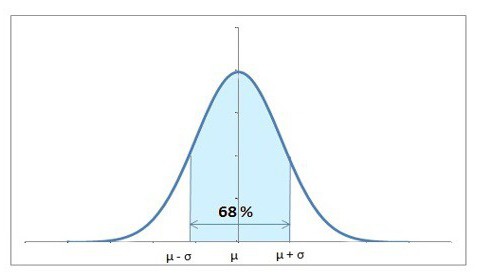
Una distribuzione gaussiana, o normale, è quella in cui la deviazione delle osservazioni dalla media obbedisce a una certa legge.

In breve, la dispersione principale dei valori campione tende in modo esponenziale alla modalità, la più frequente. Per parlare più precisamente, il 99,6% di tutti i valori si trova entro tre deviazioni standard (ricordate, abbiamo visto questo concetto sopra?).

La distribuzione gaussiana è uno dei concetti base della teoria della probabilità. Con l'aiuto di esso, è possibile capire se un elemento è incluso nella categoria di "tipico" secondo uno o un altro parametro - questo è il modo in cui l'altezza e il peso di una persona sono valutati in base all'età, al livello di sviluppo intellettuale, allo stato psicologico e molto altro.

Come applicare

È interessante notare che i dati matematici "noiosi" possono essere utilizzati a proprio vantaggio. Ad esempio, un giovane ha applicato la teoria della probabilità e le statistiche per vincere diversi milioni di dollari nella roulette. È vero, dovevamo prepararci per questo - nel corso di diversi mesi, abbiamo registrato i risultati dei giochi in vari casinò.

Dopo aver analizzato, ha scoperto che una delle tabelle è leggermente inclinata, il che significa che un numero di valori appare statisticamente significativamente più spesso di altri. Pochi calcoli, pazienza - e ora i proprietari dell'istituzione sono perplessi, pensando a come una persona può essere fortunata.

Ci sono molte attività quotidiane che non possono essere risolte senza ricorrere alle statistiche. Ad esempio, come determinare quanti negozi ordinare vestiti di diverse dimensioni: S, M, L, XL? Per fare questo, è necessario analizzare chi compra spesso vestiti in città, nella zona, nei negozi vicini. Se tali informazioni non vengono ottenute, il proprietario rischia di perdere molti soldi.

conclusione

Abbiamo preso in considerazione tutta una serie di concetti di base della teoria della probabilità: test, eventi, permutazioni e posizionamenti, aspettativa e varianza, modalità e distribuzione normale ... Inoltre, abbiamo esaminato un numero di formule a cui è stato dedicato più di un mese di studio.

Non dimenticare: la matematica è necessaria quando si studiano economia, scienze naturali, tecnologia dell'informazione, specialità ingegneristiche. Anche le statistiche come una delle sue aree qui non possono essere evitate.

Ora tocca a te: pratica, risolvi problemi ed esempi. Anche i concetti e le definizioni di base della teoria della probabilità saranno dimenticati, se non di dedicare tempo alla ripetizione. Inoltre, le seguenti formule si baseranno in gran parte su quelle che abbiamo considerato. Pertanto, cerca di ricordarli, soprattutto perché non ce ne sono così tanti.