Distribuzione binomiale: definizione, formula, esempi

La teoria della probabilità è invisibilmente presente nelle nostre vite. Non prestiamo attenzione a questo, ma ogni evento nella nostra vita ha una certa probabilità. Tenendo conto dell'enorme numero di scenari, diventa necessario per noi determinare il più probabile e meno probabile di essi. È molto più conveniente analizzare graficamente tali dati probabilistici. La distribuzione può aiutarci in questo. Binomiale: uno dei più facili e accurati.

Prima di passare direttamente alla matematica e alla teoria della probabilità, affrontiamo chi è arrivato per primo a questo tipo di distribuzione e qual è la storia dello sviluppo dell'apparato matematico per questo concetto.

Storia di

Il concetto di probabilità è stato conosciuto fin dai tempi antichi. Tuttavia, gli antichi matematici non hanno attribuito molta importanza ad esso e sono stati in grado di porre solo le basi per la teoria, che in seguito divenne la teoria della probabilità. Creavano alcuni metodi combinatori che aiutarono molto coloro che in seguito crearono e svilupparono la teoria stessa.

Nella seconda metà del diciassettesimo secolo iniziò la formazione dei concetti e dei metodi di base della teoria della probabilità. Sono state introdotte definizioni di variabili casuali, metodi per calcolare la probabilità di eventi semplici e alcuni eventi indipendenti e dipendenti complessi. Tale interesse per le variabili casuali e le probabilità è stato dettato dal gioco d'azzardo: tutti volevano sapere quali erano le sue possibilità di vincere il gioco.

Il passo successivo fu l'applicazione dei metodi nella teoria della probabilità analisi matematica. Eminenti matematici, come Laplace, Gauss, Poisson e Bernoulli, hanno assunto questo compito. Hanno avanzato questa area della matematica ad un nuovo livello. Fu James Bernoulli a scoprire la legge sulla distribuzione binomiale. A proposito, come scopriremo più tardi, molti altri sono stati fatti sulla base di questa scoperta, che ha reso possibile la creazione di una legge di distribuzione normale e molti altri.

Ora, prima di iniziare a descrivere la distribuzione del binomio, aggiorneremo un po 'i concetti della teoria della probabilità, probabilmente già dimenticati dalla scuola.

Fondamenti di teoria della probabilità

Considereremo tali sistemi, in conseguenza dei quali sono possibili solo due risultati: "successo" e "non successo". Questo è facile da capire con un esempio: gettiamo una moneta, facendo un'ipotesi che le code cadranno. Le probabilità di ciascuno degli eventi possibili (le code cadono - "successo", l'aquila si abbassa - "non successo") sono il 50% con bilanciamento perfetto della moneta e l'assenza di altri fattori che possono influenzare l'esperimento.

È stato l'evento più semplice Ma ci sono anche sistemi complessi in cui vengono eseguite azioni sequenziali e le probabilità dei risultati di queste azioni possono variare. Per esempio, considera un sistema del genere: in una scatola, il cui contenuto non possiamo vedere, ci sono sei sfere assolutamente identiche, tre paia di colori blu, rosso e bianco. Dobbiamo prendere alcune palle a caso. Di conseguenza, tirando prima una delle palline bianche, ridurremo a volte la probabilità che anche la prossima ottenga una palla bianca. Ciò accade perché il numero di oggetti nel sistema cambia.

Nella prossima sezione, esamineremo concetti matematici più complessi che ci conducono da vicino a ciò che le parole "distribuzione normale", "distribuzione binomiale" e "mi piace" significano.

Elementi di statistica matematica

Nella statistica, che è una delle aree di applicazione della teoria della probabilità, ci sono molti esempi in cui i dati per l'analisi non vengono forniti esplicitamente. Cioè, non in numeri, ma sotto forma di divisione secondo i segni, ad esempio, per sesso. Al fine di applicare un apparato matematico a tali dati e trarre conclusioni dai risultati ottenuti, è necessario convertire i dati originali in un formato numerico. Di norma, per ottenere ciò, a un risultato positivo viene assegnato il valore 1 e a uno negativo viene assegnato il valore 0. Quindi, otteniamo dati statistici che possono essere analizzati utilizzando metodi matematici.

Il prossimo passo nella comprensione di cosa sia una distribuzione binomiale di una variabile casuale è determinare la varianza della variabile casuale e l'aspettativa matematica. Questo è discusso nella prossima sezione.

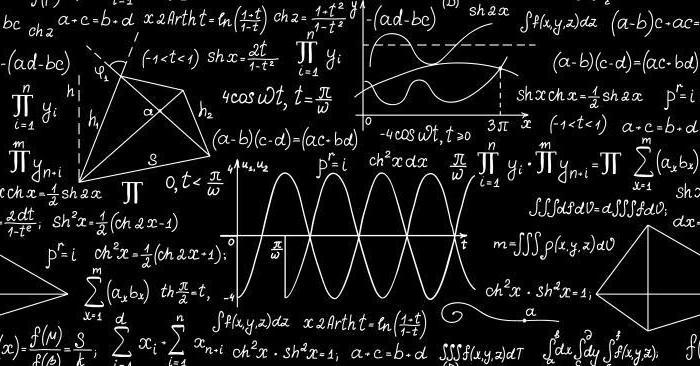
Aspettativa matematica

In effetti, è facile capire quale sia l'aspettativa. Considera un sistema in cui ci sono molti eventi diversi con le loro varie probabilità. L'aspettativa matematica sarà chiamata un valore uguale alla somma dei prodotti dei valori di questi eventi (e della forma matematica, che abbiamo discusso nell'ultima sezione) sulla probabilità della loro implementazione.

L'aspettativa matematica della distribuzione binomiale viene calcolata secondo lo stesso schema: prendiamo il valore di una variabile casuale, lo moltiplichiamo per la probabilità di un risultato positivo e quindi riepiloghiamo i dati ottenuti per tutte le grandezze. È molto conveniente presentare questi dati graficamente: è così che si percepisce meglio la differenza tra le aspettative matematiche di diverse quantità.

Nella prossima sezione, parleremo un po 'di un altro concetto: la varianza di una variabile casuale. È anche strettamente correlato a un concetto come la distribuzione di probabilità binomiale, ed è la sua caratteristica.

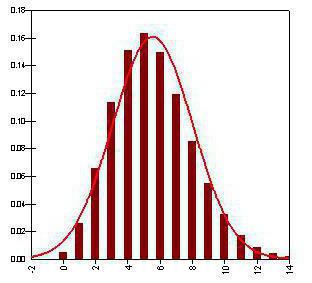
La varianza della distribuzione binomiale

Questo valore è strettamente correlato al precedente e caratterizza anche la distribuzione dei dati statistici. Rappresenta il quadrato medio delle deviazioni di valori dalle loro aspettative. Cioè, la varianza di una variabile casuale è la somma dei quadrati delle differenze tra il valore della variabile casuale e la sua aspettativa, moltiplicato per la probabilità di questo evento.

In generale, questo è tutto ciò che dobbiamo sapere sulla varianza per capire quale sia la distribuzione di probabilità binomiale. Passiamo ora direttamente al nostro argomento principale. Vale a dire, a cosa si cela dietro una frase apparentemente piuttosto complessa "legge di distribuzione binomiale".

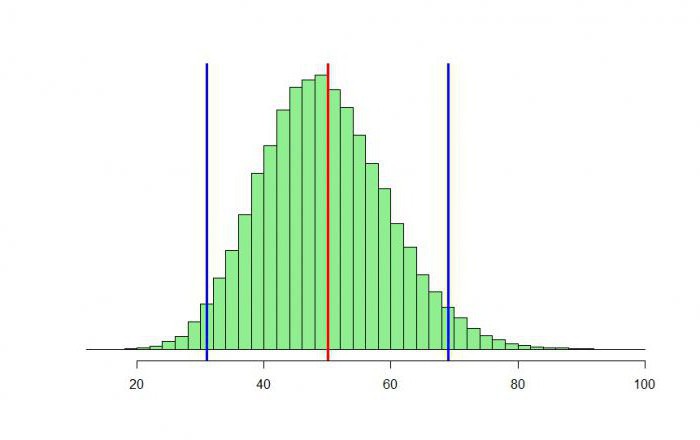
Distribuzione binomiale

Cerchiamo prima di capire perché questa distribuzione è binomiale. Viene dalla parola "bin". Forse avete sentito parlare del binomio di Newton - una formula con la quale potete scomporre la somma di due numeri arbitrari a e b in qualsiasi grado non negativo n.

Come probabilmente avete già intuito, la formula binomiale di Newton e la formula di distribuzione binomiale sono formule quasi identiche. Con la sola eccezione che il secondo ha un valore applicato per quantità specifiche, e il primo è solo uno strumento matematico generale, le cui applicazioni in pratica possono essere diverse.

Formule di distribuzione

La funzione di distribuzione binomiale può essere scritta come la somma dei seguenti membri:

(n! / (nk)! k!) * p ^k * q ^nk

Qui n è il numero di esperimenti random indipendenti, p è il numero di esiti positivi, q è il numero di esiti falliti, k è il numero dell'esperimento (può assumere valori da 0 a n),! - designazione del fattoriale, tale funzione di un numero il cui valore è uguale al prodotto di tutti i numeri che lo raggiungono (ad esempio, per il numero 4: 4! = 1 * 2 * 3 * 4 = 24).

Inoltre, la funzione di distribuzione binomiale può essere scritta come funzione beta incompleta. Tuttavia, questa è una definizione più complessa, che viene utilizzata solo per risolvere problemi statistici complessi.

La distribuzione binomiale, esempi di cui abbiamo considerato sopra, è uno dei tipi più semplici di distribuzioni nella teoria della probabilità. Esiste anche una distribuzione normale, che è un tipo di binomio. È usato più spesso e più semplicemente nei calcoli. C'è anche una distribuzione di Bernoulli, una distribuzione di Poisson, una distribuzione condizionale. Tutti loro caratterizzano graficamente le probabilità di un processo in condizioni diverse.

Nella prossima sezione, vedremo gli aspetti relativi all'uso di questo apparato matematico nella vita reale. A prima vista, ovviamente, sembra che questa sia un'altra cosa matematica, che, come al solito, non trova applicazione nella vita reale, e generalmente non è necessaria a nessuno tranne che ai matematici stessi. Tuttavia, questo è lontano dal caso. Dopo tutto, tutti i tipi di distribuzioni e le loro rappresentazioni grafiche sono state create esclusivamente per scopi pratici e non come un capriccio per gli scienziati.

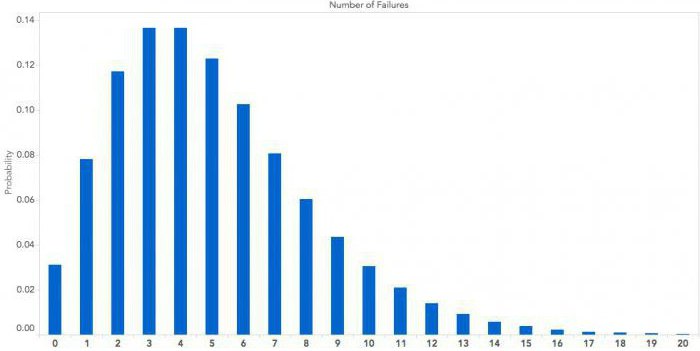
applicazione

Naturalmente, l'uso più importante della distribuzione si trova nelle statistiche, perché hanno bisogno di un'analisi completa dell'insieme di dati. Come mostra la pratica, molti array di dati hanno approssimativamente la stessa distribuzione di valori: le aree critiche di valori molto bassi e molto alti, di norma, contengono meno elementi rispetto ai valori medi.

L'analisi di grandi quantità di dati è richiesta non solo nelle statistiche. È indispensabile, per esempio, nella chimica fisica. In questa scienza, viene utilizzato per determinare molte delle quantità associate a oscillazioni e movimenti casuali di atomi e molecole.

Nella prossima sezione, vediamo quanto sia importante per te e me l'uso di concetti statistici come la distribuzione binomiale di una variabile casuale nella vita di tutti i giorni.

Perché ne ho bisogno?

Molte persone si pongono questa domanda quando si tratta di matematica. E a proposito, la matematica non è per niente chiamata la regina della scienza. È la base della fisica, della chimica, della biologia, dell'economia e in ciascuna di queste scienze si applica anche la distribuzione: se questa distribuzione binomiale discreta, o normale, non è importante. E se guardiamo da vicino il mondo che ci circonda, vedremo che la matematica è usata ovunque: nella vita di tutti i giorni, sul lavoro, e persino le relazioni umane possono essere rappresentate come dati statistici e analizzate (a proposito, quelli che lavorano in organizzazioni speciali che raccolgono informazioni).

Ora parliamo un po 'di cosa fare se hai bisogno di sapere molto di più su questo argomento rispetto a ciò che abbiamo delineato in questo articolo.

Cos'altro puoi leggere?

Le informazioni che abbiamo fornito in questo articolo sono lungi dall'essere complete. Ci sono molte sfumature riguardo a quale forma può assumere una distribuzione. La distribuzione binomiale, come abbiamo già scoperto, è uno dei principali tipi su cui si basano tutte le statistiche matematiche e la teoria della probabilità.

Se è diventato interessante per te, o in relazione al tuo lavoro, devi sapere molto di più su questo argomento, dovrai studiare letteratura specializzata. Dovremmo iniziare con il corso universitario di analisi matematica e andare alla sezione della teoria della probabilità. Sarà anche una conoscenza utile nel campo delle serie, perché la distribuzione della probabilità binomiale non è altro che una serie di membri consecutivi.

conclusione

Prima di finire l'articolo, vorremmo dire una cosa più interessante. Si riferisce direttamente al tema del nostro articolo e di tutta la matematica in generale.

Molte persone affermano che la matematica è una scienza inutile, e nulla di ciò che hanno vissuto a scuola è stato utile per loro. Ma la conoscenza non è mai superflua, e se qualcosa non ti è utile nella vita, significa che semplicemente non te ne ricordi. Se hai conoscenza, possono aiutarti, ma se non ci sono, allora non c'è bisogno di aspettare aiuto da loro.

Quindi, abbiamo esaminato il concetto di distribuzione binomiale e tutte le definizioni correlate e abbiamo parlato di come questo si applica alla nostra vita.