Accelerazione centripeta - produzione di formula e applicazione pratica

L'accelerazione centripeta ci accompagna ovunque. Che fa il nostro La Terra ruota intorno al sole. La gravità risultante ci consente di esistere su questo pianeta. Come si può capire cos'è l'accelerazione centripeta? Di seguito la definizione di questa quantità fisica.

osservazioni

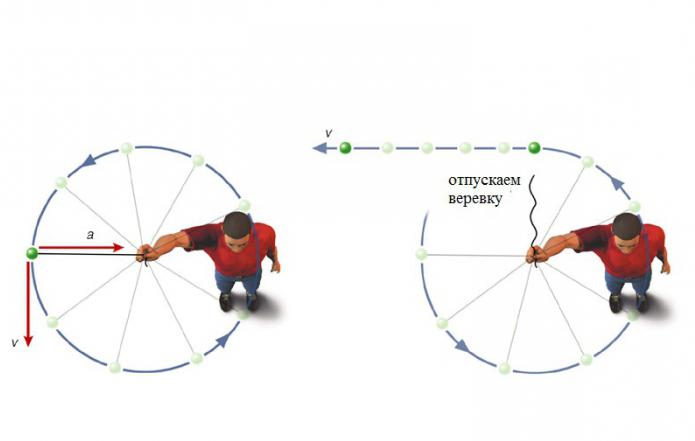
L'esempio più semplice di accelerazione di un corpo che si muove in un cerchio può essere osservato ruotando una pietra su una corda. Tiri la fune e la fune tira la pietra al centro. In ogni momento, la corda indica alla pietra una certa quantità di movimento, e ogni volta - in una nuova direzione. Potete immaginare il movimento della corda sotto forma di una serie di sobbalzi deboli. Un coglione - e la corda cambia direzione, un altro coglione - un altro cambio, e così via in un cerchio. Se rilasci improvvisamente la corda, i cretini si fermeranno e insieme a loro il cambio nella direzione della velocità si fermerà. La pietra si muoverà nella direzione della tangente al cerchio. La domanda sorge spontanea: "Con quale accelerazione il corpo si muoverà in questo istante?"

Formula di accelerazione centripeta

Prima di tutto, vale la pena notare che il movimento del corpo in un cerchio è difficile. Una pietra partecipa simultaneamente a due tipi di movimento: sotto l'azione di una forza, si muove verso il centro di rotazione, e allo stesso tempo tangenzialmente al cerchio, si allontana da questo centro. Secondo la seconda legge di Newton, la forza che tiene la pietra sulla corda è diretta verso il centro di rotazione lungo questa corda. Ci sarà anche diretto al vettore di accelerazione.

Lasciamo che per qualche tempo la nostra pietra, muovendosi uniformemente con la velocità V, arrivi dal punto A al punto B. Supponiamo che nel momento in cui il corpo ha attraversato il punto B, una forza centripeta abbia cessato di agire su di essa. Quindi per un periodo di tempo sarebbe caduto nel punto K. Si trova sulla tangente. Se nello stesso momento del tempo solo le forze centripete agissero sul corpo, allora durante il tempo t, muovendosi con la stessa accelerazione, apparirebbe nel punto O, che si trova su una linea retta, che rappresenta il diametro di un cerchio. Entrambi i segmenti sono vettori e obbediscono alla regola di aggiunta del vettore. Come risultato della somma di questi due movimenti nell'intervallo di tempo t, otteniamo il moto risultante lungo l'arco AB.

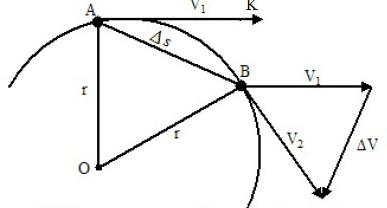
Se l'intervallo di tempo t è considerato trascurabile, allora l'arco AB sarà leggermente diverso dall'accordo AB. Pertanto, è possibile sostituire il movimento lungo un arco con un movimento lungo un accordo. In questo caso, il movimento della pietra lungo la corda obbedirà alle leggi del moto rettilineo, cioè la distanza percorsa AB sarà uguale al prodotto della velocità della pietra al momento del suo movimento. AB = V x t.

Indichiamo l'accelerazione centripeta desiderata dalla lettera a. Quindi il percorso coperto solo dall'azione dell'accelerazione centripeta può essere calcolato utilizzando la formula del moto uniformemente accelerato:

AO = 2/2.

La distanza AB è uguale al prodotto di velocità e tempo, cioè AB = V x t,

AO - precedentemente calcolato dalla formula movimento uniformemente accelerato muoversi in linea retta: AO = 2/2.

Sostituendo questi dati in una formula e trasformandola, otteniamo una formula di accelerazione centripeta semplice ed elegante:

a = v ² / R

Questo può essere espresso in parole come segue: l'accelerazione centripeta di un corpo che si muove in un cerchio è uguale al quoziente dal dividere la velocità lineare al quadrato del raggio del cerchio in cui il corpo ruota. La forza centripeta in questo caso sarà simile all'immagine qui sotto.

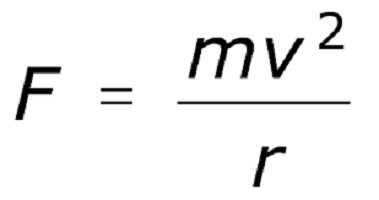
Velocità angolare

Velocità angolare uguale al quoziente della velocità lineare diviso per il raggio del cerchio. È vero anche il contrario: V = ωR, dove ω è la velocità angolare

Se si sostituisce questo valore nella formula, è possibile ottenere l'espressione dell'accelerazione centrifuga per la velocità angolare. Sembrerà così:

a = ω ² R.

Accelerazione senza cambiare velocità

Eppure, perché un corpo con accelerazione diretta verso il centro non si muove più velocemente e non si avvicina al centro di rotazione? La risposta sta proprio nella formulazione dell'accelerazione. I fatti suggeriscono che guidare in circolo è reale, ma per mantenerlo è necessaria l'accelerazione diretta verso il centro. Sotto l'azione di una forza causata da questa accelerazione, si verifica un cambiamento nella quantità di movimento, a seguito della quale la traiettoria del movimento si curva costantemente, cambiando la direzione del vettore di velocità tutto il tempo, ma non cambiando il suo valore assoluto. Muovendosi in cerchio, la nostra lunga e sofferta pietra si precipita verso l'interno, altrimenti continuerebbe a muoversi su una tangente. Ogni momento del tempo, lasciando una tangente, la pietra è attratta dal centro, ma non vi cade dentro. Un altro esempio di accelerazione centripeta può essere uno sciatore d'acqua, che descrive piccoli cerchi sull'acqua. La figura dell'atleta è inclinata; sembra cadere, continuando a muoversi e sporgendosi in avanti.

Quindi, possiamo concludere che l'accelerazione non aumenta la velocità del corpo, poiché i vettori di velocità e accelerazione sono perpendicolari tra loro. Aggiungendo al vettore di velocità, l'accelerazione cambia solo la direzione del movimento e mantiene il corpo in orbita.

Eccesso margine di sicurezza

Nella precedente esperienza ci siamo occupati della corda ideale, che non è stata strappata. Ma, diciamo, la nostra corda è la più comune, e puoi persino calcolare lo sforzo, dopo il quale si romperà semplicemente. Per calcolare questa forza, è sufficiente confrontare il margine di sicurezza della corda con il carico che sperimenta nel processo di rotazione della pietra. Ruotando la pietra a una velocità maggiore, gli dai più movimento, il che significa maggiore accelerazione.

Con un diametro della fune di iuta di circa 20 mm, la sua resistenza alla trazione è di circa 26 kN. È interessante notare che la lunghezza della corda non appare da nessuna parte. Ruotando un carico di 1 kg su una fune con un raggio di 1 m, si può calcolare che la velocità lineare necessaria per romperla è 26 x 10 ³ = 1 kg x V 2/1 m. Pertanto, la velocità che è pericolosa superare sarà √ 26 x 10 ³ = 161 m / s.

gravità

Considerando l'esperienza, abbiamo trascurato l'azione la forza di gravità, poiché a velocità così elevate la sua influenza è trascurabile. Ma puoi vedere che quando si svolge una lunga corda, il corpo descrive una traiettoria più complessa e si avvicina gradualmente al terreno.

Corpi celesti

Se trasferiamo le leggi del moto lungo un cerchio nello spazio e le applichiamo al movimento corpi celesti È possibile riaprire diverse formule note da lungo tempo. Ad esempio, la forza con cui un corpo è attratto dalla Terra è conosciuta con la formula:

F = m * g.

Nel nostro caso, il fattore g è l'accelerazione molto centripeta, derivata dalla formula precedente. Solo in questo caso, il ruolo della pietra sarà eseguito dal corpo celeste, attratto dalla Terra, e il ruolo della corda sarà la forza di gravità. Il moltiplicatore g sarà espresso attraverso il raggio del nostro pianeta e la velocità della sua rotazione.

risultati

L'essenza dell'accelerazione centripeta consiste in un duro e ingrato lavoro di tenere un corpo in movimento in orbita. C'è un caso paradossale quando, con un'accelerazione costante, il corpo non cambia la grandezza della sua velocità. Per la mente non allenata, una tale affermazione è piuttosto paradossale. Tuttavia, nel calcolo del moto di un elettrone attorno al nucleo e nel calcolo della velocità di rotazione di una stella attorno a un buco nero, l'accelerazione centripeta non gioca l'ultimo ruolo.