Combinatorics - che cos'è? Elementi di combinatoria
Specialisti in vari campi devono risolvere problemi combinatori: riorganizzazione di numeri, segni e altri oggetti. Ad esempio, il capo del negozio deve distribuire diversi tipi di lavoro tra le macchine funzionanti. Combinatorics è un ramo significativo della matematica, che, come non è difficile indovinare, trova la sua nicchia in vari campi e specialità: fisica, biologia, linguistica, chimica, ingegneria, teoria della codifica e molto altro. I principi della combinatoria sono anche alla base della soluzione di un insieme di problemi probabilistici.
Storia di
I primi prerequisiti di combinatoria come scienza apparvero nel 16 ° secolo. Contribuito allo sviluppo di questa area di conoscenza in larga misura, il fascino della gente per il gioco d'azzardo: carte, dadi, lotteria perse non solo oro e gioielli, ma palazzi e proprietà. Pertanto, chiedendo, per esempio, su quanto spesso si possa gettare una buona serie di punti sulle ossa o ottenere due assi, le persone gradualmente hanno raggiunto le basi della combinatoria e della probabilità. I combinatorici hanno aiutato qualcuno a vincere di più o a perdere di meno? La domanda è interessante, ma la sua considerazione va oltre lo scopo di questo articolo.

Il primo matematico che si interessò attivamente al combinatorismo fu l'italiano italiano Tartaglia (1499-1557), dopo di lui, eminenti scienziati come Pascal, Fermat, Bernoulli, Leibnitz, Eulero e altri attivamente immersi nello studio di queste domande, ma vale la pena notare che combinatorics su Rimaneva ancora, se non un gioco divertente con numeri, quindi una teoria che viene utilizzata esclusivamente nel gioco d'azzardo e non ha il diritto di essere utilizzata altrove.
Lo sviluppo della combinatoria
Progressi significativi nella combinatoria sono avvenuti con l'avvento del 20 ° secolo. computer, programmazione e, soprattutto, matematica discreta. Durante questo periodo, la combinatoria raggiunge il culmine del suo rapido sviluppo e diventa una scienza a tutti gli effetti. I metodi combinatori stanno cominciando ad essere usati ovunque:
- soluzione dei problemi di trasporto;
- scheduling;
- preparazione di piani per la produzione e la vendita di beni;
- nella teoria dei processi casuali;
- in statistica matematica e teoria della probabilità;
- nella preparazione e nella conduzione di esperimenti;
- negli scacchi;
- in termodinamica;
- in geometria;
- e in molte altre aree.
Sfida leader superstiziosa
C'era un leader nel mondo che credeva che il numero 8 gli portasse un totale fallimento. Pertanto, ha deciso di sbarazzarsi di tutti i numeri che conterrebbero la figura otto. 600 persone hanno lavorato sotto la sua supervisione. Tutti avevano numero di identificazione passare per lavoro, composto da tre numeri. Senza pensarci due volte, il manager ha deciso di escludere il numero 8 dal numero di passaggi e poi si è chiesto se ci fossero abbastanza numeri diversi per 600 persone nell'intervallo da 000 a 999, che non includerebbe 8?
La soluzione ovvia a questo problema è di scrivere manualmente tutti i numeri da 000 a 999 e cancellare quelli in cui ci sono otto. È possibile risolvere il problema in modo più semplice? Se, per 999 numeri, è possibile eseguire l'operazione con l'elenco di tutte le varianti, l'intervallo da 000000 a 999999 richiederà uno sforzo molto maggiore. È quello di risparmiare tempo e fatica per combinare formule progettate.
La soluzione al problema del leader superstizioso
Un'altra soluzione è la seguente. Eliminando 8 dalla serie, otteniamo che 0, 1, 2, 3, 4, 5, 6, 7, 9 - questi nove numeri sono validi. Dopodiché, dovresti trovare tutti i numeri a due cifre che non contengono 8. Questo è fatto semplicemente: devi prendere qualsiasi numero dal valido e aggiungere ad esso anche qualsiasi numero dal valido. Quindi, otterremo facilmente tutti i numeri a due cifre che si adattano alla condizione. Di conseguenza, otteniamo che ogni singola cifra fornisca 9 diversi numeri a due cifre. Il numero totale di tali cifre sarà 9 * 9 = 9 2 = 81.
Continuando l'analogia, possiamo concludere che per ottenere tutti i numeri a tre cifre senza otto, è necessario assegnare una terza cifra ai numeri a due cifre esistenti, anche dai valori consentiti. Poi otteniamo che il numero di tali cifre sarà 9 2 * 9 = 9 * 9 * 9 = 729. Così, abbiamo scoperto che il capo del nostro manager sarebbe stato in grado di fornire 600 dipendenti con lacune, che i numeri non avrebbero contenuto 8. Provare a risolvere il problema per conto proprio con numeri a cinque cifre.
E cosa succederà se al manager non piace il numero 2? Risulta, quindi il numero di numeri ammissibili sarà 8, vale a dire: 0, 1, 3, 4, 5, 6, 7, 9. Quindi, avendo stimato il numero di combinazioni di numeri senza 2 e 8, possiamo concludere che il loro numero è 8 * 8 * 8 = 512, e questo non è chiaramente sufficiente per fornire 600 persone con pass. Combinatorics è una scienza che aiuta a rispondere a tali domande in modo più efficace di quanto possa essere fatto con la forza bruta.
Problema del lotto
Tutti conoscono il gioco. C'è una borsa in cui si trovano barili con numeri da 1 a 90. I biglietti sono distribuiti a tutti i partecipanti, in cui è necessario dipingere un certo numero di celle con numeri. Dopodiché, il lotto principale esce dalla borsa uno dei barili numerati. Il vincitore sarà colui che ha cancellato la maggior parte dei numeri nel biglietto, che coincide con quelli che l'host del gioco ha tirato fuori.

Una volta che Nina, giocando al lotto, pensò. Guardava spesso mentre il presentatore ottiene lo stesso numero dalla borsa. Ma allo stesso tempo, i primi due barili si sono rivelati gli stessi molto meno spesso. Poi si chiedeva in quanti modi si potevano ottenere due barili in modo coerente dalla borsa? Elementi di combinatoria aiutano a rispondere alla sua domanda.
Soluzione del Lotto
Ovviamente, il primo barile può avere numeri da 1 a 90. In altre parole, ci sono 90 modi per estrarre il primo barile. Ma che ne dici di questo? Se, ad esempio, un fusto n. 63 è stato rimosso da una borsa, nel gioco corrente non si ripeterà più.
Il metodo della tabella ci aiuterà a risolvere il problema. Dove nel titolo e nella colonna di intestazione verranno scritti i numeri da 1 a 90. Così, all'intersezione di una qualsiasi riga e di qualsiasi colonna ci sarà una coppia di numeri, o un paio di barili rimossi dal sacchetto. Allo stesso tempo sulla diagonale del tavolo si troveranno le stesse coppie di numeri. Il che è impossibile in base alla condizione, poiché dopo aver rimosso una singola cifra dalla borsa, la sua ripetizione è impossibile. Ottieni una tabella con il seguente modulo:
| 1 | 2 | ... | 90 | |
| 1 | x | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | x | ... | 2, 90 |
| ... | ... | ... | x | ... |
| 90 | 90, 1 | 90, 2 | ... | x |
Totale otteniamo la tabella, in cui il numero di celle è 90 * 90 = 8100. Va ricordato che ci sono 90 coppie di cifre situate sulla diagonale, che sono impossibili secondo le condizioni. Quindi la risposta alla domanda su quanti modi si possono ottenere 2 barili dalla borsa saranno 8100 - 90 = 8010 opzioni.
Ragionando in un modo leggermente diverso puoi arrivare alla stessa risposta. Per il primo barile ci sono 90 opzioni. Dopo che il primo è stato estratto, resteranno 89 opzioni per il secondo barile. Pertanto, il numero totale di opzioni sarà 90 * 89 = 8010. Gli elementi di combinatoria possono essere utilizzati in modi diversi. L'unica domanda è la semplicità e l'universalità del metodo. Ad esempio, il metodo table può essere utilizzato per tre barili da estrarre in una riga e, ovviamente, questo sarà il limite. E per quattro o più?
Problema dell'equipaggio
Se le scelte dipendono da quali oggetti sono stati selezionati in precedenza, allora è conveniente visualizzare un tale processo come un "albero". Nel primo passaggio, poiché molte linee sono disposte da un punto in quanto vi sono possibili scelte nel primo passaggio. Alla fine di ogni riga ci sono anche tante linee aggiuntive che possono essere fatte nel secondo passo, ecc. Di conseguenza, verrà disegnato un tipo di albero o grafico. Combinatorio e teoria possono sembrare piuttosto confusi e incomprensibili, quindi diamo un'occhiata a un esempio.
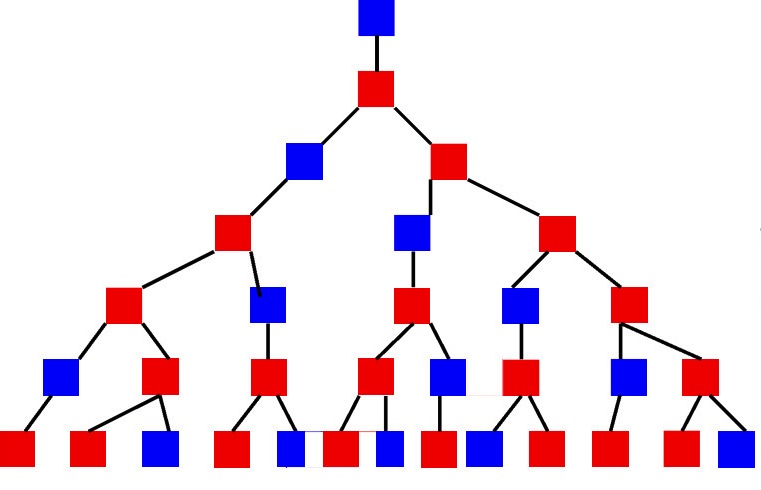
Prima dell'inizio dell'anno di spedizione, la dirigenza ha un compito: raccogliere gli equipaggi per i viaggi. Ogni squadra deve includere tre persone: un comandante, un ingegnere e un medico. Allo stesso tempo, il numero di specialisti in una particolare area può variare. È permesso, ad esempio, che un medico venga inviato a due diverse spedizioni, dal momento che ci sono solo due medici e che possono esserci tre per comandante e ingegnere. In questo caso, il compilatore del piano di spedizione deve tenere conto della compatibilità psicologica dei membri del team. Questa caratteristica è una delle più importanti nelle spedizioni lunghe e lontane per la loro condotta di successo. Sulla base di tutte le condizioni descritte, emerge il seguente quadro:
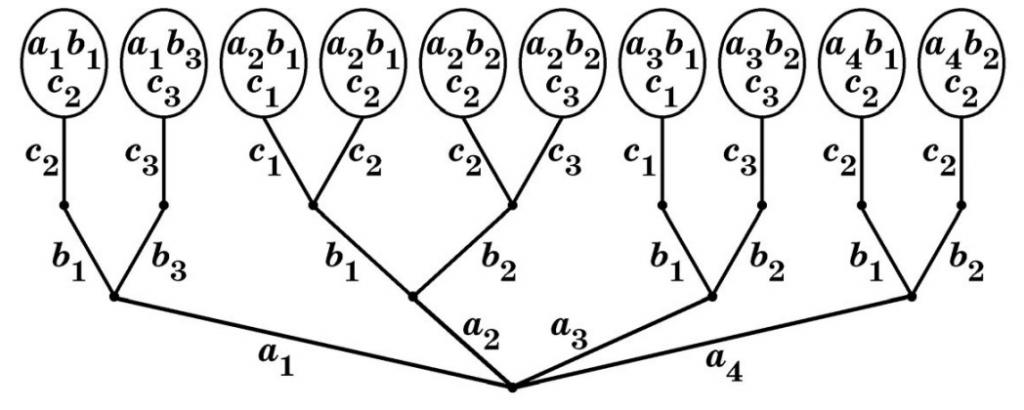
Dove io sono i comandanti, io sono gli ingegneri e io sono i dottori. Allo stesso tempo, durante il test di ciascuna persona, è stato scoperto che il comandante 1 si comporta psicologicamente bene con gli ingegneri b 1 e b 3 , a 2 - con b 1 eb 2 , ma il medico c 3 è incompatibile con l'ingegnere b 1 , ecc. La domanda che era originariamente posta al project manager era quanti membri dell'equipaggio possono essere composti in tali condizioni. Dal grafico, si può vedere che ci possono essere 10 equipaggi in totale. Ma cosa sarebbe successo se la questione della compatibilità psicologica non avesse peso? Poi si scopre che dopo la scelta dei comandanti a i , ci sarebbero 3 alternative per ognuna di esse nella scelta di un ingegnere. Di conseguenza, per una coppia di comandante e ingegnere, ci sarebbero anche 3 opzioni per i medici. Quindi il numero di combinazioni raggiungerà 4 * 3 * 3 = 36 membri dell'equipaggio.
Posizionamenti, permutazioni e combinazioni
Negli esempi sopra, la soluzione dei problemi si è verificata con il cosiddetto metodo assiomatico. Cioè, si può dire che ci sono una serie di compiti di base, la cui soluzione può essere ridotta a molti problemi. Tuttavia, proprio come nella stereometria, è scomodo risolvere problemi basati esclusivamente su assiomi, e per questo è usato uno strumento più conveniente chiamato "teoremi", quindi in combinatoria è più conveniente usare metodi più generalizzati e comprovati. Nel corso di uno studio secolare di combinatoria, divenne ovvio che un numero di compiti si incontrarono più spesso di altri, e furono separati in classi separate e ottennero il loro nome, diventando i principali combinatori - vale a dire posizionamenti, permutazioni e combinazioni.

Problemi combinatori
Uno dei problemi chiave dei metodi combinatori è determinare quale serie di compiti dovrebbe essere considerata combinatoria. Questo non può essere definito in modo preciso a causa dell'ampia varietà di problemi che rientrano nella categoria combinatoria. E poi, molti compiti possono riguardare sia la combinatoria, sia un'altra area, essendo contigua o borderline.

Nel caso semplificato, si può notare che la matematica combinatoria include problemi che coinvolgono campioni e posizioni di oggetti. Allo stesso tempo, la combinatoria è caratterizzata dal lavorare esclusivamente con un insieme finito di oggetti. Sulla base di queste disposizioni, possiamo distinguere i seguenti compiti caratteristici della combinatoria:
- Crea una selezione di oggetti, tenendo conto di eventuali proprietà.
- Dimostrare o confutare l'esistenza di un campione in determinate condizioni.
- Trova il numero di combinazioni possibili.
- Trova tutte le combinazioni e determina l'algoritmo per la loro enumerazione.
- Trova la soluzione ottimale di un problema in determinate condizioni.
Se il problema in questione può essere assegnato a uno di questi tipi, allora è combinatorio e le formule combinatorie aiuteranno a risolverlo.