Numeri complessi e azioni su di loro

I numeri complessi , nel senso tradizionale del termine, non sono numeri usati nel conteggio e nella misurazione, ma sono oggetti matematici che sono definiti dalle proprietà presentate di seguito.

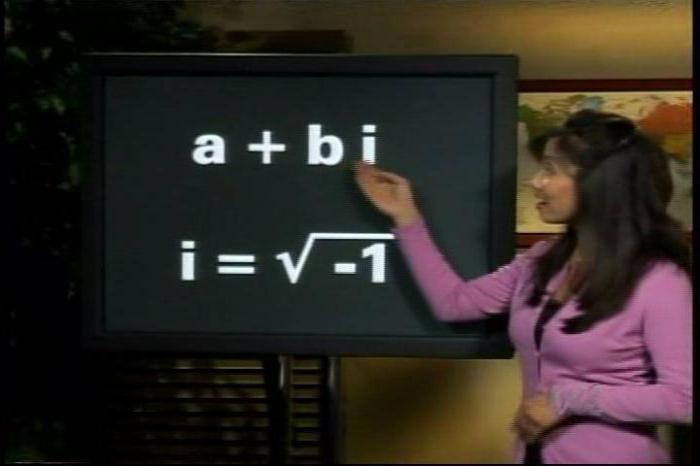
Utilizzare 3 forme di un numero complesso: algebrico, esponenziale, trigonometrico.

Forma algebrica

I numeri complessi sono designati dall'espressione ω + νi, dove ω e ν sono reali, e il simbolo i , è determinato dalla condizione i ² - 1 - l'unità è immaginaria.

Di conseguenza, il numero complesso ω + νi è diviso in parti reali e immaginarie. Per comodità, è raffigurato in una lettera (ad esempio, η ): η = ω + νi .

Le parti del numero complesso η = ω + νi , reale e immaginario, sono denotate da ω = Reη, ν = Itη, rispettivamente.

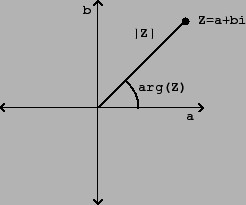
I numeri complessi sono considerati uguali quando le loro parti reali e immaginarie sono equivalenti. Un numero complesso è considerato uguale a zero se le sue parti, reali e immaginarie, sono uguali a zero.

Operazioni aritmetiche

aggiunta

La somma di numeri complessi è un numero complesso, la cui parte reale è equivalente alla somma di parti reali e quella immaginaria è equivalente alla somma di parti immaginarie:

η = (ω ₁ + ω ₂ ) + (ν ₁ + ν ₂ ) i.

Si dice che tra il complesso η abbiamo guadagnato aggiungendo i numeri del complesso :

η = η ₁ + η _2.

Il complesso η ₁ e η _{2 sono} indicati come termini.

Le leggi dell'operazione di aggiunta:

1) la legge di associatività;

2) la commutatività .

Il numero complesso -ω-bi è chiamato il numero complesso ω + νi opposto. La somma dei numeri complessi opposti è zero.

differenza

La differenza tra numeri complessi è chiamata il numero complesso η uguale alla somma del numero η ₁ e il numero opposto η ₂ :

η = η ₁ + (- η ₂ ) = (ω ₁ -ω ₂ ) + (ν ₁ -ν ₂ ) i.

Si dice che il numero del complesso η sia stato acquisito sottraendo η ₂ e η ₁ (numeri complessi), ed è scritto:

η = η ₂ -η ₁ .

prodotto

Il prodotto di numeri complessi è un numero complesso:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i.

Si dice che il numero del complesso η sia stato ottenuto moltiplicando η ₁ per η ₂ (i numeri η ₁ e η ₂ sono complessi) e scrivono:

η = η ₁ η ₂ .

Il complesso η ₁ e η _{2 sono} chiamati moltiplicatori.

Le leggi della moltiplicazione dei numeri complessi:

1) la legge di associatività ;

2) la commutatività .

divisione

I particolari numeri complessi sono chiamati complessi η tali che η ₁ = η _1: η ₂ ( η2 0 ) . I numeri complessi privati ​​sono calcolati dalla formula:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) / (ω ² + ν ² ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i / (ω ² + ν ² ).

Si dice che il numero η sia stato ottenuto dividendo η ₁ per η ₂ , ed è scritto:

η = η ₁ / η _{2 .}

L'aggiunta e la moltiplicazione di numeri complessi sono collegati da una regola chiamata legge di moltiplicazione distributiva riguardante l'aggiunta .

Numeri complessi trigonometrici

Usa anche un'altra forma di registrazione di numeri complessi, che è chiamata trigonometrica.

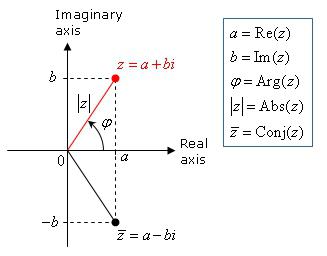
Il numero complesso ω + νi può essere scritto come:

η = k (cosβ + isinβ), dove k ² = ω ² + ν ² .

Questa espressione è una forma di registrazione di numeri complessi, che è chiamata trigonometrica. Il modulo di un numero complesso è un numero reale k , e l'angolo β , misurato in radianti, è il suo argomento.

Se il numero complesso non è zero, allora il suo modulo è positivo; se η = 0 , in altre parole, ω = ν = 0 , allora il suo modulo è uguale a zero. Il modulo è definito in modo univoco.

Il prodotto di numeri complessi trigonometrici è il modulo del numero complesso, che è equivalente al prodotto di fattori, o meglio, i loro moduli, e l'argomento è equivalente alla somma degli argomenti dei fattori:

η ₁ η ₂ = k ₁ k ₂ [cos (β ₁ + β ₂ ) + isin (β ₁ + β ₂ )].

I numeri complessi trigonometrici privati, che non sono zero, sono un numero complesso, il cui modulo è equivalente al dividendo parziale e al divisore (dei loro moduli), e l'argomento equivale alla differenza degli argomenti del dividendo e del divisore:

η ₁ / η ₂ = k ₁ / k ₂ [cos (β ₁ -β ₂ ) + isin (β ₁ -β ₂ )].

Il grado naturale del numero di complessi

In matematica, l' ennesima potenza del complesso η è il complesso w trovato come risultato della moltiplicazione η del complesso n volte da solo: w = ηη ... η .

Di solito usa una voce più breve:

w = η ⁿ ,

in cui il numero η è la base del grado e n (il numero naturale) è l'esponente.

L'ennesima potenza di η (numero complesso), che è data in forma trigonometrica, è calcolata dalla formula:

η ⁿ = k ⁿ (cosnβ + isinnβ).

Questa formula è chiamata la formula di Moivre.