Tipo di dati: array. È semplice ed elegante

Nella programmazione, si incontrano spesso tipi di dati come gli array. Questa è la soluzione più semplice quando si eseguono operazioni simili con un numero elevato di variabili dello stesso tipo. Se si tenta di scrivere un programma che includerà tutti questi dati e calcoli ripetitivi, è più opportuno includere nel prodotto una struttura chiamata matrice o matrice.

Il concetto generale di array

Sotto la matrice (un po 'più facile presentarlo sotto forma di tabella) è intesa come una sequenza di celle di memoria in cui sono memorizzate variabili dello stesso tipo. In questo caso, la relazione tra i dati e la struttura viene eseguita attraverso un nome e l'indice specificato. Aiuta a determinare quale variabile utilizzare quando si risolve un problema.

Dovrebbe essere chiaro che l'indice non è il contenuto della cella. Indica solo i dati contenuti in una particolare cella.

La definizione di tale struttura sarà la seguente: gli array sono un gruppo di dati dello stesso tipo che hanno il proprio nome e memorizzano le variabili in celle di memoria consecutive.

Esistono due tipi di matrici: una struttura (lineare) monodimensionale e una matrice bidimensionale. Il primo tipo è presentato sotto forma di tabella con una sola riga o una colonna. Nel caso specifico, il numero di indici indica la dimensione della matrice.

Un array bidimensionale è una struttura rappresentata come una tabella in cui il numero di riga indica il primo indice e il numero di colonna indica il secondo. Pertanto, nella matrice A (m, n), l'elemento dell'array a ₂₃ mostra che questa variabile si trova sulla seconda riga e nella terza colonna. E m imposta il numero di righe e n - il numero di colonne. Esiste una matrice quadrata (dove il numero di righe e colonne è uguale) e una rettangolare.

Matrici nella programmazione

Abbiamo già scoperto che gli array sono una raccolta di elementi dello stesso tipo. e tipo di dati deve essere uguale per tutto il tavolo Ogni struttura può avere un tipo di dati completamente diverso: numerico, stringa, carattere.

Quando si scrive un programma, è possibile impostare i limiti in due modi:

• utilizzando un nome di tipo in cui il primo e l'ultimo valore è un delimitatore;
• utilizzando costanti precedentemente dichiarate.

La struttura può anche essere definita in diversi modi. Vorrei sottolineare che ogni linguaggio del programma ha una propria sintassi. Ma il principio di creare una matrice è simile. Nel primo caso, viene richiamato un elemento specifico usando il nome della variabile della struttura e l'indice indicato tra parentesi quadre. In un altro caso, la matrice può essere specificata semplicemente elencando tutti gli elementi.

Non confondere il concetto di "indice" e "tipo di indice". La prima definizione è indicata nella sezione istruzioni per essere in grado di designare un elemento specifico dell'array. E il tipo di indice è usato solo nella sezione di descrizione della struttura. La dimensione dell'array è specificata nella descrizione. È altamente indesiderabile cambiare il numero di elementi nel processo di lavoro sul programma.

È possibile riempire le matrici con i dati in programmazione nei seguenti modi:

• tramite immissione manuale della tastiera;
• usando un generatore di numeri casuali;
• quando si dichiara una matrice come costante;
• dalla formula data.

Strutturazione di array

Le matrici sono un tipo di dati strutturato. Come già accennato, la matrice (se è bidimensionale) consiste in un numero finito di righe e colonne; se è lineare, è da una riga o da una colonna, dove anche il numero di elementi è limitato.

L'intersezione di una riga e una colonna è detta cella. Contiene variabili specifiche. Non è consentito avere diversi tipi di dati in una tabella. Gli elementi dell'array sono variabili con indici (indipendentemente dal fatto che la struttura sia lineare o bidimensionale). L'indice è il numero di una cella specifica. Lui indica la sua posizione nel tavolo.

Operazioni di matrice: aggiunta

Quindi, la matrice di dati che in matematica, quella in informatica, è un insieme di variabili. Puoi eseguire varie operazioni con esso: addizione, sottrazione, trasposizione, moltiplicazione, divisione.

Quando si aggiunge è necessario tener conto del fatto che la dimensione di entrambe le strutture dovrebbe essere la stessa. In questo caso, se le matrici A e B sono date con dimensione MxN, allora gli elementi C = A + B risultanti saranno c [i, j] = a [i, j] + b [i, j]. Si scopre che le variabili sono aggiunte elementwise.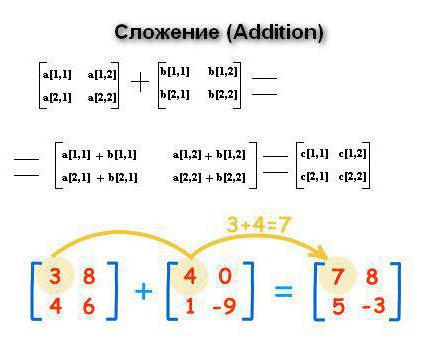

Operazioni dell'array: sottrazione

Questo punto, forse, dovrebbe essere avviato con la rimozione del segno meno dalla matrice (o, al contrario, introduzione). Ci sono casi in cui l'array di dati è costituito da elementi, molti dei quali sono negativi. In una tale situazione, sarebbe preferibile spostare il meno dalla struttura. Per fare ciò, un segno negativo viene posto davanti alla tabella e ogni elemento ha il segno invertito. Zero in questo caso è neutrale: non ha segno positivo o negativo.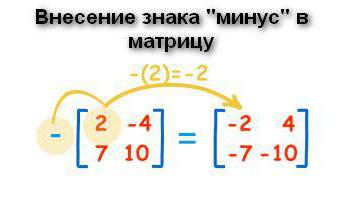

La sottrazione viene eseguita con lo stesso principio dell'aggiunta. Una variabile con lo stesso indice di un'altra struttura viene sottratta dal primo elemento della matrice. La risposta è registrata nella terza tabella nella posizione corrispondente.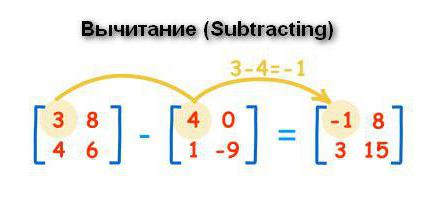

Operazioni di matrice: moltiplicazione e divisione

Oltre all'addizione e alla sottrazione, una serie di numeri può essere moltiplicata per un numero, moltiplicare le due strutture insieme, dividere l'una per l'altra.

Per trovare il prodotto della matrice e il numero, è necessario moltiplicare ogni elemento dell'array per l'elemento specificato. La risposta viene registrata in una cella con lo stesso indice della variabile originale. 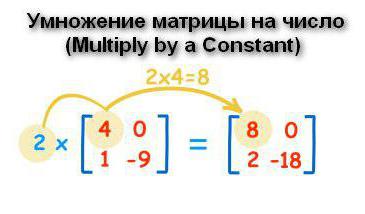Per moltiplicare due matrici l'una con l'altra, è necessario aderire al seguente algoritmo.

• Il numero di colonne nella prima tabella è uguale al numero di righe del secondo moltiplicatore. In questo caso, la dimensione della matrice risultante sarà la seguente: il numero di righe sarà uguale al numero di righe del primo fattore e il numero di colonne sarà uguale al loro numero dal secondo fattore.

• Considera due fattori.

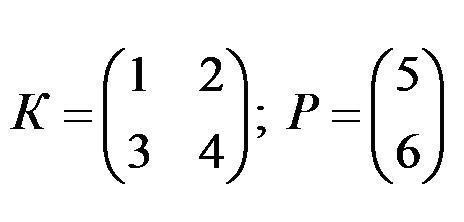
• Poiché il numero di colonne nel fattore K è uguale al numero di righe nell'array P, l'operazione è possibile. Ma se scambi le matrici in luoghi, allora la legge sulla modifica dei luoghi dei moltiplicatori non funziona qui. Pertanto, P x K è una voce non valida. Se entrambe le matrici sono quadrate, l'operazione è possibile in entrambi i casi.

La formula di moltiplicazione è la seguente.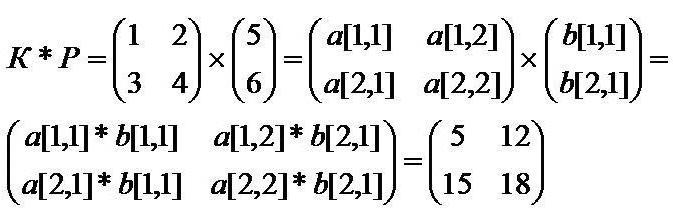

Se entrambi i fattori sono bidimensionali, è necessario seguire il principio mostrato nell'illustrazione seguente.

La divisione viene eseguita secondo la seguente formula. 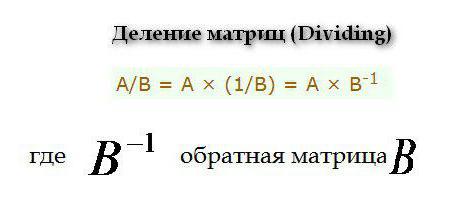Dove trovare la matrice inversa (inversione) viene eseguita secondo la seguente formula.

trasposizione

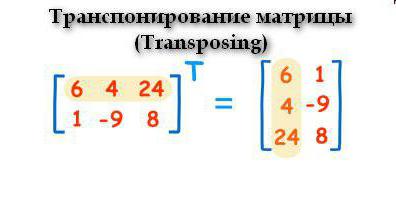
Questa operazione viene eseguita secondo il seguente principio: le righe diventano colonne. Sembra così