Arrotondamento decimale: apprendimento della matematica

Quindi, ora vedremo con te come avviene l'arrotondamento decimale. In realtà, questo processo non è così complicato come potrebbe sembrare a prima vista. È vero, alcuni scolari hanno difficoltà con questo argomento. Cerchiamo di aiutarli a capire la nostra domanda di oggi.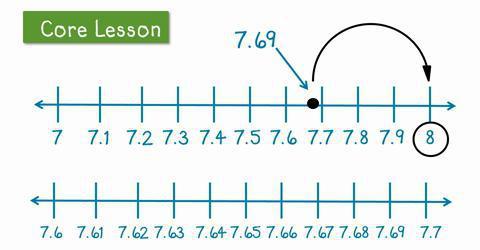

Concetto di frazione decimale

Prima dell'arrotondamento decimali, dobbiamo capire chiaramente cosa dobbiamo affrontare. Quanto meglio comprendiamo questa domanda con te, tanto più facile sarà in futuro.

In generale, il concetto di "frazione decimale" è rivelato nel 5 ° grado della scuola. Questo è un tipo di numero, costituito da una parte intera e da un numero frazionario, il cui denominatore è 10.

Per capire chiaramente cosa è in gioco, guardiamo un esempio e poi esaminiamo come avvengono i decimali di arrotondamento. Questo tipo di record sarà simile a questo: 5,26852. Se traduci il numero risultante in una frazione, puoi vedere quanto segue: 526852/100000. Le frazioni decimali possono essere sia positive che negative. Questo è tutto. Ora andiamo con te al nostro problema.

In alcune parti

Il punto è che l'arrotondamento delle frazioni decimali (grado 6), di norma, si verifica in parti. Innanzitutto, occupano il resto ("coda"), cioè i numeri che seguono la virgola. Solo allora può essere preso per l'intera parte.

La prima cosa che ci viene richiesta è determinare l'accuratezza con cui arrotonderemo le frazioni decimali. Fino a decimi, centesimi, millesimi e così via. Quindi devi seguire alcune regole e apprendere un punto importante che ti aiuterà sicuramente a far fronte al compito. Lasciaci lavorare con te con un chiaro esempio. Prendi un numero arbitrario: 78,9563245. È su di esso che testeremo con te la regola per arrotondare i decimali. Adesso lo conosciamo.

Regola principale

Il principio base che dobbiamo imparare è come sostituire i numeri durante l'arrotondamento. Il fatto è che è abbastanza facile da fare. Vediamo esattamente come.

Se hai 0, 1, 2, 3 o 4 come cifra, questa viene automaticamente sostituita con 0 e scartata. Quindi, avvicinati alla parte intera e guarda il prossimo numero.

Non appena la cifra nella cifra è 5, 6, 7, 8 o 9, dovrai scartare questa parte e aggiungerne una alla successiva (più vicina alla parte intera). Questo processo deve essere ripetuto fino alla precisione scelta dell'arrotondamento. Diamo ora un'occhiata a un esempio con te. Su di esso tutto apparirà più chiaro.

esempio

Quindi, iniziamo a arrotondare i decimali con te. Lavoriamo con il numero 78,9563245. La arrotondiamo al decimo, al centesimo e al millesimo. Proviamo

Per cominciare, scartiamo l'intera parte. Otteniamo 0,9563245. Continueremo a lavorare con voi con questo particolare numero. Iniziamo a arrotondare con i millesimi, aumentando gradualmente la precisione.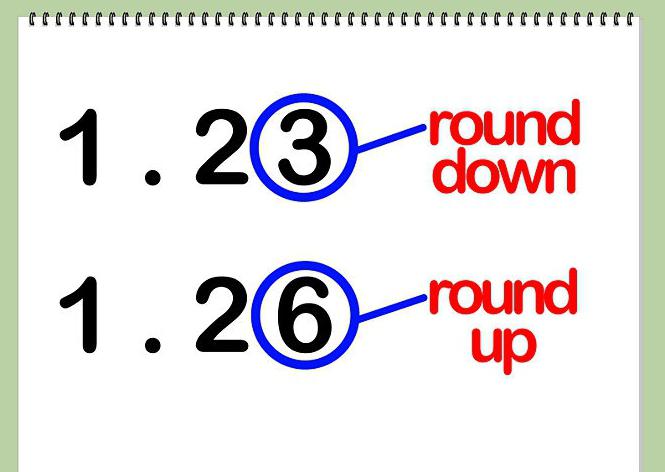

Il numero è 0.9563245. Verso zero. Il primo numero dalla fine è 5. Ciò significa che lo "convertiamo" in 0 e aggiungiamo 4 a 4. La seconda cifra - 4 + 1 = 5. Quindi assegniamo un'unità al segno successivo, e questo viene convertito in 0.

Finora abbiamo lavorato con te: 0.95632 ⁽⁺¹⁾ . L'arrotondamento alla millesima è di 3 cifre. Continuiamo a lavorare con te. 2 + 1 = 3. Questa cifra è inferiore a 5 secondi. Quindi, basta sostituirlo con 0 e rimuovere. Il prossimo stadio è 3-ka. Nulla è aggiunto ad esso. Basta sostituire con 0, poiché è inferiore a 5. L'abbiamo fatto con te: 0.956. Ora puoi aggiungere l'intera parte: 78.956.

Ma il nostro arrotondamento delle frazioni decimali non finisce qui. Ora dovresti tenerlo al centesimo. Per fare ciò, come prima, guardiamo l'ultima cifra dopo la virgola - 6. Secondo la regola, la sostituiamo con 0, quindi aggiungiamo semplicemente 1 alla cifra alla sua sinistra. Otteniamo 78.96. Arrotondare fino a decimi qui non è molto adatto. Riceviamo un intero con te. Dopo tutto, 6-ka sarà rimpiazzato da 0, l'unità sarà aggiunta a 9, e alla fine otterremo: 78,9 ⁽⁺¹⁾ . Risulterà 79. Questo è tutto. Ora sai come arrotondare le frazioni.