Esempio dell'algoritmo Diffie Hellman
La divulgazione dell'argomento della crittografia a chiave pubblica deve iniziare con il percorso storico del problema. Whitfield Diffie e Martin Hellman sono stati i primi a chiedere del metodo aperto di consegna delle chiavi. È successo nel 1976. La pubblicazione ha fatto i primi tentativi per affrontare il problema. La loro soluzione non era priva di difetti, ma gettava le basi per un modo completamente diverso di pensare nel campo della trasmissione dei dati crittografati.
Prerequisiti per la creazione di un algoritmo Diffie-Hellman
Fino a questo punto, l'autenticazione e la crittografia erano possibili solo attraverso una chiave segreta condivisa. Con lo sviluppo della tecnologia, la questione è diventata più acuta. Se 10 persone hanno bisogno di trasferire dati tra loro su canali non sicuri, dovranno scambiarsi le password l'una con l'altra. Questo compito sembra abbastanza reale. Anche con la necessità di aggiornarli. Dopotutto, per 10 amici occorrono solo 45 chiavi segrete. E se i contatti saranno 100? Ci vorranno 4950 password. La situazione sta crescendo come una palla di neve.
Ad
Il principale risultato di Diffie e Hellman era la corretta formulazione della domanda e la risposta ingegnosa ad essa. Hanno suggerito che i dati potevano essere crittografati in un modo e decrittografati in un altro. Cioè, hai 2 chiavi. Quello usato per la crittografia può essere lasciato aperto. Pertanto, chiunque può crittografare un messaggio, ma solo i proprietari della seconda chiave segreta possono decrittografarlo. Ma come implementare l'algoritmo per il trasferimento di tale chiave? Gli scienziati sono stati in grado di parzialmente e di dare una risposta.
Breve matematica: gruppi
L'algoritmo o protocollo Diffie-Hellman (ulteriore DH) funziona con l'aiuto dei numeri primi. Sia un numero abbastanza grande appartenente al set numeri primi L'algoritmo prevede l'utilizzo di un numero di 250-500 byte. Sia Za il gruppo moltiplicativo del modulo residuo a, che sarà usato dall'algoritmo di crittografia Diffie-Hellman. Consiste in un insieme di numeri 1, ..., a-1.
Ad
Prendi un elemento b dal gruppo Z a e considera una sequenza infinita 1, b, b 2 , b 3 , b 4 , ... Dal fatto che il gruppo Z a è per definizione un insieme finito, prima o poi la sequenza considerata {b} inizierà a ripetere. Impostare b i = b j (i <j).
Ora dividiamo ogni parte dell'uguaglianza di b i (modulo a) e prendiamo b ji = 1. Ciò significa che esiste un numero k = ji per il quale b k = 1 (mod a) è vero. Il k più piccolo per il quale questa uguaglianza regge è chiamato l'ordine di b. Per evitare confusione con altre pubblicazioni speciali, viene utilizzata la notazione matematica standard per spiegare il sistema Diffie-Hellman.
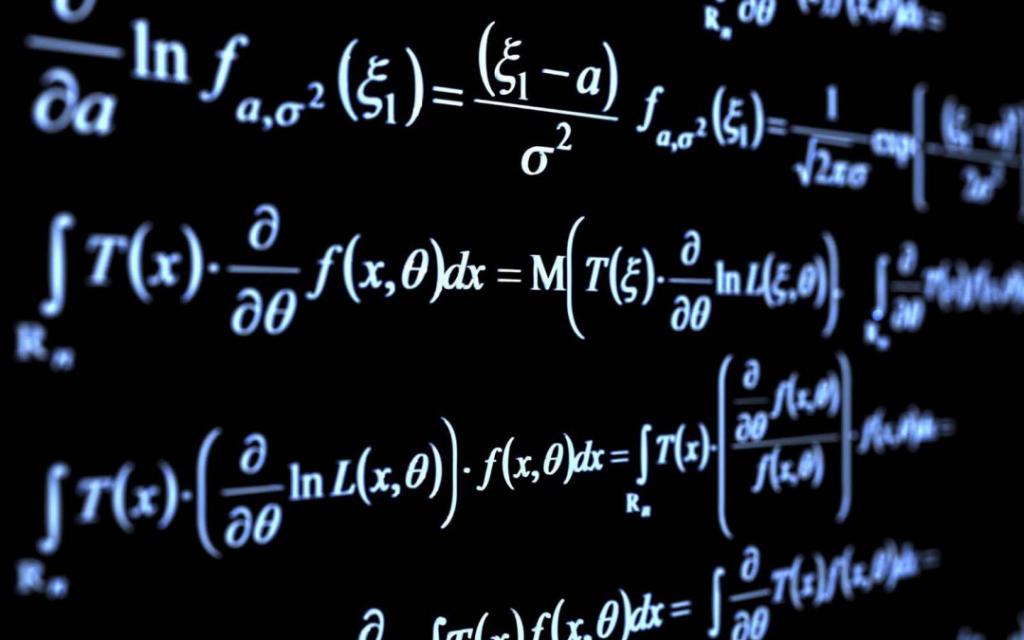
Quindi, elevando il numero b, chiamato l'elemento generatore, alla potenza, otteniamo una sequenza di numeri (set) 1, ..., b k-1 . Il numero di elementi in questo set è esattamente k.
La proprietà di moltiplicazione modulo a dice che esiste almeno un numero b che genera tutti gli elementi del gruppo Z * a . In altre parole, esiste un numero per cui k = a - 1 è vero. Questa proprietà ci consente di rappresentare i numeri del gruppo Z * a nella forma 1, b, b 2 , ... b a-2 . Tale numero b è chiamato un numero primitivo di un gruppo.
Ad
Nel sequel, è facile dimostrare dai segni di gruppo che l'insieme generato dal numero b è anche un gruppo stesso e eredita tutte le proprietà dei gruppi. In altre parole, le operazioni all'interno di un gruppo o sottogruppo generato possono essere eseguite esattamente nello stesso modo di un gruppo modulo a.
Considera la dichiarazione. Per ogni elemento b, il suo ordine è un divisore di a-1. È facile da mostrare Lascia a = 7. Il numero b = 3 è primitivo, poiché 1, ..., b 5 = 1, 3, 2, 6, 4, 5. Quindi il numero h = 2 genererà il sottogruppo 1, ..., h 2 = 1 , 2, 4, poiché h 3 = 2 3 mod 7 = 1. h = 6 genera il sottogruppo 1, 6. Le dimensioni dei gruppi sono 3 e 2, rispettivamente. Ovviamente, sono divisori del numero a-1 = 6.
Primo algoritmo DH
Nella versione originale, l'algoritmo ha funzionato come segue. Un grande numero a viene selezionato dall'insieme di elementi semplici e primitivi b generando Z * a . Entrambi i numeri aeb rappresentano la chiave pubblica, sono noti a tutti, compresi gli attaccanti. Come, quindi, nascondere i messaggi?
Fu a questo punto che Diffie e Hellman inventarono una mossa molto geniale. Supponiamo di avere due persone che comunicano tra loro: A e B. Primo, A sceglie un numero casuale x da Z * a , che equivale a scegliere un numero da {1, ..., a-1}. Quindi calcola il valore utilizzando la formula (b x mod a) e lo invia a B. A sua volta, B sceglie un certo numero y dallo stesso set, calcola il valore (b y mod a) e restituisce il risultato a A.
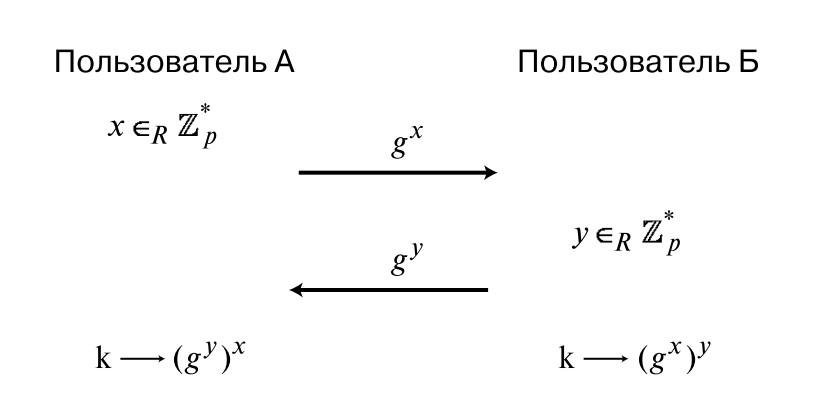
In un modo così complesso, risulta che la chiave segreta assomiglia a b xy . A causa della proprietà dei gradi, che dice g xy = (g y ) x , l'interlocutore A può calcolare il valore desiderato e decifrare le informazioni inviate a lui. Allo stesso modo, questo valore viene calcolato dall'interlocutore B. Pertanto, entrambi hanno la stessa chiave segreta.
Quali problemi incontra un intruso con questo scambio di informazioni? Può intercettare i numeri g x e g y . E anche con la conoscenza delle chiavi pubbliche, il problema del calcolo di g xy non è banale, t. Poiché non esiste un algoritmo efficace per trovare il valore desiderato nella distribuzione delle chiavi Diffie-Hellman. Questo problema è noto come problema di calcolo del logaritmo discreto.
Ad
Attacco mediatore
Uno dei punti deboli dell'algoritmo Diffie-Hellman primario è la sua vulnerabilità contro gli attacchi intermedi. Cosa significa? L'interlocutore A sa che comunica con un certo viso, ma in particolare con chi - non ne ha idea. Pertanto, l'attaccante può penetrare nel trasferimento di informazioni e imitare l'interlocutore B quando comunica con A, e viceversa. Nessuno di loro sarà in grado di sospettare che qualcosa non andasse.
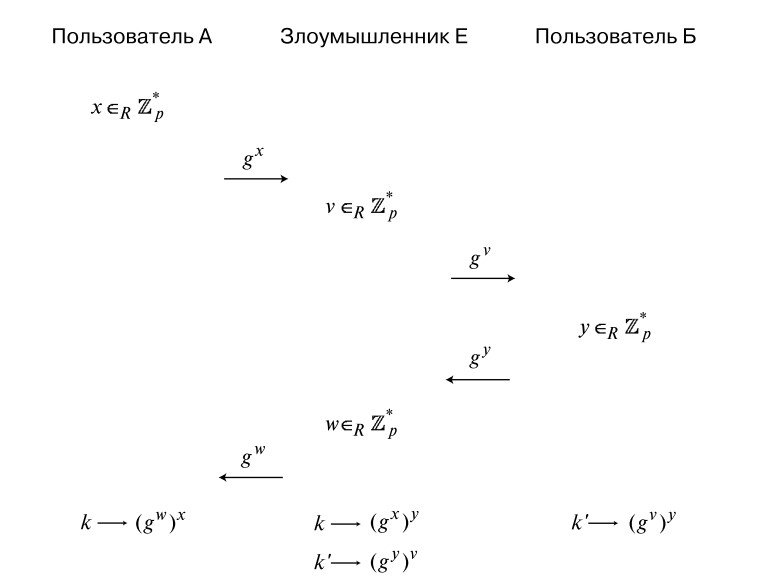
Esiste solo un'area di utilizzo in cui sono esclusi gli attacchi sull'algoritmo Diffie-Hellman. Questa è una telefonata e videochiamata. Qui gli interlocutori sono in grado di conoscersi, quindi il mediatore non sarà in grado di penetrare.
insidie
Oltre all'attacco mediatore, il protocollo DH ospita una miriade di altri problemi. Ad esempio, uno degli svantaggi è il caso in cui il primitivo non è un primitivo. Quindi genera solo un sottogruppo. A causa del restringimento del numero di opzioni possibili, l'attaccante apre la possibilità della loro ricerca.
Ad

I problemi dovuti a questa mancanza possono essere evitati se ciascuno degli interlocutori controlla che i numeri aeb siano corretti prima di iniziare lo scambio di dati. Cioè, a è un numero primo e b è un primitivo. Tuttavia, quando si tratta di sicurezza attraverso l'implementazione di alcuni passaggi uniformi e facoltativi, gli utenti spesso li ignorano.
Un altro serio problema sorge sulla base dei sottogruppi modulo a. Se l'attaccante sceglie di cambiare g x a 1 per rendere più facile per lui origliare, gli utenti possono facilmente rilevarlo controllando il numero per una corrispondenza. Tuttavia, se sostituisce la chiave con un numero di ordine basso, gli utenti non saranno in grado di sospettare nulla. E poiché il numero di elementi nell'insieme con un ordine basso sarà piccolo, l'attaccante dovrà selezionare un piccolo numero di opzioni per la decodifica.
Affidabilità dei numeri primi
L'algoritmo DH utilizza un numero ampio e affidabile di molti semplici. Come esattamente sceglierlo? Analizziamo i passaggi.
- Usando la formula a = 2k + 1, scegli i numeri a e k tali che siano semplici.
- Dall'insieme 1, ..., a-1, esclude 1 e a-1.
- Prendi un numero casuale x dal set rimanente dopo il secondo passo e trova il valore b = x 2 (mod a).
- Assicurati che b non sia uguale a 1 o a-1. Se b è uguale a uno dei valori proibiti, dovresti scegliere un'altra x. E ripeti l'operazione.
L'insieme (a, k, b) ottenuto in questo modo può essere considerato sufficiente per l'uso nell'algoritmo di scambio di chiavi Diffie-Hellman. Di conseguenza, il destinatario del messaggio deve anche controllare il valore, che deve essere una potenza di b, e assicurarsi (ad esempio, una funzione del simbolo di Legendre) che rientra nel set generato dal numero b.
Utilizzando sottogruppi
Lo svantaggio principale dell'algoritmo di cui sopra è l'efficienza insufficiente. Supponendo che la lunghezza del numero primo a sia n bit, allora k è n-1 bit. Si scopre che tutti i gradi saranno lunghi n-1. Quindi operazione elevamento a potenza in media consisterà di 3n / 2 moltiplicazioni mod a. Questo è un bel processo.

Per far fronte a questo problema, è stato deciso di utilizzare sottogruppi più piccoli. Qual è il guadagno in termini di prestazioni in questo caso? Se il numero a è composto da 2000 bit, sono necessarie 3000 operazioni di moltiplicazione per calcolare b x . Attraverso l'uso di sottogruppi, questo numero può essere ridotto a ~ 400. Questo significativo aumento dell'efficienza dell'algoritmo rende possibile la sua piena applicazione. Ad esempio, l'algoritmo Diffie-Hellman con tre o più membri.
Quale dovrebbe essere la lunghezza di a
La corretta selezione delle dimensioni dei parametri dell'algoritmo Diffie-Hellman è un'operazione piuttosto complicata. Un requisito comune nel mondo della crittografia è, ad esempio, la condizione che un utente malintenzionato abbia bisogno di almeno 2,128 passaggi per entrare nel sistema. Se negli algoritmi di crittografia simmetrica rispettare tale requisito è abbastanza semplice, negli algoritmi a chiave pubblica questo è un problema reale. Se si soddisfa il requisito di cui sopra, la lunghezza a deve essere composta da almeno 850 byte.

In pratica, questa dimensione crea grossi problemi di prestazioni nel sistema, poiché le operazioni con le chiavi pubbliche richiedono molto più tempo rispetto, ad esempio, alla crittografia simmetrica con chiavi a 128 o 256 bit. Allora come essere? La lunghezza minima di una chiave pubblica deve iniziare a 2048 bit. Sebbene più lunga è la chiave, maggiore è il livello di sicurezza. Occorre prendere in considerazione in primo luogo le prestazioni del sistema e il suo costo. Se ti permette di usare una chiave di 4096 bit, devi farlo.
Come viene valutato il livello di sicurezza richiesto?
Le dimensioni delle chiavi nella crittografia simmetrica rimangono invariate (128, 256 bit) per l'intera vita del sistema, mentre le dimensioni della chiave pubblica sono sempre un valore variabile. Se devi sviluppare un sistema che deve essere utilizzato per 30 anni e mantenere i dati segreti per almeno 20 anni dopo che il sistema è stato messo fuori uso, allora le dimensioni della chiave di crittografia simmetrica devono inizialmente essere sufficientemente grandi da proteggere il sistema per i prossimi 50 anni.
A causa di evidenti problemi di prestazioni, a causa del fatto che l'algoritmo Diffie-Hellman crittografa molte più operazioni, i requisiti per le chiavi pubbliche sono diversi. Rimane valido per un anno e protegge i dati per i prossimi 20 anni, ovvero, vengono utilizzati 21 anni. A causa delle sue dimensioni variabili, la chiave può essere cambiata ogni anno e creata sempre più a lungo per garantire il livello di sicurezza richiesto.
Ad esempio, le migliori stime mostrano che una chiave con una lunghezza di 256 byte è in grado di fornire protezione dati per ~ 20 anni, una lunghezza di 384 byte è 35 anni e con una lunghezza di 512 byte è 47 anni, ecc. Il numero è 6800 bit, assicurando che un utente malintenzionato Sono necessari 2.128 passaggi per craccarlo, derivati da stime simili. Tuttavia, questa è solo una previsione, di cui devi fidarti con grande cura. Puoi prevedere in modo abbastanza preciso lo sviluppo degli eventi per 10 anni, ma a 50 anni - questo è fantastico.
Raccomandazioni pratiche
Ecco alcuni consigli pratici sull'utilizzo del protocollo DH. Scegli k come numero primo di 256 bit. Questo è il minimo che può fornire almeno un livello adeguato di sicurezza contro gli attacchi. Per a, scegli un numero che dovrebbe avere la forma Na + 1, dove N è un numero intero. Circa la dimensione del numero a è stato detto prima. Dopodiché, un numero casuale b viene selezionato e controllato per diverse condizioni. Innanzitutto, non può essere un'unità. In secondo luogo, b k = 1.
A sua volta, qualsiasi partecipante alla comunicazione dovrebbe essere convinto di quanto segue:
- a e k sono numeri primi, la lunghezza di k è 256 bit, la lunghezza di p è piuttosto grande.
- il numero k è il divisore di a-1.
- b non è uguale a 1 eb = 1.
Queste condizioni dovrebbero essere verificate anche con una fiducia incondizionata nella fonte.
conclusione
L'algoritmo DH è una soluzione ingegnosa per uno dei problemi gravi ed è ancora attivamente utilizzato in una forma modificata per i moderni requisiti di sicurezza in vari protocolli. L'algoritmo Diffie-Hellman, ad esempio, viene utilizzato in alcune parti dell'implementazione del protocollo IKE. Tuttavia, il suo uso dovrebbe essere metodico e attento a causa della presenza di problemi evidenti e di gravi insidie.