Discriminante: esempi di soluzioni. Come risolvere equazioni di secondo grado attraverso discriminanti

Equazioni quadrate appaiono spesso durante la soluzione di vari problemi di fisica e matematica. In questo articolo vedremo come risolvere queste uguaglianze in modo universale "attraverso discriminanti". Esempi di uso delle conoscenze acquisite sono anche indicati nell'articolo.

Di quali equazioni stiamo parlando?

La figura seguente mostra una formula in cui x è una variabile sconosciuta e i caratteri latini a, b, c sono alcuni numeri noti.

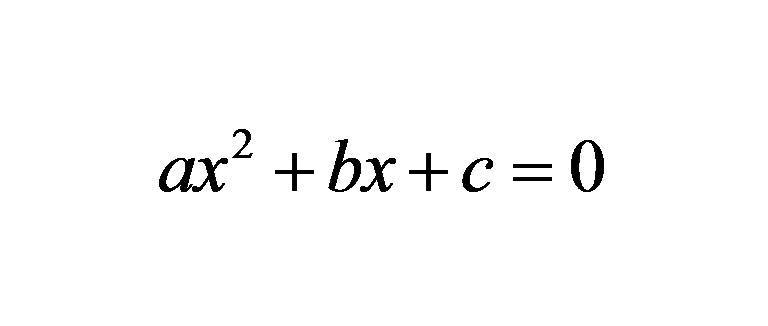
Ognuno di questi simboli è chiamato coefficiente. Come puoi vedere, il numero "a" si trova di fronte alla variabile x al quadrato. Questo è il massimo grado di espressione rappresentato, quindi è chiamato equazione quadratica. Il suo altro nome è spesso usato: equazione del secondo ordine. Il valore di un sé è un coefficiente quadrato (in piedi con una variabile al quadrato), b è un coefficiente lineare (è accanto a una variabile elevata alla prima potenza), e infine, il numero c è un termine libero.

Si noti che il tipo di equazione, che è mostrato nella figura sopra, è un'espressione quadrata classica comune. Oltre a ciò, ci sono altre equazioni del secondo ordine in cui i coefficienti b, c possono essere zero.

Quando il compito è risolvere l'uguaglianza considerata, ciò significa che tali valori della variabile x devono essere trovati in grado di soddisfarlo. Qui, la prima cosa da fare è ricordare la seguente cosa: poiché il massimo grado di X è 2, questo tipo di espressione non può avere più di 2 soluzioni. Ciò significa che se, mentre risolvendo l'equazione, sono stati trovati 2 valori di x che lo soddisfano, allora si può essere certi che non esiste un terzo numero, sostituendo invece che x, l'uguaglianza sarebbe anche vera. Le soluzioni di equazione in matematica lo chiamano radici.

Modi per risolvere le equazioni del secondo ordine

La soluzione di equazioni di questo tipo richiede la conoscenza di alcune teorie su di esse. In un corso di algebra scolastico vengono considerati 4 diversi metodi di soluzione. Li elenchiamo:

• usando la fattorizzazione;
• usando la formula per il quadrato completo;
• applicare il grafico della funzione quadratica corrispondente;
• usando l'equazione discriminante.

Inoltre, il primo metodo è la sua semplicità, tuttavia non può essere applicato a tutte le equazioni. Il secondo metodo è universale, ma piuttosto ingombrante. Il terzo metodo è notevole per la sua chiarezza, ma non è sempre conveniente e applicabile. E infine, l'uso dell'equazione discriminante è un modo universale e abbastanza semplice per trovare le radici di qualsiasi equazione di secondo ordine. Pertanto, nell'articolo consideriamo solo questo.

La formula per ottenere le radici dell'equazione

Passiamo alla forma generale di un'equazione quadratica. Lo scriviamo: a * x² + b * x + c = 0. Prima di usare il metodo per risolverlo "attraverso il discriminante", è necessario ridurre l'uguaglianza sempre alla forma registrata. Cioè, deve consistere di tre termini (o meno se b o c è 0).

Per esempio, se c'è un'espressione: x²-9 * x + 8 = -5 * x + 7 * x², allora dovresti prima trasferire tutti i suoi membri sullo stesso lato dell'equazione e aggiungere i termini contenenti la variabile x in uguali poteri.

In questo caso, questa operazione genererà la seguente espressione: -6 * x²-4 * x + 8 = 0, che equivale all'equazione 6 * x² + 4 * x-8 = 0 (qui abbiamo moltiplicato i lati sinistro e destro dell'uguaglianza di -1) .

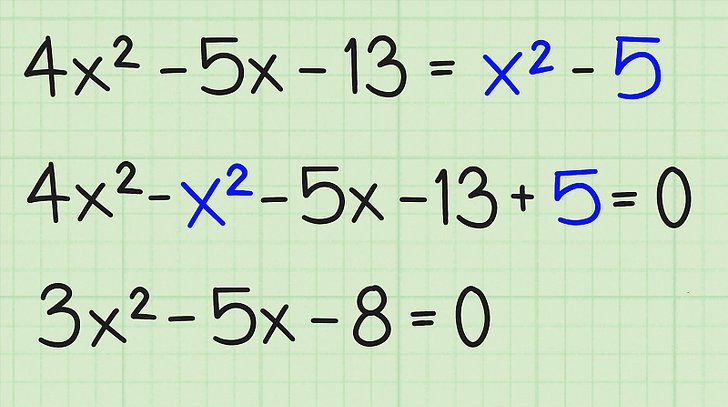
Una volta appreso il passo precedente, dovresti imparare a distinguere i coefficienti. Tutto è semplice qui: quando x² è sempre a, quando x ¹ è b, il termine libero c è un numero che non è correlato a x.

Nell'esempio sopra, a = 6, b = 4, c = -8. Si noti che tutti i membri dell'uguaglianza in considerazione vengono sempre sommati tra loro, quindi se appare il segno "-", significa che il coefficiente corrispondente è negativo, come c in questo caso.

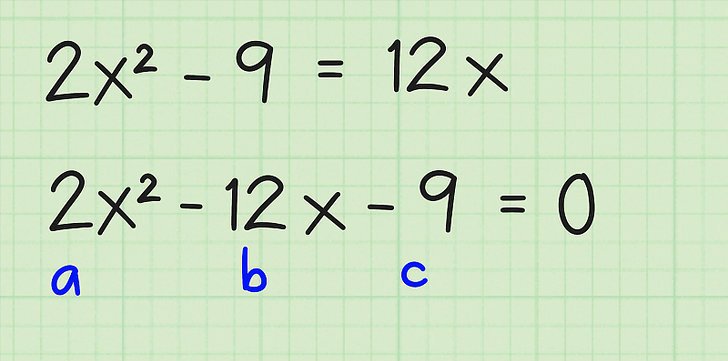
Dopo aver analizzato questo momento, passiamo ora alla formula stessa, che consente di ottenere le radici di un'equazione quadratica. Sembra che sia mostrato nella foto qui sotto.

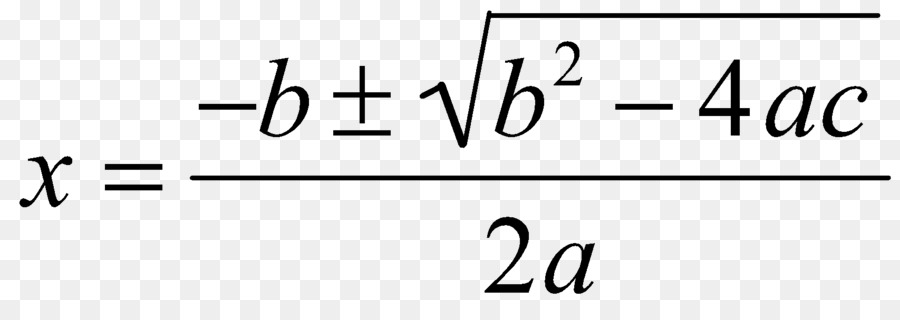
Come si può vedere da questa espressione, ti permette di ottenere due radici (dovresti prestare attenzione al segno "±"). Per fare ciò, è sufficiente sostituire i coefficienti b, c e a.

Concetto di discriminante

Nel paragrafo precedente è stata fornita una formula che consente di risolvere rapidamente qualsiasi equazione del secondo ordine. In esso, l'espressione radice è chiamata discriminante, ovvero D = b²-4 * a * c.

Perché questa parte della formula è isolata e ha persino il suo nome? Il fatto è che il discriminante collega tutti e tre i coefficienti dell'equazione in un'unica espressione. Quest'ultimo fatto significa che porta completamente informazioni sulle radici, che possono essere espresse nel seguente elenco:

1. D> 0: l'uguaglianza ha 2 soluzioni diverse, che sono entrambi numeri reali.
2. D <0: si ottengono anche due radici, ma entrambe sono complesse. Questo tipo di espressione è stato imparato a risolvere solo nel Rinascimento, quando la nozione di "unità immaginaria" è stata introdotta dai matematici del nuovo tempo.
3. D = 0: l'equazione ha solo una radice ed è un numero reale.

L'articolo fornisce inoltre esempi di equazioni quadratiche discriminanti e la loro soluzione.

Il compito di determinare il discriminante

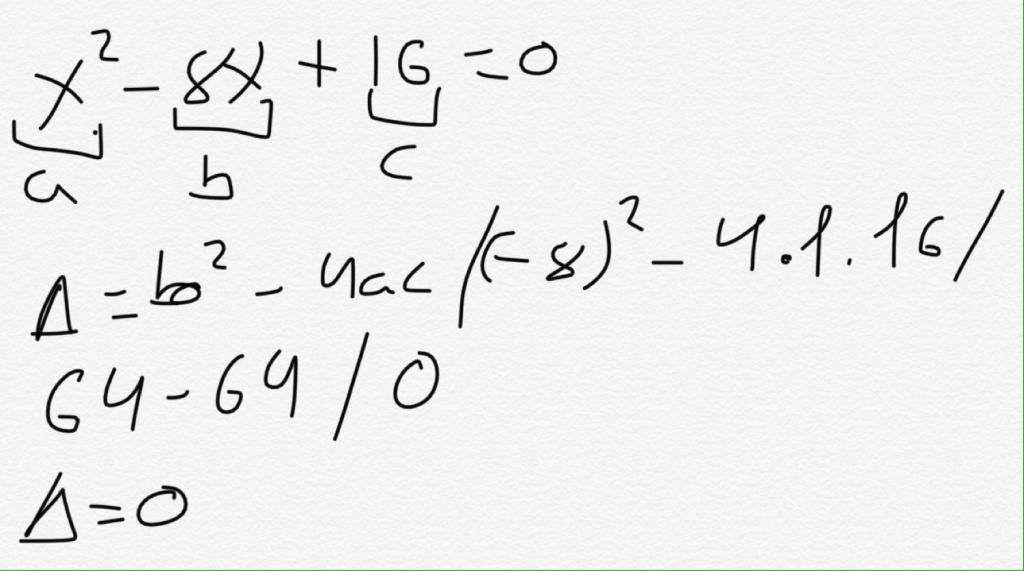
Diamo un semplice esempio di come trovare un discriminante. Sia data la seguente uguaglianza: 2 * x² - 4 + 5 * x-9 * x² = 3 * x-5 * x² + 7.

Lo portiamo al modulo standard, otteniamo: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) = 0, da dove arriviamo all'uguaglianza: -2 * x² + 2 * x-11 = 0. Qui a = -2, b = 2, c = -11.

Ora puoi usare la formula per il discriminante: D = 2² - 4 * (- 2) * (- 11) = -84. Il numero risultante è la risposta al compito. Poiché nell'esempio il discriminante è inferiore a zero, possiamo dire che questa equazione quadratica non ha radici reali. La sua decisione sarà solo i numeri del tipo complesso.

Un esempio di disuguaglianza attraverso il discriminante

Risolviamo problemi di un tipo leggermente diverso: l'uguaglianza data è -3 * x²-6 * x + c = 0. È necessario trovare i valori c per i quali D> 0.

In questo caso, sono noti solo 2 dei 3 coefficienti, quindi il valore esatto della discriminante non può essere calcolato, ma è noto che è positivo. Quest'ultimo fatto viene utilizzato nella costruzione della disuguaglianza: D = (-6) ²-4 * (- 3) * c> 0 => 36 + 12 * c> 0. La soluzione della diseguaglianza risultante porta al risultato: c> -3.

Controlla il numero risultante. Per fare ciò, calcoliamo D per 2 casi: c = -2 ec = -4. Il numero -2 soddisfa il risultato ottenuto (-2> -3), il discriminante corrispondente avrà il valore: D = 12> 0. A sua volta, il numero -4 non soddisfa la disuguaglianza (-4 <-3), calcoliamo il discriminante: D = -12 <0, che contraddice la condizione del problema.

Pertanto, qualsiasi numero c maggiore di -3 soddisferà la condizione.

Un esempio di risoluzione di un'equazione

Presentiamo il problema, che consiste non solo nel trovare il discriminante, ma anche nel risolvere l'equazione. È necessario trovare le radici per l'uguaglianza -2 * x² + 7-9 * x = 0.

In questo esempio, il discriminante è uguale al seguente valore: D = 81-4 * (- 2) * 7 = 137. Quindi le radici dell'equazione sono definite come: x = (9 ± √137) / (- 4). Questi sono i valori esatti delle radici, se calcoliamo approssimativamente la radice, allora otteniamo i numeri: x = -5.176 e x = 0.676.

Problema geometrico

Risolveremo un problema che richiederà non solo la capacità di calcolare il discriminante, ma anche l'applicazione delle abilità del pensiero astratto e della conoscenza, come creare equazioni di secondo grado.

Bob aveva un piumone che copriva 5 x 4 metri. Il ragazzo voleva cucirgli intorno al perimetro di una striscia solida di tessuto stupendo. Quanto sarà spessa questa striscia se è noto che Bob ha 10 m² di tessuto.

Lascia che la striscia abbia uno spessore di x m, quindi l'area del tessuto lungo il lato lungo della coperta sarà (5 + 2 * x) * x, e poiché i lati lunghi sono 2, abbiamo: 2 * x * (5 + 2 * x). Sul lato corto, l'area del tessuto cucito sarà 4 * x, poiché questi lati sono 2, otteniamo il valore di 8 * x. Si noti che il valore di 2 * x è stato aggiunto al lato lungo, poiché la lunghezza della coperta è aumentata di questo numero. L'area totale del tessuto cucita sulla coperta è di 10 m². Pertanto, otteniamo l'uguaglianza: 2 * x * (5 + 2 * x) + 8 * x = 10 => 4 * x² + 18 * x-10 = 0.

Per questo esempio, il discriminante è: D = 18²-4 * 4 * (- 10) = 484. La sua radice è 22. Usando la formula, troviamo le radici desiderate: x = (-18 ± 22) / (2 * 4) = (- 5; 0,5). Ovviamente, delle due radici, solo il numero 0.5 è adatto per la condizione del problema.

Quindi, la striscia di tessuto che Bob cuce alla sua coperta sarà larga 50 cm.