Dinamica e cinematica del moto circolare: formule e soluzione di un problema tipico
La capacità di descrivere il movimento in un cerchio è importante per il calcolo delle caratteristiche tecniche degli alberi rotanti e degli ingranaggi. Questo tipo di movimento si trova anche nella vita quotidiana e nella natura, come la rotazione dei pianeti attorno al sole e gli skater durante le esibizioni nelle competizioni sportive. In questo articolo considereremo come dal punto di vista della fisica questo tipo di movimento possa essere descritto.
Dinamica di rotazione
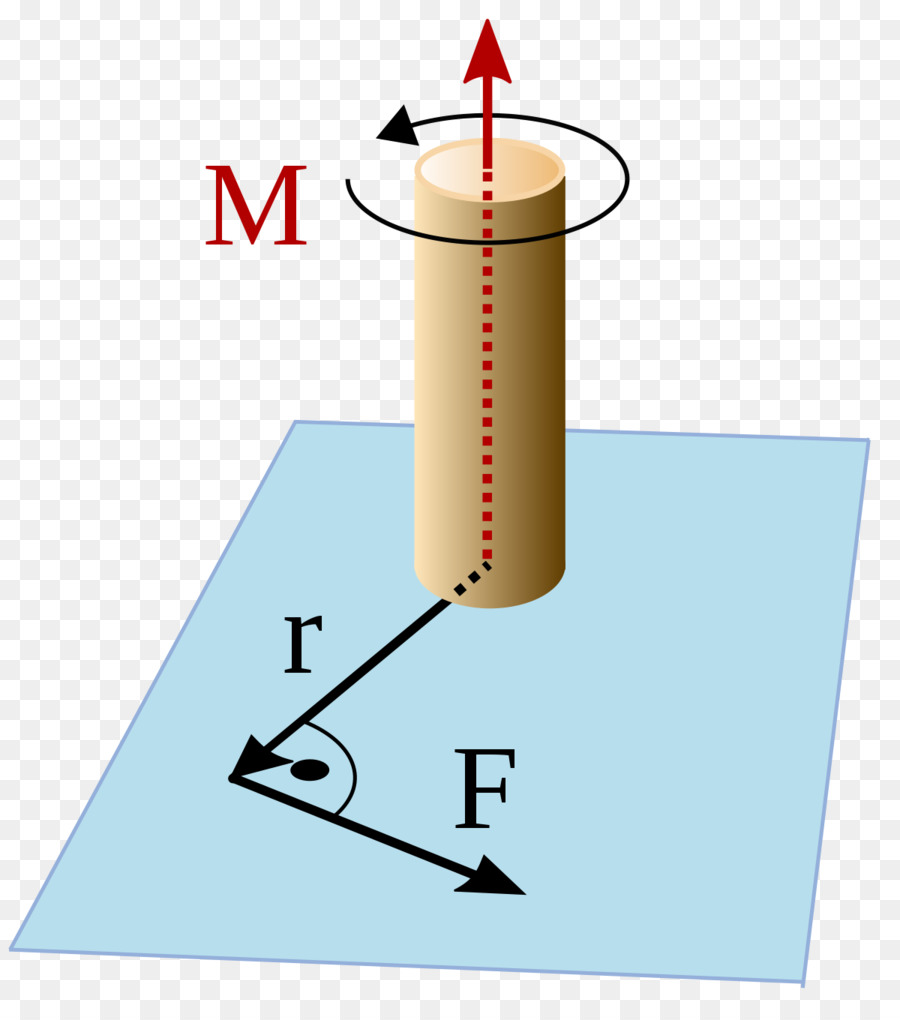
Il movimento in un cerchio è la rotazione di un certo corpo o di un punto materiale attorno ad un asse. Affinché il corpo inizi a ruotare, è necessario avere una coppia esterna che agisca sul sistema in questione. Questo momento è determinato dalla formula:
M = F * d
Qui F è la forza, d è la lunghezza della leva (la distanza tra l'asse e il punto di applicazione della forza). Il momento di forza è un valore vettoriale. La formula è utilizzata per calcolare il modulo M.
L'effetto del momento M si riflette sul sistema sotto forma di comparsa di accelerazione angolare. Cioè, il sistema inizia a ruotare. La formula principale per il movimento circolare è scritta come:
M = I * α
Qui sono il momento di inerzia, α è l'accelerazione angolare. Entrambe le quantità hanno i loro analoghi per il caso lineare. Se tutto è chiaro con l'analogo del valore α, allora per il momento di inerzia I è necessario chiarire. Il valore di I riflette le proprietà inerziali del sistema rotante. Cioè, durante la rotazione, ha lo stesso ruolo del normale peso corporeo.
Ad
Si noti che l'espressione di cui sopra è un analogo della seconda legge di Newton per la rotazione.
Forze centripete e centrifughe, accelerazione
Il processo di rotazione implica la presenza di una forza interna che assicurerebbe il movimento curvilineo del corpo. Questa forza è chiamata centripeta. Secondo il nome, è sempre diretto dal corpo all'asse di rotazione. Poiché la lunghezza della leva d per esso è zero, non conduce al verificarsi dell'accelerazione angolare α. Tuttavia, cambia il vettore di velocità lineare, cioè crea l'accelerazione.
L'accelerazione quando si muove in circolo senza cambiare il modulo della velocità lineare è detta centripeta. È calcolato dalla formula:
a c = v 2 / r
Dove v è la velocità lineare del punto materiale che ruota ad una distanza r dall'asse.
Oltre al centripeto, puoi sentire spesso parlare della forza centrifuga. Quest'ultimo cerca di portare il corpo da un percorso circolare a una linea retta. La ragione del suo verificarsi sono le proprietà inerziali del sistema rotante.
Ad
Quando si muove in un cerchio, le forze centripeta e centrifuga sono uguali in grandezza l'una rispetto all'altra e nella direzione opposta.
Equazioni di rotazione cinematiche
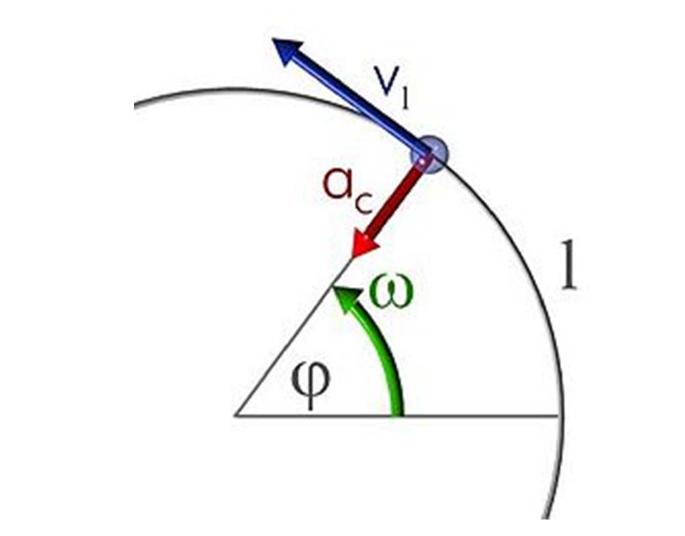
Il movimento in un cerchio, come in una linea retta, può essere uniforme o verificarsi con accelerazione. Nel primo caso, la formula è:
θ = ω * t
Cioè, l'angolo centrale θ, sul quale il corpo gira durante il tempo t, è direttamente proporzionale alla velocità angolare ω. L'angolo θ è espresso in radianti e la velocità ω è espressa in radianti al secondo.
Se un costante momento esterno di forze agisce sul sistema, allora il movimento in un cerchio avviene con una certa accelerazione costante α. In questo caso, la seguente espressione cinematica sarà vera:
Ad
θ = α * t 2/2
Se il sistema prima ruotava ad una certa velocità ω 0, e poi iniziava ad aumentare la sua frequenza di rotazione con l'accelerazione α, quindi, a partire dal momento del tempo t, quando appariva l'accelerazione, la formula sarà valida:
θ = ω 0 * t + α * t 2/2
Nota che questa espressione è una combinazione lineare di due precedenti.
La relazione delle caratteristiche cinematiche lineari e angolari
Sopra è stata data la formula per l'accelerazione centripeta, scritta attraverso la velocità lineare v. Tuttavia, questa formula può anche essere scritta in termini della corrispondente caratteristica angolare ω.
Supponiamo che un corpo rotante abbia fatto una rivoluzione attorno al cerchio nel tempo t. Quindi per velocità lineare e angolare possiamo scrivere:
v = 2 * pi * r / t;
ω = 2 * pi / t
Da ciò si vede che il modulo della velocità lineare v è r volte la grandezza della grandezza di ω, cioè:
v = ω * r
Questa uguaglianza collega velocità angolari e lineari. Usandolo, puoi scrivere la formula per un c attraverso ω:
a c = ω 2 * r
Ora calcoliamo nella formula con le velocità la derivata temporale per i lati sinistro e destro dell'uguaglianza, otteniamo:
dv / dt = dω / dt * r =>
a = α * r
Questa uguaglianza collega l'accelerazione lineare a diretta tangenzialmente al cerchio e il suo analogo angolare α.
È facile dimostrare che l'angolo di rotazione centrale θ quando si muove attorno a un cerchio è correlato alla lunghezza del suo arco L, la seguente espressione:
L = θ * r
Qui, se θ è uguale a 2 * pi radianti (giro completo), otteniamo la lunghezza del cerchio L.
La soluzione al problema di determinare la forza centripeta
È noto che una pietra del peso di 0,5 kg è stata legata a una fune lunga 1 metro e hanno iniziato a ruotarla con una frequenza angolare di 3 giri al secondo. È necessario trovare la forza di tensione della fune F c .
Ad
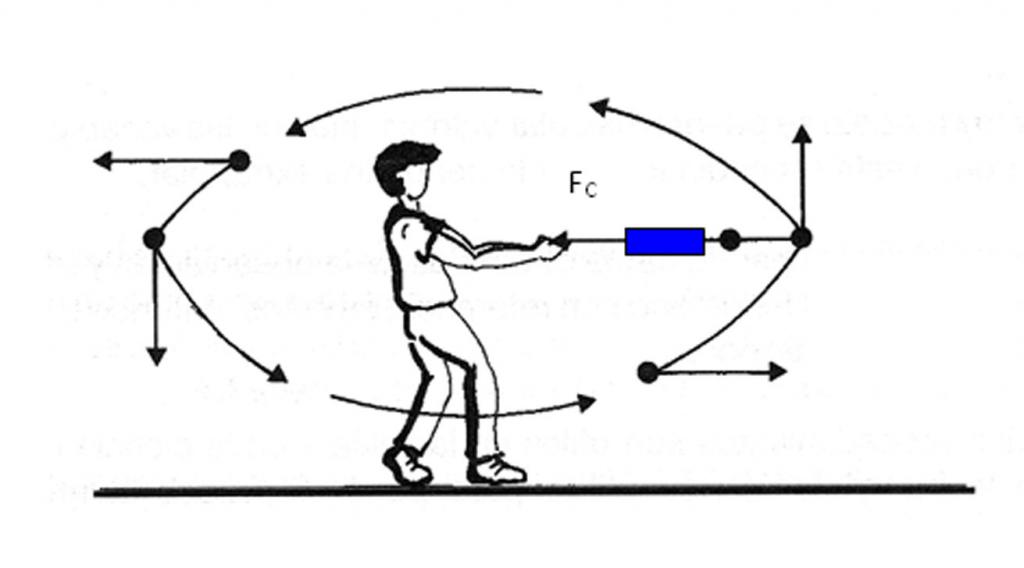
La forza di tensione F c è centripeta. Può essere calcolato con la formula:
F c = m * a c
La massa di pietra m è conosciuta. L'accelerazione centripeta a c può essere calcolata dalla conoscenza della velocità angolare ω. Con la frequenza f impostata nell'attività, la quantità ω è correlata all'espressione:
ω = 2 * pi * f
Quindi l'accelerazione centripeta sarà calcolata come:
a c = 4 * pi 2 * f 2 * r
La forza desiderata F c sarà uguale a:
F c = 4 * pi 2 * f 2 * r * m
Se la condizione del problema è sostituire i dati in questa formula, otteniamo il valore della forza F c , approssimativamente uguale a 177.5 N.