Condizione di equilibrio della leva. La regola dei momenti. Meccanismi semplici. Compiti e soluzioni
Da tempo immemorabile, l'umanità ha utilizzato vari meccanismi progettati per facilitare il lavoro fisico. Uno di questi è una leva. Che cos'è, qual è l'idea del suo utilizzo e qual è la condizione di equilibrio della leva, questo articolo è dedicato alla considerazione di tutti questi problemi.
Quando l'umanità ha iniziato ad applicare il principio della leva finanziaria?

È difficile rispondere a questa domanda con precisione, poiché i meccanismi semplici erano già noti agli antichi egizi e agli abitanti della Mesopotamia fin dal tremila anni prima di Cristo.
Uno di questi meccanismi è la cosiddetta leva gru. Rappresentava un lungo palo, che si trovava sul supporto. Quest'ultimo è stato installato più vicino a un'estremità del palo. Verso la fine, che era più lontano dal punto di riferimento, hanno legato una nave, dall'altra hanno messo un contrappeso, ad esempio una pietra. Il sistema è stato regolato in modo tale che una nave riempita a metà conducesse alla posizione orizzontale del palo.
Ad
La gru a leva serviva a sollevare l'acqua da un pozzo, da un fiume o da altra depressione fino al livello in cui si trovava la persona. Applicando una piccola forza alla nave, la persona la abbassò alla fonte d'acqua, la nave fu riempita di liquido, e quindi, applicando una piccola forza all'altra estremità del polo con contrappeso, fu possibile sollevare la nave indicata.
La leggenda di Archimede e la nave
Tutti conoscono l'antico filosofo greco della città di Siracusa, Archimede, che nei suoi scritti non solo descrive il principio di funzionamento dei meccanismi semplici (leva, tavola inclinata), ma ha anche portato alle corrispondenti formule matematiche. Fino ad oggi, la sua frase rimane famosa:
Dammi un punto d'appoggio e sposterò questo mondo!

Come sai, nessuno gli ha dato un tale sostegno e la Terra è rimasta al suo posto. Tuttavia, ciò che Archimede era davvero in grado di spostare era la nave. Una delle leggende di Plutarco (l'opera "Parallel Lives") dice quanto segue: Archimede, in una lettera al suo amico, il re Ierone di Siracusa, disse che poteva solo spostare un peso arbitrariamente grande, a certe condizioni. Hieron fu sorpreso da una tale affermazione del filosofo e gli chiese di dimostrare di cosa stava parlando. Archimede fu d'accordo. In uno dei giorni, la nave di Hieron, sul molo, era carica di gente e barili riempiti d'acqua. Il filosofo, seduto a una certa distanza dalla nave, era in grado di sollevarlo sopra l'acqua, tirando le corde, mentre applicava un piccolo sforzo.
Componenti della leva
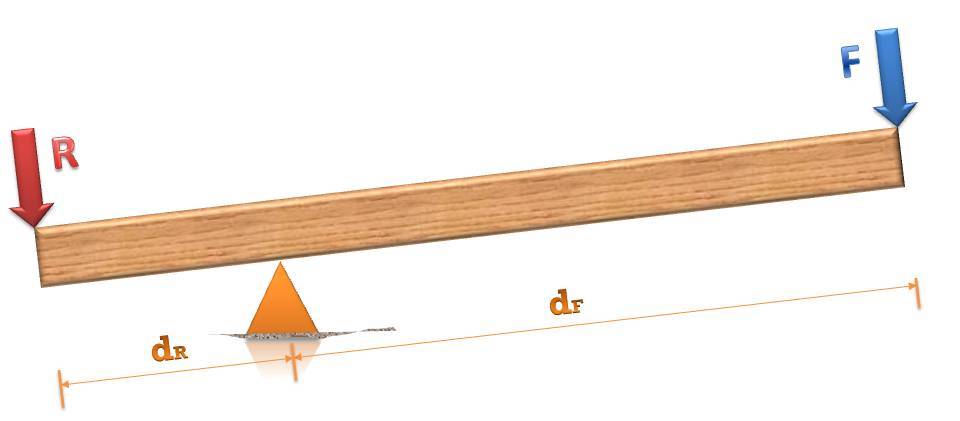
Nonostante il fatto che stiamo parlando di un meccanismo abbastanza semplice, ha ancora un certo dispositivo. Fisicamente, si compone di due parti principali: un palo o trave e un supporto. Quando si considerano gli stessi compiti, il polo viene considerato come un oggetto costituito da due (o uno) bracci. La spalla è una parte del polo, che è relativa al supporto su un lato. Un grande ruolo nel principio di funzionamento del meccanismo in esame è esattamente la lunghezza della spalla.
Quando si considera la leva nel lavoro, ci sono due ulteriori elementi: la forza applicata e il potere di contrastarlo. Il primo cerca di mettere in moto un oggetto che crea una forza di opposizione.
Ad
Condizione di equilibrio della leva in fisica
Conoscenza del dispositivo di questo meccanismo, presentiamo una formula matematica, con la quale possiamo dire quale braccio della leva si muoverà in quale direzione o, al contrario, l'intero dispositivo sarà a riposo. La formula ha la forma:
F 1 * l 1 = F 2 * l 2 ,
dove F 1 e F 2 sono le forze di azione e reazione, rispettivamente, l 1 e l 2 sono le lunghezze delle braccia a cui sono applicate queste forze.
Questa espressione consente di esplorare le condizioni di equilibrio di una leva avente un asse di rotazione. Quindi, se la spalla l 1 è maggiore di l 2 , per bilanciare la forza F 2 è necessario un valore inferiore F 1 . Al contrario, se l 2 > l 1 , quindi per contrastare la forza F 2 dovrai attaccare un grande F 1 . Queste conclusioni possono essere ottenute riscrivendo l'espressione sopra nella seguente forma:
Ad
F 1 / F 2 = l 2 / l 1 .
Come si può vedere, le forze coinvolte nel processo di formazione di un equilibrio sono inversamente correlate alla lunghezza dei bracci della leva.
Qual è il guadagno e la perdita quando si utilizza la leva?
Ne deriva una conclusione importante dalle formule di cui sopra: con l'aiuto di un braccio lungo e di un piccolo sforzo, è possibile spostare oggetti con una massa enorme. Questo è vero, e molti potrebbero pensare che l'uso di una leva porti ad un guadagno nel lavoro. Ma non lo è. Il lavoro è una quantità di energia che non può essere creata dal nulla.
Analizziamo il lavoro di una leva semplice con due reticolazione l 1 e l 2 . Supponiamo che alla fine della spalla l 2 esista un peso P (F 2 = P). Alla fine dell'altra spalla, la persona applica la forza F 1 e solleva questo carico all'altezza h. Ora, calcoliamo il lavoro di ciascuna forza e identifichiamo i risultati ottenuti. Otteniamo:
Ad
F 1 * x = F 2 * h.
La forza F 2 ha agito lungo una traiettoria verticale di lunghezza h, a sua volta F 1 ha agito anche lungo la verticale, ma era già collegata all'altro braccio, la cui estremità si muoveva di una quantità sconosciuta x. Per trovarlo, è necessario sostituire nell'ultima espressione la formula di collegamento tra le forze e le braccia della leva. Esprimendo x, abbiamo:
x = F 2 * h / F 1 = l 1 * h / l 2 .
Questa uguaglianza mostra se l 1 > l 2 , quindi F 2 > F 1 e x> h, cioè applicando una piccola forza, è possibile sollevare un carico con un peso elevato, ma è necessario spostare il braccio di leva corrispondente (l 1 ) su uno più grande. la distanza Al contrario, se l 1 <l 2 , quindi F 2 <F 1 e x <h, cioè il peso di un certo peso può essere aumentato ad un'altezza h h spostando la spalla l 1 ad un'ampiezza più piccola, ma devi applicare una forza sufficientemente grande F 1 . Nel primo caso, si ottiene il guadagno in potenza, nel secondo nel modo o nella velocità.
Pertanto, la leva non ha alcun beneficio nel lavoro, ma consente solo di ridistribuirla a favore di una forza applicata più piccola, o in favore di una maggiore ampiezza di movimento dell'oggetto. Un principio filosofico generale funziona nel campo della fisica in discussione: qualsiasi guadagno è compensato da una certa perdita.
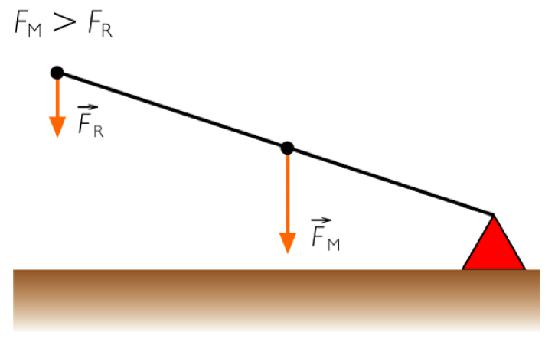
Tipi di leve
A seconda dei punti di applicazione della forza e della posizione del supporto, si distinguono i seguenti tipi di questo meccanismo:
- Il primo tipo: il fulcro è tra le due forze F 1 e F 2 , quindi, la lunghezza delle braccia determinerà ciò che dà un tale vantaggio. Un esempio sono le normali forbici.
- Il secondo tipo Qui la forza contro cui si sta facendo il lavoro si trova tra il supporto e la forza applicata. Questo tipo di costruzione significa che darà sempre un guadagno di forza e una perdita di marcia e velocità. Il suo esempio è una macchina da giardino.
- Il terzo tipo. L'ultima opzione, che resta da realizzare in questo semplice progetto, è la posizione della forza applicata tra il supporto e la forza di resistenza. In questo caso, il guadagno nel modo, ma la perdita è in vigore. Un esempio potrebbe essere una pinzetta.

Il concetto del momento di forza
La considerazione di eventuali problemi nella meccanica, che comprendono i concetti di asse o punto di articolazione, viene eseguita utilizzando la regola del momento di forza. Poiché il supporto della leva è anche l'asse (punto) attorno al quale ruota il sistema, il momento di forza viene anche utilizzato per stimare l'equilibrio di questo meccanismo. Con questo si intende una quantità in fisica, uguale al prodotto della spalla e della forza che agisce, cioè:
M = l * F.
Data questa definizione, la condizione di equilibrio della leva può essere riscritta come segue:
M 1 = M 2 , dove M 1 = l 1 * F 1 e M 2 = l 2 * F 2 .
Il momento M è additivo, il che significa che il totale momento di forza per il sistema in questione può essere ottenuto con la solita aggiunta di tutti i momenti in cui agisco su di esso. Tuttavia, si dovrebbe tener conto del loro segno (la forza che fa girare il sistema in senso antiorario crea un momento positivo + M, e viceversa). Detto questo, la regola dei momenti per una leva in equilibrio sarà simile a questa:
Ad
M 1 - M 2 = 0.
La leva perde il suo equilibrio quando M 1 ≠ M 2 .
Dove viene utilizzato il principio della leva?
Abbiamo già citato alcuni esempi dell'uso di questo meccanismo semplice e ben noto dai tempi antichi. Ecco alcuni esempi aggiuntivi:
- Pinze: una leva del primo tipo, che consente di creare enormi sforzi a causa della piccola lunghezza delle spalle l 2 in cui si trovano i denti dell'utensile.
- Apriscatole coperchi lattine e bottiglie: è una leva del 2 ° tipo, quindi dà sempre un guadagno nello sforzo.
- Canna da pesca: la leva del 3 ° tipo, che ti permette di spostare l'estremità della canna da pesca con un galleggiante, un piombino e un amo per ampiezze maggiori. La perdita in questo caso si fa sentire quando il pescatore trova difficile pescare fuori dall'acqua, anche se il suo peso non supera 0,5 kg.

L'uomo stesso con le sue articolazioni, i muscoli, le ossa e i tendini è un vivido esempio di un sistema con molte leve diverse.
Problem solving
La condizione di equilibrio della leva discussa nell'articolo viene utilizzata per risolvere un semplice problema. È necessario calcolare la lunghezza approssimativa del braccio della leva, applicando uno sforzo alla fine del quale, Archimede è stato in grado di sollevare la nave, come la descrive Plutarco.

Per risolvere, introduciamo le seguenti ipotesi: prendiamo in considerazione la trireme greca di 90 tonnellate con uno spostamento e assumiamo che il supporto della leva fosse a 1 metro dal suo centro di massa. Come Archimede, secondo la leggenda, potrebbe facilmente sollevare la nave, allora assumeremo che a questo scopo ha applicato una forza pari alla metà del suo peso, cioè circa 400 N (per una massa di 82 kg). Quindi, applicando la condizione di equilibrio della leva, otteniamo:
F 1 * l 1 = F 2 * l 2 => l 1 = F 2 * l 2 / F 1 = m * g * l 2 / F 1 = 90000 * 9,81 * 1/400 ≈ 2,2 km.
Anche se aumentiamo la forza applicata al valore del peso di Archimede stesso e portiamo il supporto altre due volte, allora la lunghezza della spalla sarà di circa 500 metri, che è anche un grande valore. Molto probabilmente, la leggenda di Plutarco è un'esagerazione per dimostrare l'efficacia della leva, e Archimede in realtà non ha sollevato la nave sopra l'acqua.