Trova la radice dell'equazione? È facile!
In matematica ci sono una varietà di equazioni. Hanno sempre bisogno di essere risolti, cioè di cercare tutti i numeri che lo renderanno una vera uguaglianza. I modi di trovare soluzioni sono determinati dalla forma originale dell'equazione. Da esso dipenderà dal numero di valori veri della variabile, che sono designati come la radice dell'equazione. Questo numero può variare da zero a infinito.
Cosa si intende per equazione e radice?
Dal titolo è chiaro che equivale a due valori che possono essere rappresentati da espressioni numeriche o alfabetiche. Inoltre, contengono quantità ancora sconosciute. L'equazione più semplice ha solo uno.
Esistono molti tipi di equazioni, ma il concetto di una radice è sempre lo stesso per loro. La radice di un'equazione è un valore di un numero sconosciuto a cui l'equazione assume una vera uguaglianza. Ci sono situazioni in cui ci sono molti di questi numeri, quindi lo sconosciuto è chiamato una variabile.
Ad
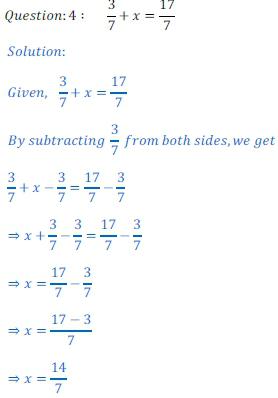
Trovare tutte le possibili radici di un'equazione è la sua soluzione. Cioè, è necessario eseguire una serie di operazioni matematiche che lo semplificano. E poi portare all'uguaglianza, che contiene solo l'ignoto e un numero.
In algebra, quando risolviamo le equazioni, si può arrivare alla situazione che non ci saranno radici. Quindi dicono che è insolubile. E nella risposta di tale equazione è necessario annotare che non ci sono soluzioni.
Ma a volte succede il contrario. Cioè, le radici estranee appaiono nel processo di numerose trasformazioni. Non daranno la vera uguaglianza alla sostituzione. Pertanto, i numeri dovrebbero sempre essere controllati per evitare la situazione con le radici non necessarie nella risposta. Altrimenti, l'equazione non sarà considerata risolta.
Ad
Informazioni sull'equazione lineare
Può sempre essere trasformato in un record della seguente forma: a * x + v = 0. In esso, "a" è sempre diverso da zero. Per capire quante radici ha un'equazione, dovrà essere risolta in una forma generale.
Trasformazioni dell'algoritmo:
- sposta il termine "in" sul lato destro dell'uguaglianza, sostituendo il suo segno con l'opposto;
- dividere entrambi i lati dell'uguaglianza risultante per il coefficiente "a".
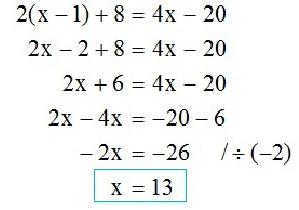
La visione generale della soluzione è:
x = -in / a .
È chiaro da ciò che la risposta è un numero. Questa è solo una radice.
Equazione quadratica
La sua forma generale: a * x 2 + b * x + c = 0 . Qui i coefficienti sono numeri qualsiasi tranne il primo, "a", che non può essere uguale a zero. Dopotutto, diventerà automaticamente lineare. La risposta alla domanda su quante radici ha l'equazione non è più così semplice come nel caso precedente.
Tutto dipenderà dal valore del discriminante. È calcolato dalla formula D = in 2 - 4 a * s . Dopo i calcoli, la "D" potrebbe risultare più, meno o uguale a zero. Nel primo caso, le radici dell'equazione saranno due, nel secondo la risposta sarà "senza radici" e la terza situazione darà solo un valore sconosciuto.
Formule utilizzate per trovare le radici di un'equazione quadratica e contenenti una discriminante
Nel caso generale, quando "D" è un numero positivo, diverso da zero, è necessario utilizzare la seguente formula:
Ad
х 1,2 = (-в ± √Д) / (2 * а) .
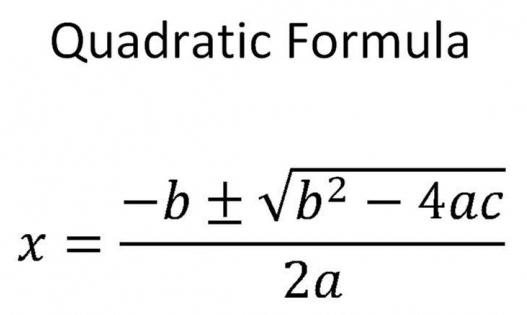
Ci sono sempre due risposte qui. Ciò è dovuto al fatto che la formula originale è un segno più / meno. Cambia significativamente il valore dell'ignoto.
Quando "D" è uguale a zero, la radice dell'equazione è l'unico numero. Solo perché radice quadrata da zero è zero. Quindi, aggiungere e sottrarre dovrà essere zero. Da questo numero non cambierà. Pertanto, la formula della radice dell'equazione può essere scritta senza menzionare "D":
x = (-v) / (2 * a).
Se il discriminante è negativo, non è possibile estrarre la radice quadrata da esso. Pertanto, le radici di tale equazione non saranno.
Nota. Questo è vero per un corso scolastico che non viene insegnato. numeri complessi. Quando vengono inseriti, si scopre che in questa situazione ci saranno due risposte.
Formule per il calcolo delle radici di un'equazione quadratica che non usano discriminante
Stiamo parlando del teorema di Viet. È valido nel caso in cui l'equazione quadratica è scritta in una forma leggermente diversa:
x 2 + c * x + c = 0.
Quindi la formula radice equazione quadratica si riduce a soddisfare la soluzione di due linee lineari:
x 1 + x 2 = -in
e
x 1 * x 2 = s.
È risolto a causa del fatto che l'espressione per una delle radici deriva dal primo. E questo valore deve essere sostituito nel secondo. Quindi verrà trovata la seconda radice e quindi la prima.
Questa opzione può sempre venire dalla forma generale di un'equazione quadratica.
È sufficiente dividere tutti i coefficienti in "a".
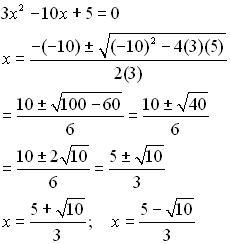
Cosa succede se è necessario conoscere il valore più piccolo della radice?
Risolvi l'equazione e trova tutti i numeri possibili adatti per la risposta. E poi scegli il più piccolo. Questa sarà la radice più piccola dell'equazione.
Ad
Molto spesso, tali domande si trovano in attività che hanno un grado maggiore di 2 o contengono funzioni trigonometriche. Un esempio di quando è necessario trovare la radice più piccola è la seguente uguaglianza:
2 x 5 + 2 x 4 - 3 x 3 - 3 x 2 + x + 1 = 0.
Per trovare ogni valore che può essere chiamato la "radice dell'equazione", questa equazione deve essere trasformata. La prima azione: raggruppare i suoi membri in coppie: la prima con la seconda e così via. Quindi da ogni coppia per fare un fattore comune.
In ogni parentesi rimarrà (x + 1). Il fattore comune nella prima coppia sarà 2 x 4 , nel secondo 3 x 2 . Ora di nuovo è necessario fare l'imposizione di un fattore comune, che sarà la stessa parentesi.
Dopo che il moltiplicatore (x + 1) sarà (2 x 4 - 3 x 2 + 1). Il prodotto di due fattori è uguale a zero, solo se uno di essi assume un valore uguale a zero.
La prima parentesi è zero per x = -1. Questa sarà una delle radici dell'equazione.
Altri saranno ottenuti dall'equazione formata dalla seconda parentesi, equiparata a zero. È biquadratico. Per risolverlo, devi inserire la notazione: x 2 = y. Quindi l'equazione cambierà in modo significativo e assumerà la forma normale di un'equazione quadratica.
La sua discriminante è D = 1. È maggiore di zero, il che significa che ci saranno due radici. La prima radice è uguale a 1, la seconda sarà 0.5. Ma questi sono i valori per y.
È necessario tornare alla designazione inserita. x 1.2 = ± 1, x 3.4 = ± √0.5. Tutte le radici dell'equazione: -1; 1; -√0,5; √0,5. Il più piccolo di questi è -1. Questa è la risposta.
In conclusione
Promemoria: tutte le equazioni devono essere controllate se la radice è appropriata. Forse è un estraneo? Vale la pena controllare l'esempio proposto.
Se sostituiamo l'unità nell'equazione inizialmente data invece di "x", allora risulta che 0 = 0. Questa radice è corretta.
Se x = -1, il risultato è lo stesso. Anche la radice è adatta.
Allo stesso modo, con i valori di "x" uguali a -√0.5 e √0.5, la vera uguaglianza esce ancora. Tutte le radici si adattano.
Questo esempio non ha fornito radici estranee. Questo non è sempre il caso. Potrebbe essere che il valore più piccolo non sia adatto per il test. Quindi dovrei scegliere dal resto.
Conclusione: è necessario ricordare il controllo e approcciare attentamente la soluzione.