Teoria dei grafi: definizioni di base

La teoria dei grafi è una branca della matematica usata in informatica e programmazione, economia, logistica e chimica.

Cos'è un grafico

Spesso, i sistemi grafici sono usati per descrivere la struttura dei sistemi. Gli elementi in essi sono rappresentati da cerchi, punti, quadrati, ecc. E le connessioni tra gli elementi sono linee o frecce. Allo stesso tempo, né il modo in cui gli elementi sono rappresentati, né la lunghezza o la forma delle linee è importante, ma solo quali elementi sono collegati. Quindi, un grafico è una coppia della forma (A, M), dove A è un insieme finito di vertici, e M è un insieme di spigoli - linee che collegano alcuni vertici.

Concetti di base della teoria dei grafi

Per un grafo o digramma diretto (vedi figura sotto), i bordi sono orientati, chiamati archi e sono rappresentati da frecce. Un arco può essere designato da una coppia ordinata di vertici che collega: iniziale e finale.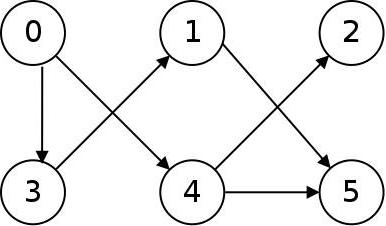

Per un grafico non orientato (vedere la figura seguente), i bordi sono rappresentati da linee senza orientamento. Di conseguenza, la coppia di vertici che il bordo si collega non è ordinata. Entrambi questi vertici sono le estremità di un bordo.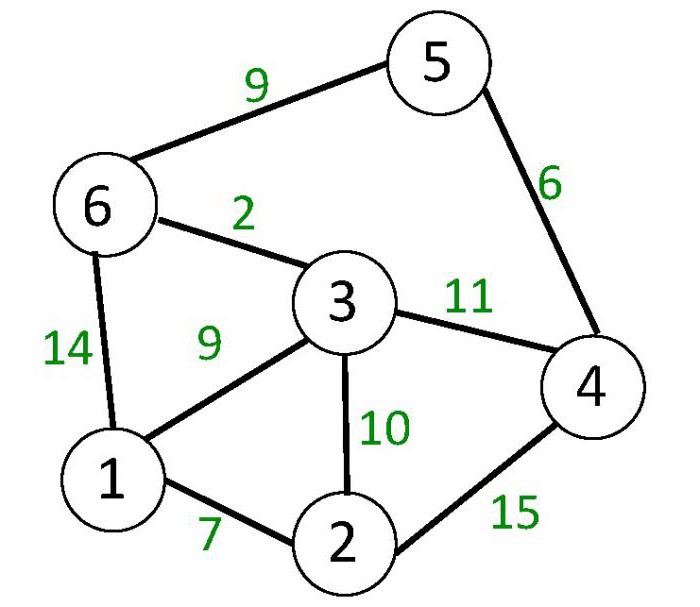

Se i vertici a e b sono le estremità di un bordo (o l'inizio e la fine di un arco) di un grafico, allora diciamo che i vertici aeb sono incidenti su questo bordo (arco), anche il bordo (arco) è incidente ai vertici a e b. Se i vertici a e b sono le estremità di un bordo, allora loro (aeb) sono chiamati adiacenti.

Spesso si considera che i grafici, i cui bordi sono dello stesso tipo, siano orientati o meno.

Se i bordi hanno lo stesso inizio e fine, vengono chiamati più spigoli e il grafico in cui sono presenti è chiamato multigrafo.

La teoria dei grafi usa anche il concetto di "loop" - un bordo che va e si pone sullo stesso vertice. Il grafico in cui ci sono i loop è chiamato pseudografo.

I grafici non orientati più comuni che non hanno bordi multipli e nessun loop. Tali grafici sono chiamati ordinari. Non hanno bordi multipli, quindi puoi identificare il bordo e la corrispondente coppia di vertici.

Ogni vertice del digramma è caratterizzato da:

• Mezza un risultato. Questo è il numero di archi che ne escono.
• Indegree. Questo è il numero di archi che vanno in un dato vertice.

La somma dei mezzi gradi di entrata del digramma, così come la somma dei semi-gradi del risultato, sono uguali al numero totale di archi del grafico.

In un grafo non orientato, ciascun vertice è caratterizzato dal grado del suo vertice. Questo è il numero di spigoli che si verificano in alto. La somma totale dei gradi dei vertici del grafico è il numero di lati moltiplicato per due: ciascun bordo darà un contributo uguale a due.

Un vertice con grado 0 è chiamato isolato.

Il picco sospeso è un vertice di grado 1.

La teoria del grafico chiama un grafico vuoto in cui non esiste un singolo bordo. Un grafico completo è un grafico ordinario in cui due vertici sono adiacenti.

I grafici ponderati sono grafici, a cui vertici o archi (archi) o ai vertici e ai bordi (archi) immediatamente, alcuni numeri sono assegnati. Sono chiamati pesi. La seconda figura mostra un grafico non orientato i cui bordi sono ponderati.

Conta: isomorfismo

Il concetto di isomorfismo è usato in matematica. In particolare, la teoria dei grafi la definisce come segue: due grafici U e V sono isomorfi se c'è una biiezione tra gli insiemi dei loro vertici in questi grafici: ogni 2 vertici nel grafico U sono collegati da un bordo se e solo se lo stesso nel grafico V vertici (che possono essere chiamati in modo diverso). La figura seguente mostra due grafici isomorfi, in cui tra i vertici dipinti negli stessi colori sia nel primo che nel secondo grafico, vi è la biiezione sopra descritta.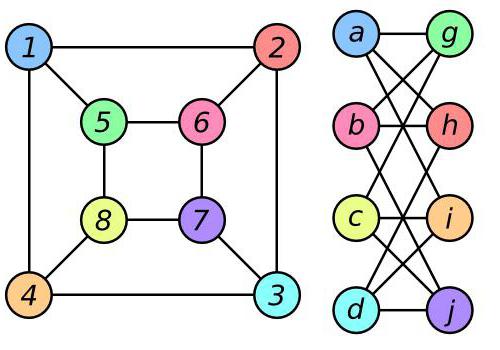

Percorsi e cicli

Un percorso in un grafo orientato o orientato è una sequenza di spigoli, in cui ogni successivo inizia dal vertice in cui termina quello precedente. Un percorso semplice è uno in cui tutti i vertici, escluso, forse, l'iniziale e il finale e i bordi sono diversi. Un ciclo nel digrafo è un percorso i cui vertici iniziale e finale coincidono e che include almeno un bordo. Un ciclo in un grafo non orientato è un percorso che contiene almeno tre bordi diversi. Nella seconda figura, il ciclo è, ad esempio, il percorso (3, 1), (6, 3), (1, 6).

La teoria dei grafi nella programmazione è usata per costruire schemi grafici di algoritmi.