Matematica superiore: un piano nello spazio
Il secondo dopo la linea retta un elemento importante della geometria spaziale è l'aereo. La capacità di descriverlo mediante l'equazione consente di calcolare gli angoli e le altezze spaziali per varie forme tridimensionali. In questo articolo, diamo tutti i tipi di equazioni che descrivono un piano nello spazio. Considerare anche le possibili opzioni per la disposizione reciproca dei piani.
Concetto geometrico di un aereo
Nella geometria bidimensionale, il piano non viene considerato, poiché tutti i problemi sono risolti solo nelle coordinate xey. Quando aggiungiamo il terzo asse coordinato z, il piano diventa un elemento geometrico importante.
Il termine "piano" è inteso come un insieme di punti, due dei quali, se collegati, il vettore risultante sarà sempre perpendicolare ad un dato vettore. Questo dato vettore è chiamato normale. La norma svolge un ruolo importante nella descrizione numerica del piano e le sue proprietà sono utilizzate per risolvere vari problemi.
Ad
La figura seguente mostra tre piani nello spazio (blu) che il quarto (rosso) interseca.
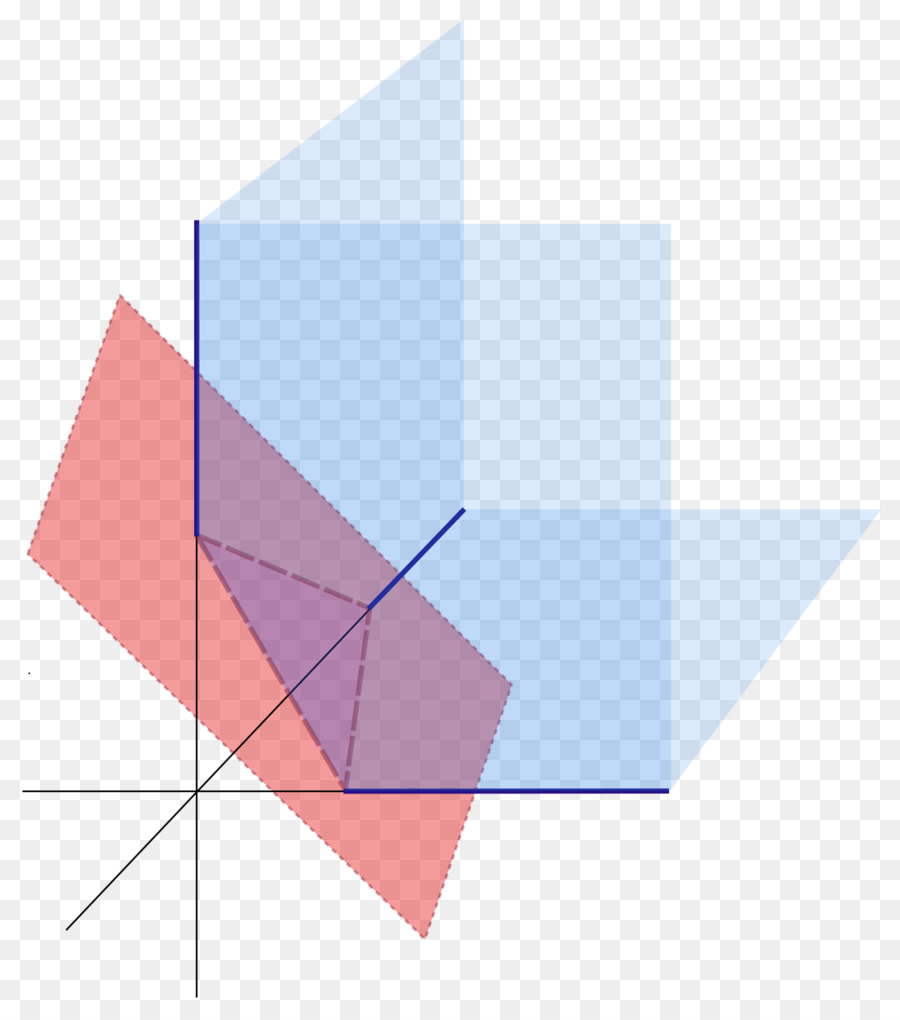
Equazione generale
La definizione sopra riportata aiuterà ad ottenere un'equazione per un piano nello spazio in coordinate. Supponiamo che ci sia un punto con coordinate conosciute Q (x 0 ; y 0 ; z 0 ). È noto che giace in un certo piano, il normale al quale è uguale a n¯ (A; B; C). Supponiamo ora che anche un punto arbitrario M (x; y; z) appartenga a questo piano. Quest'ultimo significa che i vettori QM¯ e n¯ saranno perpendicolari, cioè il loro prodotto scalare scomparirà. Pertanto, possiamo scrivere la seguente uguaglianza:
(QM¯ * n¯) = 0.
Sostituendo le coordinate e aprendo le parentesi, arriviamo all'equazione:
(xx 0 ) * A + (yy 0 ) * B + (zz 0 ) * C = 0 =>
A * x + B * y + C * z + D = 0, dove D = -1 * (A * x 0 + B * y 0 + C * z 0 ).
L'equazione risultante per il piano è chiamata generale. Ha la stessa forma dell'equazione generale per un'equazione diretta su un piano. Si può vedere che i coefficienti di fronte alle variabili x, y e z non sono altro che le coordinate del piano perpendicolare del vettore. Si chiama regia.
Ad
Si noti che se, mentre si ottiene un'equazione generale, un punto specifico Q è sconosciuto e c'è solo il vettore di direzione n¯, si arriva all'equazione per un insieme di piani paralleli che differiscono solo nel parametro D.
Equazione parziale
Quando si descrivono i piani nello spazio, quando vengono forniti specifici assi di coordinate, è più semplice mantenere le costruzioni geometriche se ci sono punti in cui il piano interseca questi assi. Un'espressione che consente di scoprire i valori delle coordinate dell'intersezione del piano con gli assi x, ye è denominata equazione di intervallo. Può essere ottenuto eseguendo alcune trasformazioni matematiche con un'equazione generale.
Supponiamo che la seguente equazione sia nota:
A * x + B * y + C * z + D = 0.
Trasferisci il termine libero D sul lato destro dell'equazione, quindi divide entrambi i lati dell'equazione in modo che l'unità si trovi sulla destra. Abbiamo:
A * x + B * y + C * z = -D =>
x / (- D / A) + y / (- D / B) + z / (- D / C) = 1 o
x / p + y / q + z / r = 1, dove p = -D / A, q = -D / B, r = -D / C.
L'espressione risultante è chiamata un'equazione nei segmenti e le lunghezze dei segmenti tagliati sugli assi x, yez, a partire dal punto (0; 0; 0), hanno rispettivamente i valori p, qe r. Questo può essere controllato come segue: se assumiamo che le coordinate lungo l'asse y e z siano zero, allora x è uguale a q. Cioè, il punto di intersezione con l'asse x ha coordinate (p; 0; 0). Allo stesso modo, argomentando, otteniamo le restanti due coordinate (0; q; 0) e (0; 0; r).
Ad
Equazione vettoriale parametrica
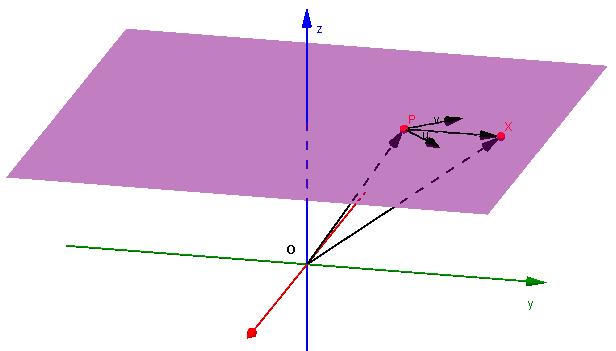
Questo è il terzo importante tipo di equazione che viene spesso utilizzato anche nel problem solving. È stato mostrato sopra che il piano è definito in modo univoco da un punto e un vettore normale. Tuttavia, è possibile determinare questo oggetto bidimensionale geometrico in un modo diverso.
Supponiamo che ci siano due vettori complanari che non sono paralleli tra loro. Li denotiamo con u¯ (a 1 ; b 1 ; c 1 ) e v¯ (a 2 ; b 2 ; c 2 ). È anche noto il punto Q (x 0 ; y 0 ; z 0 ). Quale sarà l'equazione del piano che attraversa questo punto e due vettori?
Puoi rispondere a questa domanda ottenendo un'equazione in generale. Tuttavia, risolveremo questo problema in un altro modo. Ricordiamo che qualsiasi vettore di un piano può essere scomposto in altri due vettori complanari, che appartengono anche a questo piano. Ciò significa che un QP vettore arbitrario, dove P (x; y; z), può essere rappresentato come:
QP¯ = α * u¯ + β * v¯.
Attraversando tutti i punti P del piano, otteniamo i parametri corrispondenti α e β. L'equazione data per un piano si chiama parametrico vettoriale. È spesso registrato in forma di coordinate:
Ad
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a 1 ; b 1 ; c 1 ) + β * (a 2 ; b 2 ; c 2 ).
Si può vedere che questa forma di scrittura del piano è simile all'equazione vettoriale per la retta nei casi bidimensionale e tridimensionale.
Questa espressione può anche essere scritta in modo più esplicito separando le variabili:
x = x 0 + α * a 1 + β * a 2 ;
y = y 0 + α * b 1 + β * b 2 ;
z = z 0 + α * c 1 + β * c 2 .
Queste tre equazioni hanno una forma simile all'equazione parametrica per una linea retta nello spazio. Questo tipo è spesso usato quando si converte un'equazione vettoriale in una comune per un piano.
Piani paralleli
Ci sono solo due opzioni per la posizione relativa dei due piani nello spazio. In questa sezione dell'articolo diamo una condizione quando sono paralleli.
Se le due equazioni del piano sono date in una forma generale, allora il loro parallelismo è abbastanza semplice. Due piani saranno paralleli se i loro vettori sono tali guide. Supponiamo che ci siano due equazioni:
A 1 * x + B 1 * y + C 1 * z + D 1 = 0;
A 2 * x + B 2 * y + C 2 * z + D 2 = 0.
Perpendicolare a ciascuno dei piani del vettore sono le coordinate:
n 1 ¯ (A 1 ; B 1 ; C 1 );
n 2 ¯ (A 2 ; B 2 ; C 2 ).
Se il vettore n 1 ¯ può essere rappresentato come una moltiplicazione per un numero reale del vettore n 2 ¯, allora entrambi saranno paralleli, cioè:
n 2 ¯ = l * n 1 ¯, dove l è un numero reale.
Un altro modo per determinare il loro parallelismo consiste nel trovare il coseno dell'angolo tra di loro attraverso il prodotto scalare e i moduli dei vettori. Questo coseno dovrebbe essere uguale all'unità, quindi i vettori (i piani) saranno paralleli. La formula corrispondente è:
Ad
cos (φ) = | (n 1 ¯ * n 2 ¯) | / (| n 1 ¯ | * | n 2 ¯ |) = 1.
Se le equazioni dei piani sono date in forma parametrica, allora il parallelismo nello spazio dei piani è anche determinato dalla condizione del parallelismo delle normali per loro. Per trovare i vettori di direzione di queste normali, si dovrebbero prendere i prodotti vettoriali dei vettori che formano ciascun piano.
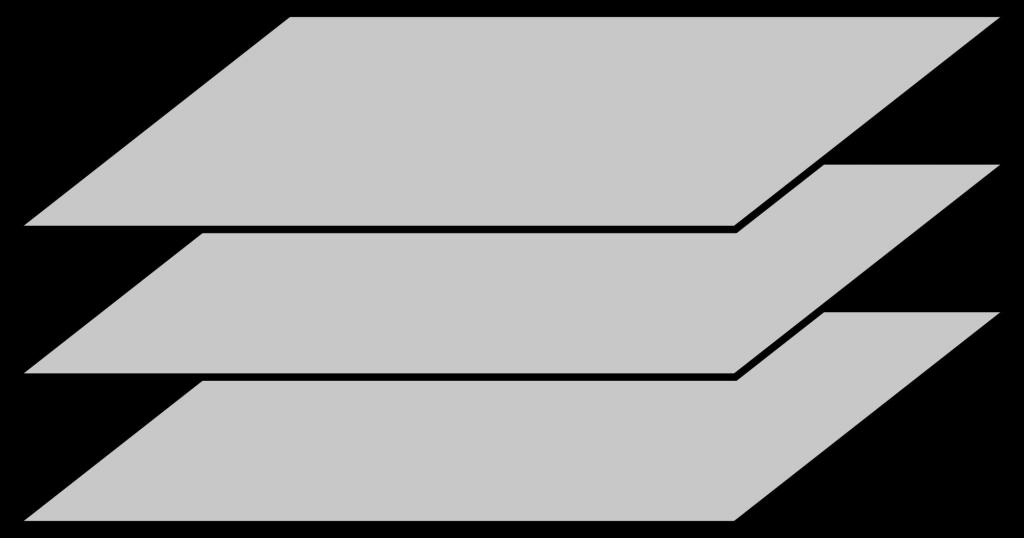
La figura sopra mostra tre piani paralleli tra loro.
Intersezione di aerei
Questa è la seconda versione della disposizione reciproca nello spazio degli aerei. In questo caso, i due piani si intersecano lungo una linea retta che li appartiene. In questo caso, è importante essere in grado di calcolare l'angolo diedro di questa intersezione. È sempre uguale all'angolo tra i corrispondenti vettori guida, cioè tra le perpendicolari dei piani.
Nel paragrafo precedente è già stata fornita una formula che consente di calcolare l'angolo tra le normali. Qui lo apriremo solo scrivendo le coordinate dei vettori n 1 ¯ e n 2 ¯:
φ = arccos (| A 1 * A 2 + B 1 * B 2 + C 1 * C 2 | / (√ (A 1 2 + B 1 2 + C 1 2 ) * √ (A 2 2 + B 2 2 + C 2 2 ))).
Questa formula viene spesso utilizzata per il calcolo degli angoli diedri tra i piani di una piramide o un prisma inclinato.
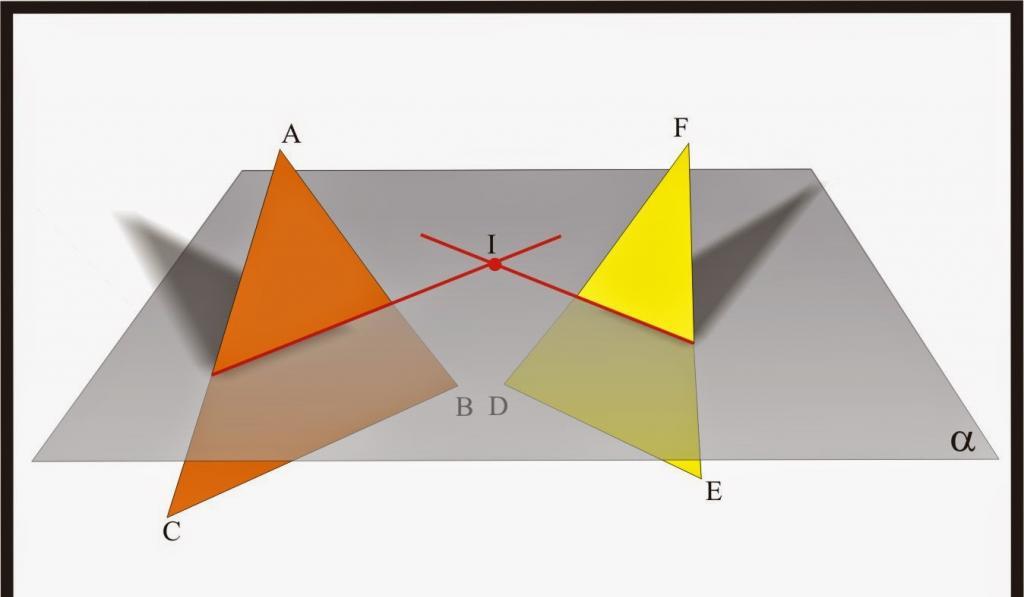
Due piani che intersecano la terza orizzontale sono mostrati nella figura sopra.
Un caso particolare dell'intersezione di due piani è l'angolo φ = 90 o , cioè, vi è una perpendicolarità degli oggetti geometrici considerati. Per determinare la perpendicolarità, non è necessario calcolare l'angolo φ usando la formula un po 'macchinosa di cui sopra, per questo sarà sufficiente calcolare il valore del prodotto scalare n 1 ¯ e n 2 ¯. Per i piani perpendicolari, è zero, cioè:
(n 1 ¯ * n 2 ¯) = A 1 * A 2 + B 1 * B 2 + C 1 * C 2 = 0.
Fascio di aerei
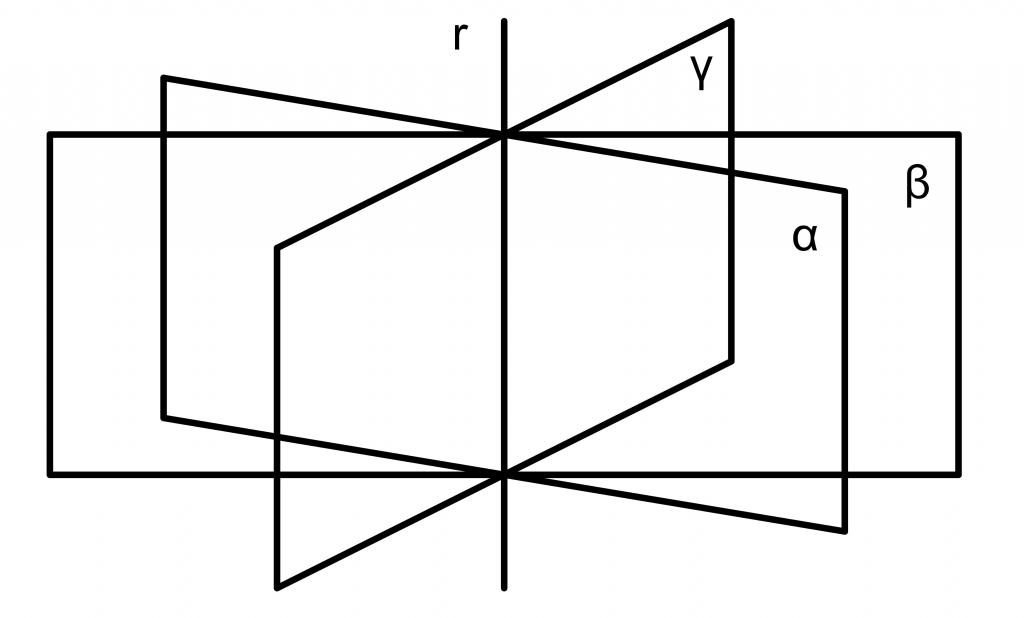
Se due piani si intersecano, tutti i loro punti comuni si trovano su una linea retta. Si noti che uno dei metodi per specificare una retta nello spazio è un sistema di due equazioni generali del piano. Quanti aerei nello spazio possono essere disegnati attraverso una linea retta? Un numero infinito La loro collezione si chiama bundle. L'equazione che descrive questo pacchetto ha la seguente forma:
k 1 * (A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Qui k 1 e k 2 sono numeri arbitrari. Un caso speciale è la situazione in cui uno o entrambi i parametri k non possono assumere il valore zero. Supponiamo che k 1 ≠ 0, quindi l'equazione del raggio possa essere riscritta nella forma:
(A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 / k 1 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Questa uguaglianza descrive tutti i piani del raggio ad eccezione di uno che ha il vettore diretto n 2 ¯ (A 2 ; B 2 ; C 2 ).
Un esempio di un fascio di piani è una raccolta di fogli di un libro aperto.

Successivamente, risolviamo diversi problemi geometrici applicando la conoscenza ottenuta sulle proprietà dei piani nello spazio.
Convertire l'equazione vettoriale parametrica in generale
Data la seguente equazione piana nella forma vettoriale parametrica:
(x; y; z) = (1; 2; 0) + α * (1; 2; 3) + β * (- 1; 3; 0).
È necessario scriverlo come un'equazione generale del piano nello spazio.
Riscriviamolo esplicitamente:
x = 1 + α - β;
y = 2 + 2 * α + 3 * β;
z = 3 * α.
Dall'ultima espressione otteniamo α, quindi la sostituiamo nella prima uguaglianza e esprimiamo β. I parametri trovati sono sostituiti nella seconda equazione, abbiamo:
α = z / 3;
β = 1 - x + z / 3;
y = 2 + 2 * z / 3 + 3 - 3 * x + z =>
y + 3 * x + 5/3 * z - 5 = 0 =>
9 * x + 3 * y + 5 * z -15 = 0.
Quindi, per ottenere un'equazione generale da un vettore parametrico, dobbiamo prima scriverlo esplicitamente e quindi esprimere i parametri in termini di coordinate variabili.
Conversione di un generale in un'equazione vettoriale parametrica
Questo compito è completamente opposto a quello precedente. Considera le tecniche per risolverlo.
Data la seguente equazione:
x-2 * y + 3 * z -1 = 0.
Per cominciare, una coordinata dovrebbe essere espressa in due. Esprimi ad esempio x:
x = 2 * y-3 * z +1.
Ciò significa che qualsiasi punto con coordinate apparterrà al piano:
(2 * y-3 * z +1; y; z).
Ora riscriveremo questa coordinata come la somma di tre vettori, la prima conterrà solo la variabile y, la seconda solo z, e la terza sarà composta esclusivamente da numeri. Abbiamo:
(x; y; z) = (2 * y; y; 0) + (-3 * z; 0; z) + (1; 0; 0).
Si vede che, aprendo questa equazione, otteniamo le coordinate generali per un punto del piano. Ora non resta che calcolare le variabili nel primo e nel secondo vettore e ridefinirle con i parametri α e β. Otteniamo:
(x; y; z) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0; 1).
Abbiamo ottenuto un'equazione in una forma vettoriale parametrica, simile a quella originale.
Immagine dell'aereo nel sistema di coordinate
Il compito è il seguente: secondo un'equazione nota, si dovrebbe disegnare un piano nello spazio. L'equazione corrispondente è:
3 * x - y -4 * z +5 = 0.
Per rappresentare questo piano, è necessario trovare i punti in cui interseca gli assi delle coordinate. Per fare ciò, è possibile ottenere l'equazione corrispondente nei segmenti. Tuttavia, in questo caso, procediamo in modo diverso: poniamo due coordinate uguali a zero e calcoliamo il terzo. Abbiamo:
y = 0; z = 0; x = -5/3;
x = 0; z = 0; y = 5;
x = 0; y = 0; z = 5/4.
Resta da mettere i punti ottenuti sugli assi delle coordinate e disegnare un piano attraverso di essi. La posizione del piano nello spazio è mostrata nella figura sottostante.
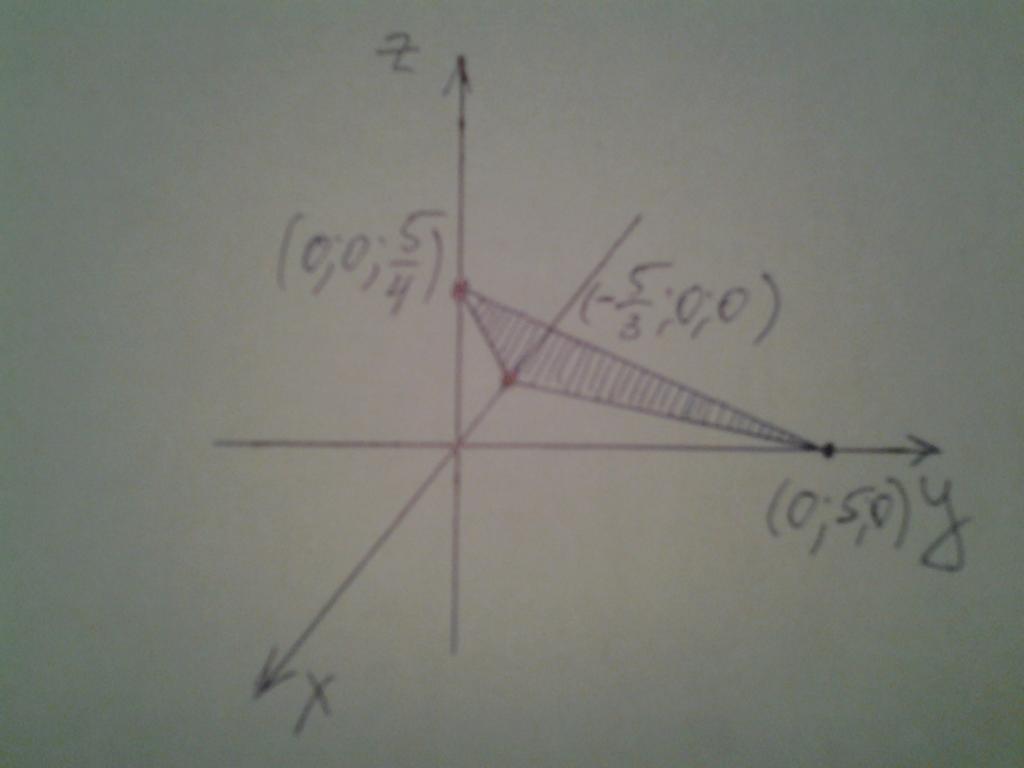
Tre punti e un piano
Lasciate tre punti nello spazio:
M (1; -1; 3);
N (3; 2; -4);
L (2; 5; 0).
È necessario trovare l'aereo che li attraversa.
È noto dalla geometria che tre punti che non giacciono su una linea retta determinano univocamente il piano. La sua equazione può essere composta se troviamo la sua guida vettoriale n °. Sarà uguale al prodotto vettoriale di vettori complanari che giacciono nel piano. Le coordinate dei vettori possono essere ottenute dalle coordinate dei punti, ad esempio:
MN¯ (2; 3; -7);
ML¯ (1; 6; -3).
Il loro prodotto vettoriale darà il vettore n. Calcolo, otteniamo:
n¯ (33; -1; 9).
Prendendo ad esempio il punto M, otteniamo l'equazione generale nella forma:
33 * x -y + 9 * z - 61 = 0.
È possibile sostituire le coordinate dei punti N e L nell'equazione e assicurarsi che l'uguaglianza sia valida.