Come calcolare gli angoli tra i vettori?

Quando si studia la geometria, sorgono molte domande sul tema dei vettori. Lo studente ha particolari difficoltà quando si tratta di trovare angoli tra i vettori.

Termini di base

Prima di considerare gli angoli tra i vettori, è necessario acquisire familiarità con la definizione di un vettore e il concetto di un angolo tra i vettori.

Un vettore è un segmento che ha una direzione, cioè un segmento per il quale sono definiti il ​​suo inizio e la sua fine.

L'angolo tra due vettori su un piano che hanno un inizio comune è chiamato il più piccolo degli angoli, per la quantità di cui si desidera spostare uno dei vettori attorno a un punto comune, in una posizione in cui le loro direzioni coincidono.

Formula per risolvere

Avendo capito cos'è un vettore e come viene determinato il suo angolo, possiamo calcolare l'angolo tra i vettori. La formula della soluzione per questo è abbastanza semplice, e il risultato della sua applicazione sarà il valore del coseno dell'angolo. Secondo la definizione, è uguale al particolare prodotto scalare di vettori e al prodotto delle loro lunghezze.

Il prodotto scalare dei vettori è considerato come la somma delle corrispondenti coordinate dei vettori dei fattori moltiplicate l'una dall'altra. La lunghezza del vettore, o il suo modulo, è calcolata come radice quadrata dalla somma dei quadrati delle sue coordinate.

Avendo ottenuto il valore del coseno dell'angolo, la grandezza dell'angolo stesso può essere calcolata usando una calcolatrice o usando la tabella trigonometrica.

esempio

Una volta compreso come calcolare l'angolo tra i vettori, la soluzione del problema corrispondente diventerà semplice e diretta. Ad esempio, vale la pena considerare il semplice compito di trovare la grandezza dell'angolo.

Prima di tutto, sarà più conveniente calcolare il necessario per risolvere i valori delle lunghezze dei vettori e del loro prodotto scalare. Usando la descrizione presentata sopra, otteniamo:

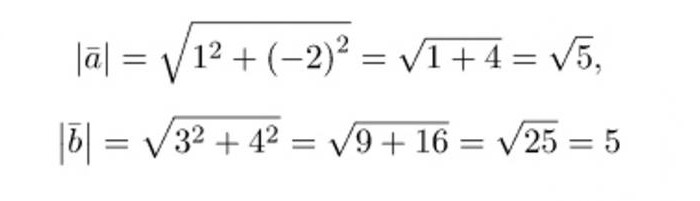
Sostituendo i valori ottenuti nella formula, calcoliamo il coseno dell'angolo desiderato:

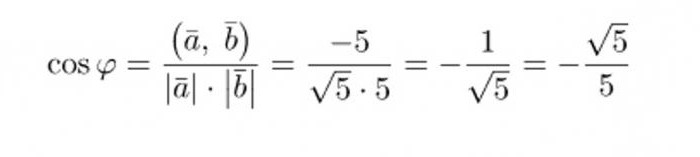
Questo numero non è uno dei cinque valori comuni del coseno, quindi per ottenere l'angolo, dovrai usare la calcolatrice o la tabella trigonometrica Bradis. Ma prima di ottenere l'angolo tra i vettori, la formula può essere semplificata per sbarazzarsi del segno extra negativo:

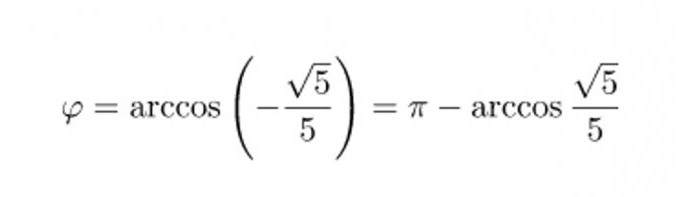
La risposta finale per mantenere l'accuratezza può essere lasciata in questa forma, e puoi calcolare l'angolo in gradi. Secondo la tabella di Bradis, il suo valore sarà di circa 116 gradi e 70 minuti, e il calcolatore mostrerà il valore di 116,57 gradi.

Calcola l'angolo nello spazio n-dimensionale

Quando si considerano due vettori in spazio tridimensionale è molto più difficile capire quale angolo è in questione se non giace sullo stesso piano. Per semplificare la percezione, puoi disegnare due segmenti che si intersecano, che formano l'angolo più piccolo tra loro, e sarà quello desiderato. Nonostante la presenza della terza coordinata nel vettore, il processo di calcolo degli angoli tra i vettori non cambierà. Calcola il prodotto scalare e i moduli dei vettori, l'arco coseno del loro privato e sarà la risposta a questo problema.

Nella geometria, ci sono spesso problemi con spazi che hanno più di tre dimensioni. Ma per loro, l'algoritmo per trovare la risposta sembra lo stesso.

Differenza tra 0 e 180 gradi

Uno degli errori più comuni quando si scrive una risposta a un problema progettato per calcolare l'angolo tra i vettori è la decisione di annotare che i vettori sono paralleli, cioè che l'angolo desiderato è 0 o 180 gradi. Questa risposta non è corretta.

Avendo ottenuto il valore dell'angolo di 0 gradi in base ai risultati della decisione, la risposta corretta sarebbe quella di designare i vettori come codiretti, cioè i vettori avranno la stessa direzione. Nel caso di 180 gradi, i vettori saranno diretti in senso opposto.

Vettori specifici

Trovando gli angoli tra i vettori, puoi trovare uno dei tipi speciali, oltre a quelli codirectional e opposti diretti sopra descritti.

• Diversi vettori paralleli a un piano sono chiamati complanari.
• I vettori della stessa lunghezza e direzione sono chiamati uguali.
• I vettori che si trovano su una linea retta, indipendentemente dalla direzione, sono chiamati collineari.
• Se la lunghezza del vettore è zero, cioè il suo inizio e la sua fine coincidono, allora si chiama zero, e se è uno, allora è un'unità.