Come calcolare la diagonale del prisma di un quadrilatero dritto?

Un prisma è una figura geometrica volumetrica, le cui caratteristiche e proprietà sono studiate nelle scuole superiori. Di norma, quando lo si studia, vengono considerate quantità come volume e superficie. In questo articolo apriremo una domanda leggermente diversa: diamo un metodo per determinare la lunghezza delle diagonali del prisma con l'esempio di una forma quadrangolare.

Quale cifra si chiama un prisma?

In geometria, viene data la seguente definizione di prisma: è una forma tridimensionale, delimitata da due lati identici poligonali che sono paralleli tra loro e da un numero di parallelogrammi. La figura seguente mostra un esempio di un prisma che soddisfa questa definizione.

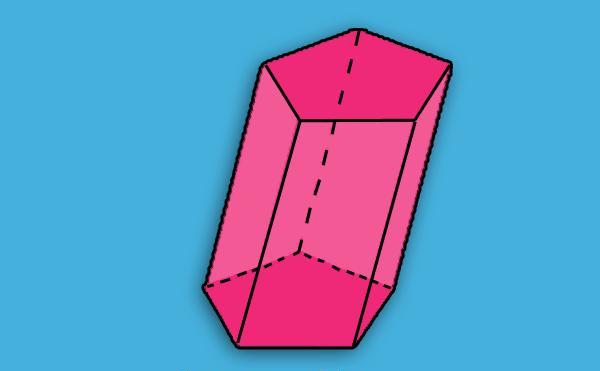
Vediamo che due pentagoni rossi sono uguali tra loro e si trovano su due piani paralleli. Cinque parallelogrammi rosa collegano questi pentagoni in un unico oggetto: un prisma. Due pentagoni sono chiamati le basi della figura, ei suoi parallelogrammi sono facce laterali.

I prismi sono diritti e obliqui, che sono anche chiamati rettangolari e obliqui. La differenza tra loro è negli angoli tra la base e le facce laterali. Per un prisma rettangolare, tutti questi angoli sono 90 ^o .

In base al numero di lati o vertici del poligono alla base, essi parlano di prismi triangolari, pentagonali, quadrangolari e così via. E se questo poligono è corretto, e il prisma stesso è una linea retta, allora una tale forma è chiamata corretta.

Il prisma mostrato nella figura precedente è pentagonale. Di seguito è riportato un prisma rettale pentagonale, che è corretto.

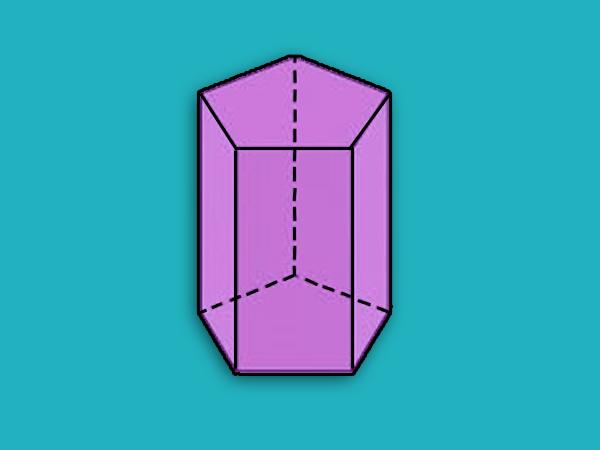
Tutti i calcoli, incluso il metodo per determinare la diagonale del prisma, è conveniente per eseguire esattamente le figure corrette.

Quali elementi caratterizzano il prisma?

Gli elementi della figura sono le parti costituenti che lo formano. In particolare per il prisma, ci sono tre tipi principali di elementi:

• top;
• facce o lati;
• le costole

I volti sono le basi e i piani laterali che rappresentano i parallelogrammi nel caso generale. In un prisma, ciascun lato è sempre di uno di due tipi: o è un poligono o un parallelogramma.

I bordi del prisma sono quei segmenti che limitano ogni lato della figura. Come i bordi, anche i bordi sono di due tipi: appartenenti alla base e alla superficie laterale o appartenenti solo alla superficie laterale. Il primo è sempre due volte più grande del secondo, indipendentemente dal tipo di prisma.

I vertici sono i punti di intersezione dei tre bordi del prisma, due dei quali si trovano nel piano della base, e il terzo appartiene a due facce laterali. Tutti i vertici del prisma sono nei piani della base della figura.

I numeri degli elementi descritti sono collegati in una singola uguaglianza, che ha la seguente forma:

P = B + C - 2.

Qui P è il numero di spigoli, B - top, C - lati. Questa uguaglianza è chiamata teorema di Eulero per un poliedro.

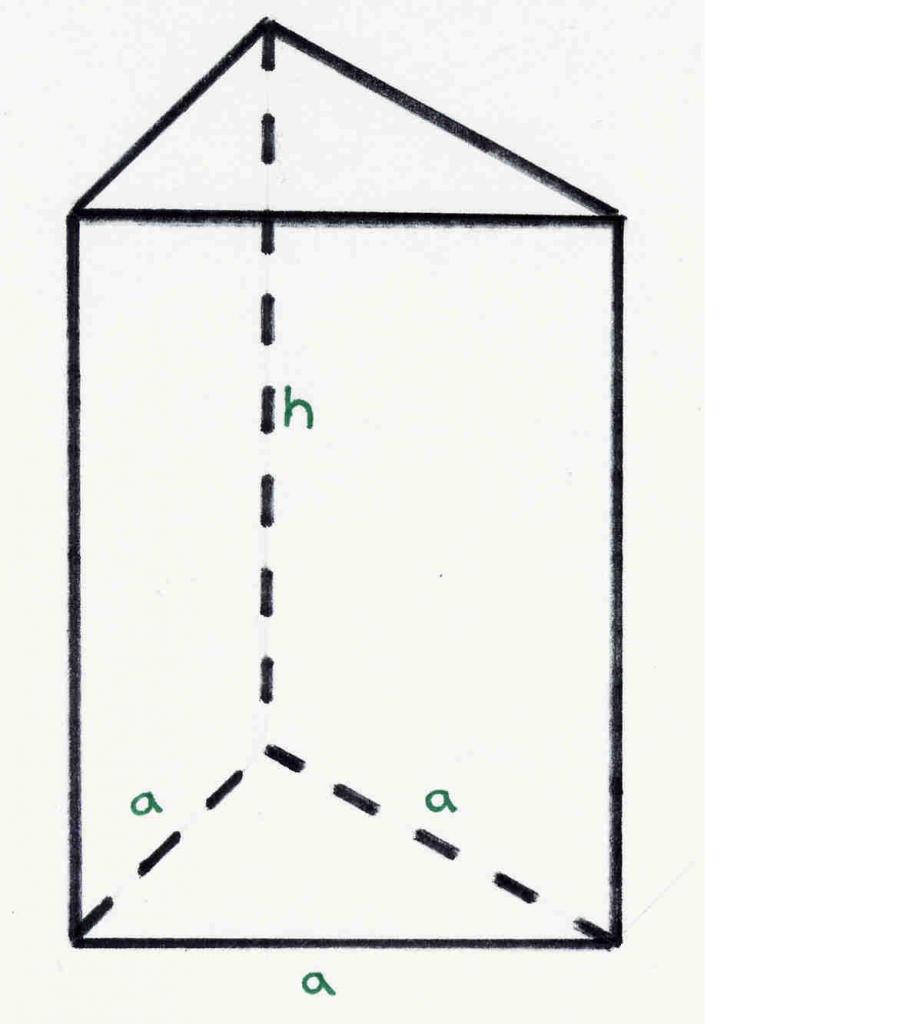
La figura mostra un prisma triangolare corretto. Tutti possono scoprire che ha 6 vertici, 5 lati e 9 spigoli. Questi numeri sono coerenti con il teorema di Eulero.

Prismi diagonali

Dopo proprietà come volume e superficie, in problemi di geometria, si trovano spesso informazioni sulla lunghezza di una data diagonale della figura in esame, che viene data o deve essere trovata utilizzando altri parametri noti. Considera quali sono le diagonali del prisma.

Tutte le diagonali possono essere divise in due tipi:

1. Disteso sul piano dei volti. Collegano i vertici non adiacenti del poligono alla base del prisma o del parallelogramma della superficie laterale. Il valore delle lunghezze di tali diagonali viene determinato in base alla conoscenza delle lunghezze dei bordi corrispondenti e degli angoli tra di loro. Per determinare le diagonali dei parallelogrammi, vengono sempre utilizzate le proprietà dei triangoli.
2. Disteso nel volume del prisma. Queste diagonali collegano picchi non-uno-a-uno di due basi. Queste diagonali sono completamente all'interno della figura. La loro lunghezza è un po 'più difficile da calcolare rispetto al tipo precedente. Il metodo di calcolo prevede la considerazione delle lunghezze dei bordi e della base e dei parallelogrammi. Per i prismi retti e regolari, il calcolo è relativamente semplice, poiché viene eseguito utilizzando il teorema di Pitagora e le proprietà delle funzioni trigonometriche.

Di seguito sono riportati esempi di calcolo di varie diagonali.

Lati diagonali di un prisma quadrangolare dritto

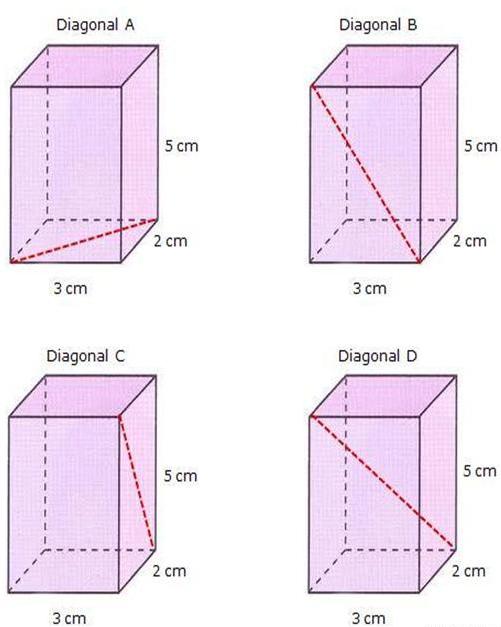
La figura in alto mostra quattro prismi retti identici e vengono indicati i parametri dei loro bordi. Sui prismi di Diagonale A, Diagonale B e Diagonale C, la linea tratteggiata rossa mostra la diagonale di tre diverse facce. Poiché il prisma è dritto con un'altezza di 5 cm, e la sua base è rappresentata da un rettangolo con lati di 3 cm e 2 cm, è facile trovare le diagonali marcate. Per fare ciò, usa il teorema di Pitagora.

La lunghezza della diagonale della base del prisma (Diagonale A) è uguale a:

D _A = √ (3 ² +2 ² ) = √13 ≈ 3.606 cm.

Per la faccia laterale del prisma, la diagonale è (vedi Diagonale B):

D _B = √ (3 ² +5 ² ) = √34 ≈ 5.831 cm.

Infine, la lunghezza di un'altra diagonale laterale è uguale (vedi Diagonale C):

D _C = √ (2 ² +5 ² ) = √29 ≈ 5,385 cm.

Lunghezza della diagonale interna

Ora calcoliamo la lunghezza della diagonale del prisma quadrilatero, che è mostrato nella figura precedente (Diagonale D). Non è così difficile farlo se si nota che è un'ipotenusa di un triangolo, in cui l'altezza del prisma (5 cm) e la diagonale D _A mostrata nella figura in alto a sinistra (Diagonale A) saranno le gambe. Quindi otteniamo:

D _D = √ (D _A ² +5 ² ) = √ (2 ² +3 ² +5 ² ) = √38 ≈ 6,164 cm.

Prisma quadrangolare corretto

La diagonale di un prisma regolare, la cui base è un quadrato, viene calcolata nello stesso modo dell'esempio sopra. La formula corrispondente è:

D = √ (2 * a ² + c ² ).

Dove a e c sono le lunghezze del lato di base e del bordo laterale, rispettivamente.

Si noti che nei calcoli abbiamo usato solo il teorema di Pitagora. Per determinare le lunghezze delle diagonali dei prismi regolari con un numero elevato di vertici (pentagonale, esagonale e così via), è già necessario utilizzare le funzioni trigonometriche.