Come calcolare i limiti delle sequenze?
La matematica è la scienza che costruisce il mondo. Come scienziato e una persona semplice, nessuno può farne a meno. In primo luogo, ai bambini piccoli viene insegnato a contare, poi aggiungere, sottrarre, moltiplicare e dividere, le designazioni delle lettere entrano in gioco al liceo e nella più vecchia non possono farne a meno.
Ma oggi parleremo di ciò su cui tutta la famosa matematica è costruita. Sulla comunità di numeri chiamati "limiti di sequenza".
Quali sono le sequenze e dove è il loro limite?
Il significato della parola "sequenza" non è difficile da interpretare. Questa è la costruzione di cose in cui qualcuno o qualcosa è disposto in un certo ordine o coda. Ad esempio, la coda per i biglietti per lo zoo - è una sequenza. E può essere solo uno! Se, per esempio, si guarda la coda nello store, questa è una sequenza. E se una persona lascia improvvisamente questa linea, allora questa è un'altra linea, un altro ordine.
La parola "limite" è anche facilmente interpretabile - questa è la fine di qualcosa. Tuttavia, in matematica, i limiti delle sequenze sono quei valori sulla linea numerica a cui tende una sequenza di numeri. Perché cerca e non finisce? Tutto è semplice, la linea numerica non ha fine e la maggior parte delle sequenze, come i raggi, hanno solo l'inizio e assomigliano a questo:
x 1 , x 2 , x 3 , ... x n ...
Quindi la definizione di una sequenza è una funzione dell'argomento naturale. In parole più semplici, è una serie di membri di alcuni set.
Come viene costruita una sequenza numerica?
L'esempio più semplice di una sequenza numerica potrebbe essere simile a questo: 1, 2, 3, 4, ... n ...
Nella maggior parte dei casi, per scopi pratici, le sequenze sono costruite da numeri e ogni successivo membro della serie, indicato da X, ha il proprio nome. Ad esempio:
x 1 - il primo membro della sequenza;
x 2 - il secondo membro della sequenza;
x 3 - il terzo membro;
...
x n è l'ennesimo termine.
Nei metodi pratici, la sequenza è data dalla formula generale, in cui vi è una variabile. Ad esempio:
X n = 3n, quindi la serie numerica stessa avrà questo aspetto:
x 1 = 3;
x 2 = 6;
x 3 = 9;
e così via
Non dovresti dimenticare che nella registrazione generale delle sequenze puoi usare qualsiasi lettera latina, non solo X. Ad esempio: y, z, k, ecc.
Progressione aritmetica come parte delle sequenze
Prima di cercare i limiti delle sequenze, è consigliabile immergersi più profondamente nel concetto stesso di una tale serie numerica, che tutti hanno incontrato nelle classi medie. Una progressione aritmetica è una serie di numeri in cui la differenza tra membri vicini è costante.
Il compito: "Sia un 1 = 15, e il passo della progressione di una serie numerica d = 4. Costruisci i primi 4 membri di questa serie. "
Soluzione: 1 = 15 (per condizione) - il primo membro della progressione (serie di numeri).
a 2 = 15 + 4 = 19 è il secondo membro della progressione.
e 3 = 19 + 4 = 23 - il terzo membro.
a 4 = 23 + 4 = 27 è il quarto membro.
Tuttavia, questo metodo è difficile da raggiungere valori elevati, come un 125 .. Soprattutto per questi casi, è stata ricavata una formula conveniente per la pratica: a n = a 1 + d (n - 1). In questo caso, un 125 = 15 + 4 (125-1) = 511.
Tipi di sequenze
La maggior parte delle sequenze sono infinite, vale la pena ricordare per tutta la vita. Esistono due tipi interessanti di serie di numeri. Il primo è dato dalla formula a n = (- 1) n . I matematici spesso chiamano questa sequenza un lampeggiatore. Perché? Controlla le sue serie numeriche.
-1, 1, -1, 1, -1, 1, ecc. Con questo esempio, diventa chiaro che i numeri nelle sequenze possono essere facilmente ripetuti.
Sequenza fattoriale È facile intuire: fattoriale è presente nella formula che definisce la sequenza. Ad esempio: a n = (n + 1)!
Quindi la sequenza sarà simile a questa:
a 1 = 1x2 = 2;
a 2 = 1x2x3 = 6;
a 3 = 1x2x3x4 = 24, ecc.
Una sequenza definita da una progressione aritmetica è chiamata infinitamente decrescente se si osserva la disuguaglianza -1 per tutti i suoi membri.
a 1 = - ½;
a 2 = ¼;
a 3 = - 1/8, ecc.
Esiste anche una sequenza composta dallo stesso numero. Quindi, en = 6 consiste in un insieme infinito di sei.
Determinazione del limite di una sequenza
I limiti delle sequenze esistono da tempo in matematica. Certo, meritavano il proprio design competente. Quindi, tempo per imparare la definizione dei limiti delle sequenze. Innanzitutto, considera in dettaglio il limite per una funzione lineare:
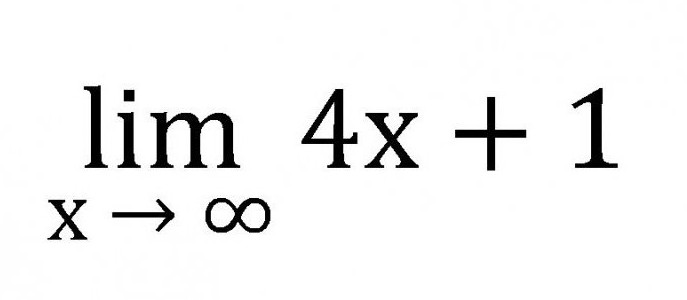
- Tutti i limiti sono abbreviati lim.
- Il record limite è costituito dalla sigla lim, una variabile tendente a un certo numero, zero o infinito, e anche dalla funzione stessa.
È facile capire che la definizione del limite di una sequenza può essere formulata come segue: è un certo numero a cui tutti i membri della sequenza si avvicinano all'infinito. Un semplice esempio: a x = 4x + 1. Quindi la sequenza stessa apparirà come questa.
5, 9, 13, 17, 21 ... x ...
Quindi, questa sequenza aumenterà all'infinito e, quindi, il suo limite è uguale a infinito come x → ∞, e questo dovrebbe essere scritto come:
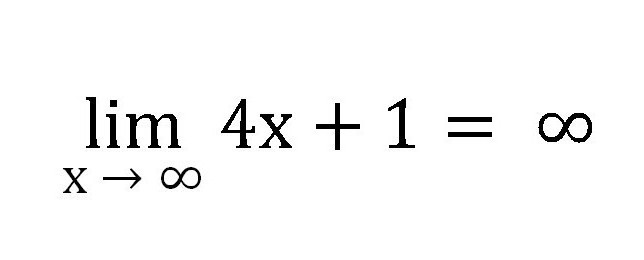
Se prendiamo una sequenza simile, ma x tenderà a 1, otteniamo:
a x = 4x + 1.
Una serie di numeri sarà così: 1.4, 1.8, 4.6, 4.944 e così via. Ogni volta che è necessario sostituire il numero sempre più vicino a uno (0,1, 0,2, 0,9, 0,986). Da questa serie è chiaro che il limite della funzione è cinque.
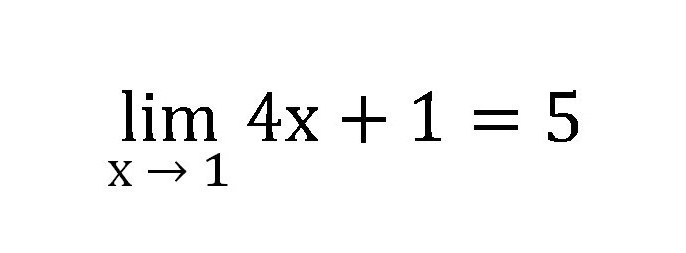
Da questa parte vale la pena ricordare quale sia il limite di una sequenza numerica, la definizione e il metodo per risolvere compiti semplici.
Designazione generale del limite di sequenze
Dopo aver esaminato il limite di una sequenza numerica, la sua definizione e gli esempi, possiamo procedere ad un argomento più complesso. Assolutamente tutti i limiti delle sequenze possono essere formulati con una formula, che di solito viene analizzata nel primo semestre.
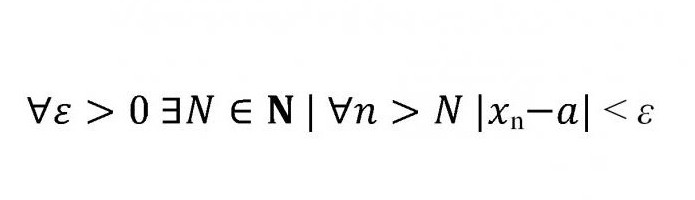
Quindi, cosa significa questo insieme di lettere, moduli e segni di disuguaglianza?
∀ - quantificatore di universalità, sostituendo le frasi "per tutti", "per tutti", ecc.
∃ - quantificatore dell'esistenza, in questo caso significa che esiste un certo valore N appartenente all'insieme numeri naturali.
Un lungo bastone verticale, seguendo N, significa che un dato insieme di N è "tale". In pratica, può significare "tale che", "tale che", ecc.
Poi arriva il modulo. Ovviamente, un modulo è una distanza, che per definizione non può essere negativa. Quindi il modulo di differenza è strettamente inferiore a "epsilon".
Per consolidare il materiale, leggi la formula ad alta voce.
Incertezza e definiteness del limite
Il metodo per trovare il limite delle sequenze, che è stato discusso sopra, è semplice in uso, ma non così razionale nella pratica. Prova a trovare il limite per tale funzione:
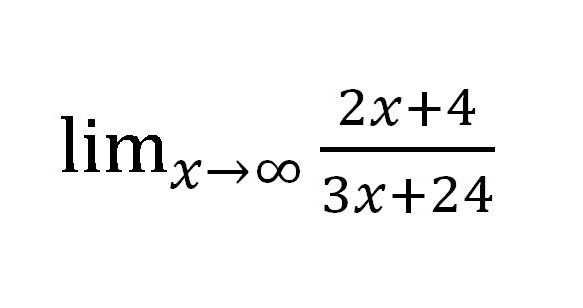
Se sostituiamo diversi valori di "X" (aumentando ogni volta: 10, 100, 1000, ecc.), Nel numeratore otteniamo ∞, ma anche nel denominatore ∞. Risulta una frazione piuttosto strana: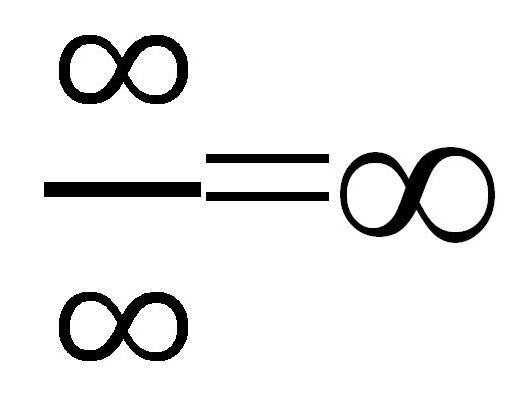 
Ma è davvero? Calcolare il limite di una sequenza numerica in questo caso sembra abbastanza facile. Sarebbe possibile lasciare tutto così com'è, perché la risposta è pronta e è stata ricevuta a condizioni ragionevoli, ma esiste un altro modo specifico per questi casi.
Per cominciare, troviamo la massima potenza nel numeratore di una frazione: è 1, poiché x può essere rappresentato come x 1 .
Ora troviamo il massimo potere nel denominatore. Anche 1.
Dividiamo sia il numeratore che il denominatore in una variabile al massimo grado. In questo caso, la frazione è divisibile per x 1 .
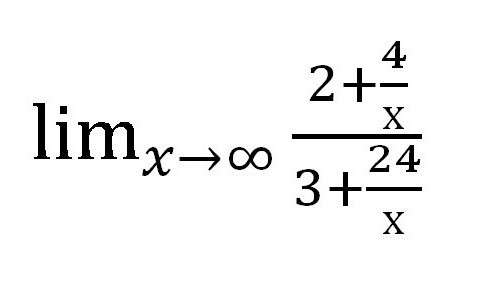
Successivamente, troveremo il valore a cui tende ogni addend contenente la variabile. In questo caso, la frazione. Come x → ∞, il valore di ciascuna delle frazioni tende a zero. Quando si fa un lavoro scritto, vale la pena di fare queste note a piè di pagina:
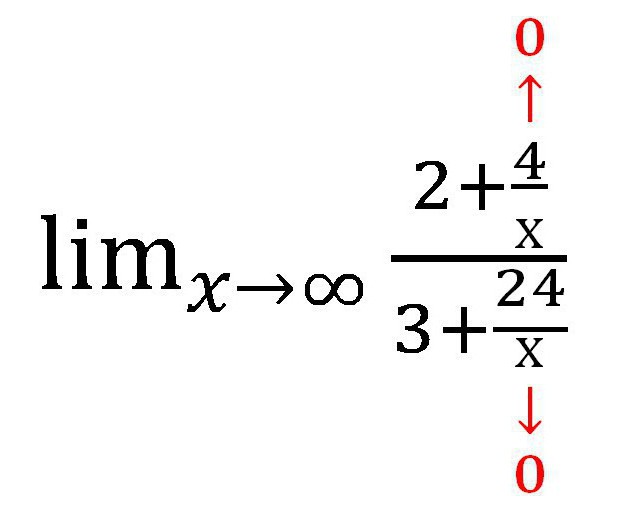
La seguente espressione è ottenuta:
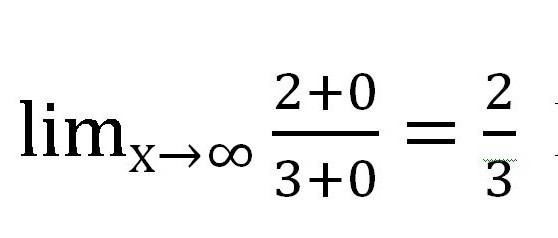
Ovviamente, le frazioni contenenti x non diventano zeri! Ma il loro valore è così piccolo che è completamente permesso non tenerne conto nel calcolo. Infatti, x non sarà mai uguale a 0 in questo caso, perché zero non può essere diviso.
Cos'è un quartiere?
Supponiamo che un professore abbia a sua disposizione una sequenza complessa, data, ovviamente, da una formula non meno complessa. Il professore ha trovato la risposta, ma è adatto? Dopotutto, tutte le persone hanno torto.
Auguste Cauchy ai suoi tempi ha trovato un ottimo modo per dimostrare i limiti delle sequenze. Il suo metodo era chiamato a operare nel quartiere.
Supponiamo che ci sia un punto a, il suo vicinato in entrambe le direzioni sulla linea numerica sia ε ("epsilon"). Poiché l'ultima variabile è la distanza, il suo valore è sempre positivo.
Ora definiamo una sequenza x n e assumiamo che il decimo termine della sequenza (x 10 ) entra nel quartiere di a. Come scrivere questo fatto in linguaggio matematico?
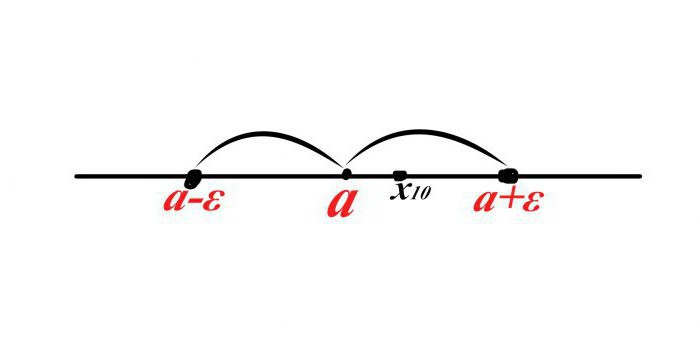
Supponiamo che x 10 sia alla destra del punto a, quindi la distanza è x 10 -a <ε, tuttavia, se posizioni "X decimo" a sinistra del punto a, allora la distanza sarà negativa, ma questo è impossibile, quindi dovresti aggiungere il lato sinistro della disuguaglianza a Otteniamo | x 10 -a | <ε.
Ora è il momento di chiarire in pratica quella formula, che è stata menzionata sopra. Un certo numero a è giustamente chiamato il punto finale della sequenza se per uno qualsiasi dei suoi limiti la disuguaglianza ε> 0 è soddisfatta, e l'intero vicinato ha il proprio numero naturale N, tale che tutti i membri della sequenza con numeri più significativi saranno all'interno della sequenza | x n - a | <ε .
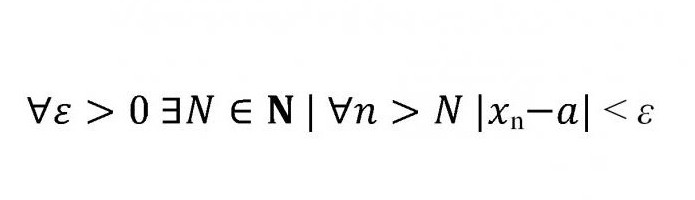
Con tale conoscenza, è facile implementare una soluzione ai limiti di una sequenza, per provare o confutare una risposta pronta.
teorema
Limiti di sequenza I teoremi sono una componente importante della teoria, senza la quale la pratica è impossibile. Ci sono solo quattro teoremi principali, ricordando quali, a volte è possibile facilitare il corso di una soluzione o di una prova:
- L'unicità del limite della sequenza. Il limite per qualsiasi sequenza può essere solo uno o non del tutto. Lo stesso esempio con la coda, che può avere solo una fine.
- Se una serie di numeri ha un limite, la sequenza di questi numeri è limitata.
- Il limite della somma (differenza, prodotto) delle sequenze è uguale alla somma (differenza, prodotto) dei loro limiti.
- Il limite del quoziente dalla divisione di due sequenze è uguale al quoziente dei limiti se e solo se il denominatore non svanisce.
Prova di sequenze
A volte è necessario risolvere un problema inverso, per dimostrare un dato limite di una sequenza numerica. Considera un esempio.
Dimostra che il limite della sequenza data dalla formula è zero.
Secondo la regola discussa sopra, per ogni sequenza la disuguaglianza | x n deve essere soddisfatta - a | <ε. Sostituire il valore specificato e il punto di riferimento. Otteniamo:
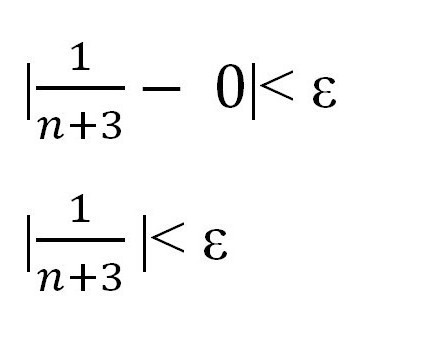
Esprimi n attraverso "epsilon" per mostrare l'esistenza di un certo numero e dimostrare l'esistenza di una sequenza limite.
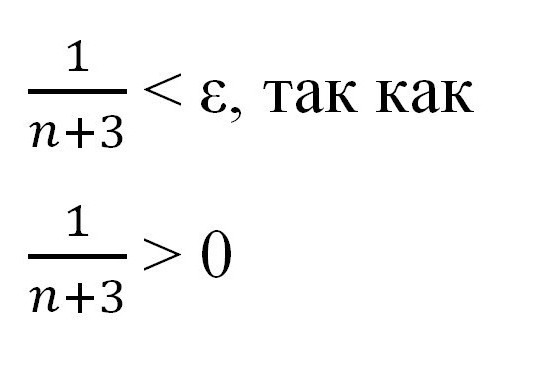
A questo punto, è importante ricordare che "epsilon" e "en" sono numeri positivi e non nulli. Ora puoi continuare a trasformare ulteriormente usando la conoscenza delle disuguaglianze ottenute al liceo.
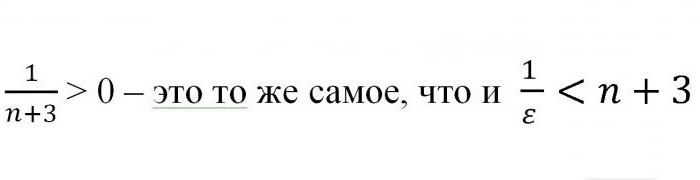
Da ciò risulta che n> -3 + 1 / ε. Poiché vale la pena ricordare che stiamo parlando di numeri naturali, il risultato può essere arrotondato mettendolo tra parentesi quadre. Quindi, è stato dimostrato che per qualsiasi valore del vicinato "epsilon" del punto a = 0 c'era un valore tale che la disuguaglianza iniziale regge. Da questo possiamo tranquillamente affermare che il numero a è il limite di una determinata sequenza. Cosa era necessario per dimostrare.
Con un metodo così conveniente, si può dimostrare il limite di una sequenza numerica, per quanto complessa possa sembrare a prima vista. La cosa principale - non fatevi prendere dal panico alla vista del lavoro.
O forse non lo è?
L'esistenza di una sequenza limite è facoltativa nella pratica. Puoi facilmente trovare una tale serie di numeri che non hanno davvero fine. Ad esempio, lo stesso lampeggiatore x n = (-1) n . è ovvio che una sequenza composta da due soli numeri, ripetendo ciclicamente, non può avere un limite.
La stessa storia viene ripetuta con sequenze composte da un numero, frazionario, avente nel corso dell'incertezza dei calcoli di qualsiasi ordine (0/0, ∞ / ∞, ∞ / 0, ecc.). Tuttavia, va ricordato che anche il calcolo sbagliato ha luogo. A volte il limite delle sequenze aiuterà a ricontrollare le proprie soluzioni.
Sequenza monotona
Sopra abbiamo considerato diversi esempi di sequenze, i metodi per risolverli, e ora proveremo a prendere un caso più specifico e chiamarlo "sequenza monotona".
Definizione: è corretto chiamare qualsiasi sequenza in modo monotono crescente se la rigorosa disuguaglianza x n <x n +1 vale per essa . Inoltre, qualsiasi sequenza viene giustamente chiamata monotona decrescente se la disuguaglianza x n > x n +1 vale per essa .
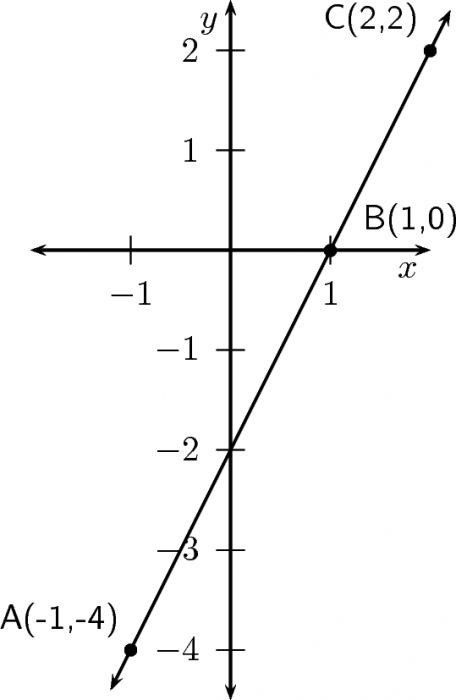
Insieme a queste due condizioni, ci sono anche disuguaglianze deboli simili. Di conseguenza, x n ≤ x n +1 (sequenza non decrescente) e x n ≥ x n +1 (sequenza non crescente).
Ma è più facile capirlo con esempi.
La sequenza data dalla formula x n = 2 + n forma la seguente serie di numeri: 4, 5, 6, ecc. Si tratta di una sequenza monotonicamente crescente.
E se prendiamo x n = 1 / n, otteniamo una serie: 1/3, ¼, 1/5, ecc. Si tratta di una sequenza monotonicamente decrescente.
Limite della sequenza convergente e limitata
Sequenza limitata: una sequenza che ha un limite. Una sequenza convergente è una serie di numeri che ha un limite infinitamente piccolo.
Quindi, il limite di una sequenza limitata è qualsiasi o valido numero complesso Ricorda che può esserci un solo limite.
Il limite di una sequenza convergente è una quantità infinitesima (reale o complessa). Se si disegna un diagramma di sequenza, a un certo punto sembrerà che converga, si sforzasse di tornare a un certo valore. Da qui il nome - sequenza convergente.
Limite monotono
Il limite per una tale sequenza può o non può essere. All'inizio è utile capire quando è, da cui si può spingere quando si prova l'assenza di un limite.
Tra le sequenze monotone emettono convergenti e divergenti. La convergenza è una sequenza formata dall'insieme x e ha un limite reale o complesso nell'insieme. Divergente - una sequenza che non ha limiti nel suo insieme (né reale né complesso).
Inoltre, la sequenza converge se la sua immagine geometrica converge i suoi limiti superiore e inferiore.
Il limite di una sequenza convergente in molti casi può essere uguale a zero, poiché ogni sequenza infinitamente piccola ha un limite noto (zero).
Non importa quale sequenza convergente, sono tutti limitati, ma non tutte le sequenze limitate convergono.
La somma, la differenza, il prodotto di due sequenze convergenti è anche una sequenza convergente. Tuttavia, il quoziente può anche essere convergente se è definito!
Varie azioni con limiti
I limiti delle sequenze sono sostanziali (nella maggior parte dei casi) come numeri e numeri: 1, 2, 15, 24, 362, ecc. Si scopre che alcune operazioni possono essere eseguite con limiti.
Innanzitutto, come numeri e numeri, i limiti di ogni sequenza possono essere aggiunti e sottratti. Basato sul terzo teorema sui limiti delle sequenze, vale la seguente uguaglianza: il limite della somma delle sequenze è uguale alla somma dei loro limiti.
In secondo luogo, sulla base del quarto teorema sui limiti delle sequenze, la seguente uguaglianza è vera: il limite del prodotto del n ° numero di sequenze è uguale al prodotto dei loro limiti. Lo stesso vale per la divisione: il limite del quoziente di due sequenze è uguale al quoziente dei loro limiti, a condizione che il limite non sia zero. Dopo tutto, se il limite delle sequenze è uguale a zero, allora otteniamo divisione per zero, che è impossibile.
Proprietà di sequenza
Sembrerebbe che il limite di una sequenza numerica sia già stato analizzato in dettaglio, ma frasi come numeri "infinitamente piccoli" e "infinitamente grandi" sono menzionate più di una volta. Ovviamente, se esiste una sequenza 1 / x, dove x → ∞, allora tale frazione è infinitamente piccola, e se la sequenza è la stessa, ma il limite tende a zero (x → 0), la frazione diventa una quantità infinitamente grande. E tali quantità hanno le loro caratteristiche. Le proprietà del limite di una sequenza con valori piccoli o grandi sono le seguenti:
- La somma di qualsiasi quantità di quantità arbitrariamente piccole sarà anche una piccola quantità.
- La somma di un numero qualsiasi di grandi quantità sarà una quantità infinitamente grande.
- Il prodotto di quantità arbitrariamente piccole è infinitamente piccolo.
- Il prodotto di un numero qualsiasi di grandi numeri è un valore infinitamente grande.
- Se la sequenza originale tende a un numero infinitamente grande, allora la quantità opposta ad essa sarà infinitamente piccola e tende a zero.
In effetti, calcolare il limite di una sequenza non è un compito così difficile se si conosce un semplice algoritmo. Ma i limiti delle sequenze - un argomento che richiede la massima attenzione e perseveranza. Certo, è sufficiente solo per cogliere l'essenza della soluzione di tali espressioni. A partire da piccole, nel tempo è possibile raggiungere grandi vette.