Come calcolare il volume della palla e altre sfumature nei calcoli
Prima di iniziare a studiare il concetto di una palla, qual è il volume di una palla, considerate le formule per il calcolo dei suoi parametri, è necessario richiamare il concetto di un cerchio studiato in precedenza nel corso della geometria. Dopo tutto, la maggior parte delle azioni in spazio tridimensionale sono simili o derivano dalla geometria bidimensionale, corretta per l'aspetto della terza coordinata e del terzo grado.
Cos'è un cerchio?
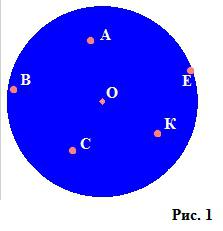
Un cerchio è una figura su un piano cartesiano (mostrato in Figura 1); Molto spesso, la definizione suona come "il luogo di tutti i punti sul piano, la distanza dalla quale a un dato punto (centro) non supera un certo numero non negativo, chiamato raggio".
Come vediamo dalla figura, il punto O è il centro della figura, e l'insieme di tutti i punti che riempiono il cerchio, ad esempio A, B, C, K, E, non sono oltre un raggio specificato (non estendersi oltre il cerchio mostrato in figura . 2).
Ad
Se il raggio è zero, il cerchio si trasforma in un punto.
Comprensione dei problemi
Gli studenti confondono spesso questi concetti. Facile da ricordare disegnando un'analogia. Il cerchio che i bambini torcono nelle lezioni di educazione fisica è un cerchio. Capendo questo o ricordando che le prime lettere di entrambe le parole sono "O", i bambini capiranno mnemonicamente la differenza.
Introduzione del concetto di "palla"

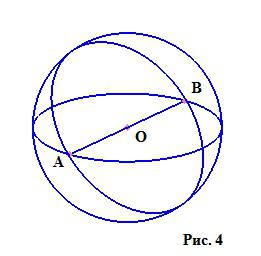
Una palla è un corpo (figura 3), delimitato da una superficie sferica. Quale "superficie sferica" risulterà chiara dalla sua definizione: questa è la posizione geometrica di tutti i punti sulla superficie, la distanza dalla quale a un dato punto (centro) non supera un certo numero non negativo, chiamato raggio. Come si vede, i concetti di un cerchio e di una superficie sferica sono simili, solo gli spazi in cui si trovano differiscono. Se disegniamo una palla nello spazio bidimensionale, otteniamo un cerchio, il cui limite è un cerchio (alla palla il confine è una superficie sferica). Nella figura vediamo una superficie sferica con raggi OA = OB.
Ad
Palla chiusa e aperta
Negli spazi vettoriali e metrici vengono anche considerati due concetti relativi a una superficie sferica. Se la palla include questa sfera in se stessa, allora si chiama chiusa, e in caso contrario, la palla è aperta. Questi sono concetti più "avanzati", sono studiati nelle istituzioni con l'introduzione all'analisi. Per un uso semplice, anche domestico, sono sufficienti le formule studiate nel corso della stereometria delle classi 10-11. Sono concetti che sono accessibili a quasi tutte le persone istruite media che saranno discusse ulteriormente.
Concetti che devi conoscere per i seguenti calcoli
- Raggio e diametro.
- Il raggio della palla e il suo diametro sono determinati allo stesso modo di un cerchio.
- Raggio - un segmento che collega qualsiasi punto sul confine della palla e il punto che è il centro della palla.
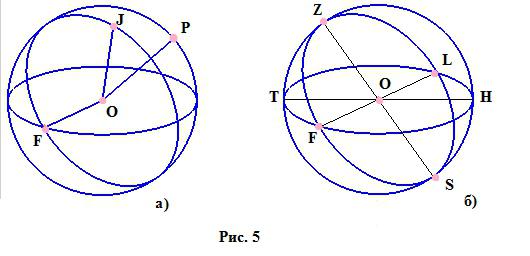
- Diametro - un segmento che collega due punti sul bordo della palla e passa attraverso il suo centro. La Figura 5a mostra chiaramente quali segmenti sono i raggi della palla, e la Figura 5b mostra i diametri della sfera (i segmenti che passano attraverso il punto O).
Sezioni in sfera (palla)
Ogni sezione di una sfera è un cerchio. Se passa attraverso il centro della palla, si chiama un cerchio grande (un cerchio con un diametro AB), le sezioni rimanenti sono piccoli cerchi (un cerchio con un diametro DC).
Ad
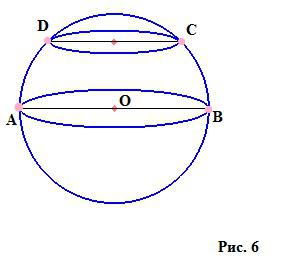
L'area di questi cerchi è calcolata dalle seguenti formule:
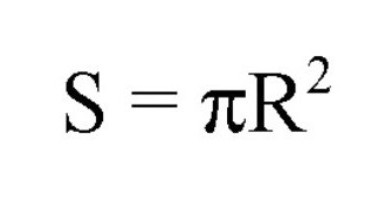
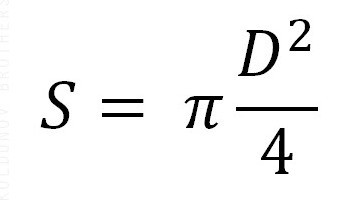
Qui S è la designazione dell'area, R è il raggio, D è il diametro. Anche presente è una costante di 3,14. Ma non confondetelo per calcolare l'area di un cerchio grande usando il raggio o il diametro della sfera (sfera), e per determinare l'area, sono necessarie le dimensioni del raggio di un piccolo cerchio.
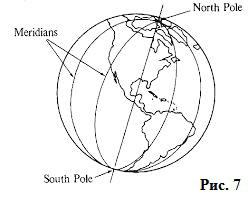
Ci sono innumerevoli sezioni di questo tipo che passano attraverso due punti dello stesso diametro che si trovano sul confine della palla. Ad esempio, il nostro pianeta: due punti ai poli nord e sud, che sono le estremità dell'asse terrestre e, in senso geometrico, le estremità del diametro e i meridiani che passano attraverso questi due punti (Figura 7). Cioè, il numero di cerchi grandi in una sfera tende all'infinito.
Parti di palla
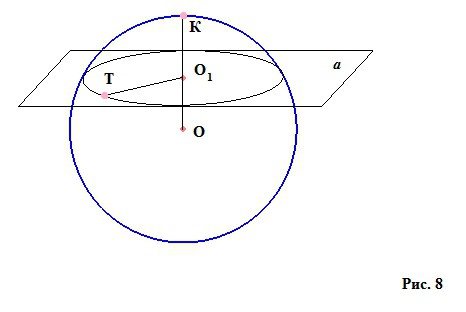
Se si taglia una sfera da una sfera con l'aiuto di un certo piano "pezzo" (Figura 8), allora si chiamerà un segmento sferico o sferico. Avrà un'altezza - perpendicolare dal centro del piano di taglio alla superficie sferica O 1 K. Il punto K sulla superficie sferica, a cui viene l'altezza, è chiamato il vertice del segmento sferico. Un piccolo cerchio con un raggio di O 1 T (in questo caso, secondo la figura, l'aereo non ha attraversato il centro della sfera, ma se la sezione passa attraverso il centro, il cerchio della sezione sarà grande) formato quando il segmento della palla è tagliato, sarà chiamato la base del nostro pezzo palla - un segmento sferico.
Ad
Se connetti ogni punto della base del segmento sferico con il centro della sfera, otteniamo una forma chiamata "settore della sfera".
Se due piani che sono paralleli l'uno all'altro passano attraverso la sfera, allora quella parte della sfera che è racchiusa tra loro è chiamata uno strato sferico (Figura 9, che mostra una sfera con due piani e uno strato sferico separatamente).
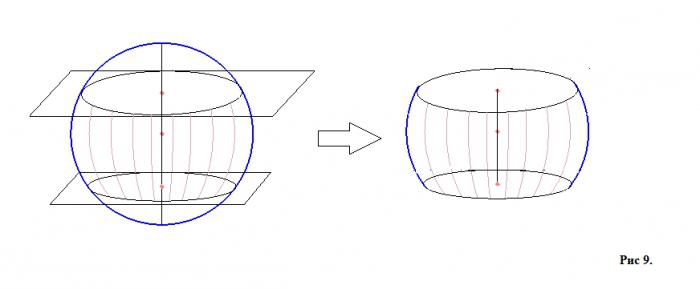
La superficie (la parte evidenziata nella Figura 9 a destra) di questa parte della sfera è chiamata cintura (di nuovo, per una migliore comprensione, si può tracciare un'analogia con il globo, cioè con le sue zone climatiche - artica, tropicale, moderata, ecc.) Ei cerchi di sezione saranno le basi strato di palla. L'altezza dello strato è la parte del diametro disegnato perpendicolare ai piani di taglio dai centri delle basi. C'è anche il concetto di una sfera. Si forma nel caso in cui i piani, che sono paralleli tra loro, non intersecano la sfera, ma la toccano in un punto ciascuno.
Formula per il calcolo del volume della palla e della sua superficie
Una palla è formata ruotando attorno a un diametro fisso di un semicerchio o un cerchio. Per calcolare i vari parametri di questo oggetto non servono troppi dati.
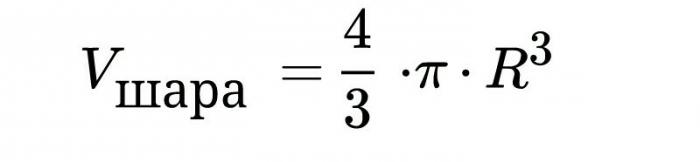
Il volume della palla, la formula per il calcolo che è indicata sopra, è derivata per mezzo di integrazione. Capiremo i punti.
Consideriamo un cerchio in un piano bidimensionale, perché, come detto sopra, è il cerchio a costituire la base della costruzione della palla. Usiamo solo la sua quarta parte (Figura 10). 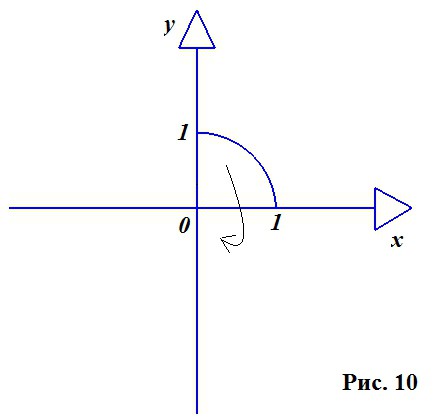
Prendi un cerchio con raggio unitario e centro all'origine. L'equazione di un tale cerchio è la seguente: X 2 + Y 2 = R 2 . Esprimiamo da qui Y: Y 2 = R 2 - X 2 . 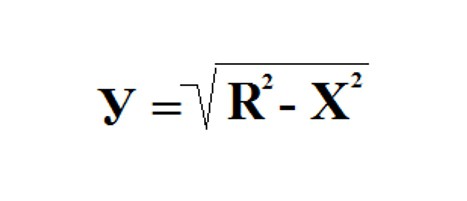
Si noti che la funzione risultante è non negativa, continua e decrescente sul segmento X (0; R), perché il valore di X nel caso in cui consideriamo un quarto di un cerchio, si trova da zero al valore del raggio, cioè a uno.
Ad
La prossima cosa che facciamo è ruotare il nostro quarto di cerchio attorno all'asse x. Di conseguenza, otteniamo un emisfero. Per determinare il suo volume, ricorriamo ai metodi di integrazione.
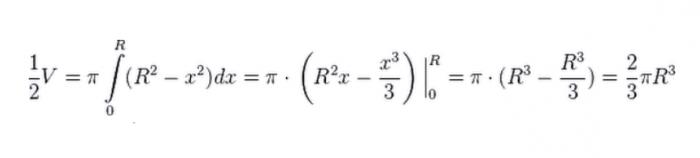
Poiché questo volume è solo un emisfero, raddoppiamo il risultato, da cui otteniamo che il volume della palla è uguale a:
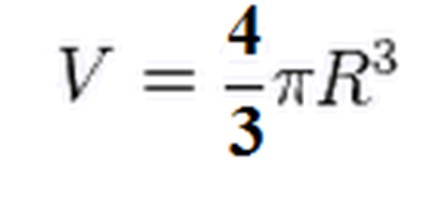
Piccole sfumature
Se è necessario calcolare il volume della palla attraverso il suo diametro, ricorda che il raggio è metà del diametro e sostituisci questo valore nella formula sopra.
Inoltre, la formula per il volume della palla può essere raggiunta attraverso l'area della sua superficie confinante: la sfera. Ricordiamo che l'area della sfera è calcolata dalla formula S = 4πr 2 , integrando ciò, arriviamo anche alla formula sopra per il volume della palla. Dalle stesse formule, si può esprimere il raggio se la condizione del problema contiene un valore di volume.