Come condurre uno studio a funzioni complete

In questo articolo, esamineremo lo schema per studiare una funzione e forniremo anche esempi di studi sugli estremi, la monotonia e gli asintoti di questa funzione.

schema

1. Area di esistenza (DHS).
2. L'intersezione della funzione (se presente) con gli assi delle coordinate, i segni della funzione, la parità, la periodicità.
3. Break points (il loro genere). Continuità. Asintoti verticali.
4. Monotonia e punti estremi.
5. Punti di flesso Convessità.
6. Lo studio della funzione all'infinito, sugli asintoti: orizzontale e obliquo.
7. Tracciare.

Studio della monotonia

Teorema. Se la funzione g è continua su [a, b] , differenziata da (a; b) eg '(x) ≥ 0 (g' (x) ≤0) , xє (a; b) , allora g sta aumentando (diminuendo) di [a, b] .

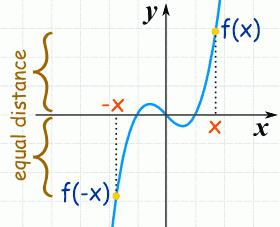
esempio:

y = 1: 3x ³ - 6: 2x ² + 5x.

DHS: xR

y '= x ² + 6x + 5.

Trova intervalli di segni costanti y ' . Poiché y ' è una funzione elementare, può cambiare i segni solo nei punti in cui diventa zero o non esiste. Il suo DHS: xR .

Trova i punti, la cui derivata è 0 (zero):

y '= 0;

x = -1; -5.

Quindi, y cresce su (-∞; -5] e su [-1; + ∞), y scendendo a [1; 2] .

Studio estremo

T. x _{0 è} chiamato il punto massimo (max) sul set A della funzione g quando il valore g (x ₀ ) ≥ g (x), xєA , viene assunto come funzione in questo punto.

T. x _{0 è} chiamato il punto minimo (min) della funzione g sull'insieme A quando il più piccolo g (x ₀ ) ≤ g (x), xєA è assunto come funzione in questo punto .

Sul set A, i punti massimi (max) e minimi (min) sono chiamati i punti estremi g . Tali estremi sono anche definiti estremi assoluti sul set .

Se x ₀ è un punto estremo di g in qualche distretto, allora x ₀ è chiamato punto di estremo locale o locale (massimo o minimo) di g.

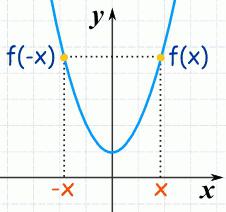
Teorema (condizione richiesta). Se x ₀ è il punto estremo della funzione (locale) g , allora la derivata non esiste o è uguale in questo r 0 (zero).

Definizione. I punti critici sono punti con una derivata inesistente o uguale a 0 (zero). Questi punti dati sono sospetti per extremum.

Teorema (condizione n ° 1). Se la funzione g è continua in un certo intorno di t X ₀ e il segno cambia la sua derivata alla transizione, allora il punto dato è dell'estremo di g .

Teorema (condizione n.2). Lascia che la funzione in un determinato distretto sia differenziabile due volte e g '= 0, e g' '> 0 (g' '<0) , quindi questo punto è il punto della funzione massima (massima) o minima (minima).

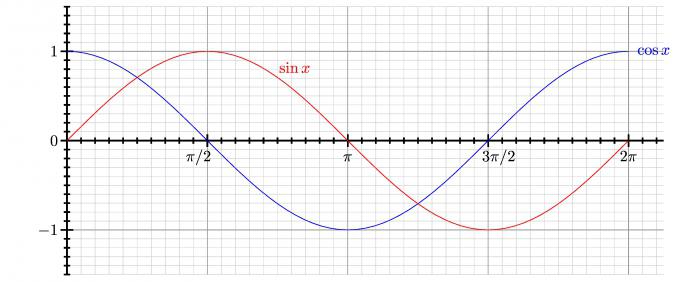
Studio di rigonfiamento

Una funzione è chiamata convesso in giù (o concava) nell'intervallo (a, b) quando il grafico della funzione non è più alto della secante nell'intervallo per ogni x con (a, b) che passa attraverso questi punti .

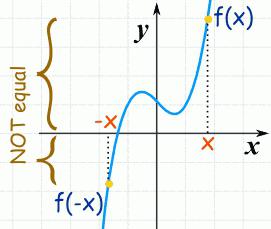
La funzione sarà convessa rigorosamente in giù su (a, b) , se - il grafico si trova sotto la secante sullo spazio vuoto.

La funzione si chiama convesso su (convesso) nell'intervallo (a, b) , se per qualsiasi punto t с (a, b) il grafico della funzione sull'intervallo non è inferiore al secante che passa attraverso le ascisse in questi punti .

La funzione sarà strettamente convessa verso l'alto su (a, b ), se - il grafico dell'intervallo si trova sopra la secante.

Se una funzione in un distretto è un punto è continua e dopo t x ₀ la funzione cambia convessità nella transizione, questo punto è chiamato punto di flesso della funzione.

Test Asymptote

Definizione. Una linea retta è chiamata asintoto g (x) se a una distanza infinita dall'origine delle coordinate si avvicina il punto del grafico della funzione: d (M, l).

Gli asintoti possono essere verticali, orizzontali e obliqui.

La linea verticale con l'equazione x = x ₀ sarà l'asintoto del grafico verticale della funzione g se in t. x _{0 è un} gap infinito, cioè almeno un limite sinistro o destro in questo punto è infinito.

Lo studio della funzione sul segmento sul valore del più piccolo e più grande

Se la funzione è continua su [a, b] , quindi secondo il teorema di Weierstrass c'è il valore più grande e il valore più piccolo su questo segmento, cioè ci sono punti t che appartengono a [a, b] tali che g (x ₁ ) ≤ g (x) <g (x ₂ ), x ₂ є [a, b]. Dai teoremi sulla monotonia e gli estremi, otteniamo il seguente schema per studiare una funzione su un segmento per il valore più piccolo e più grande.

piano

1. Trova la derivata g '(x) .
2. Trova il valore della funzione g in questi punti e alle estremità del segmento.
3. I valori trovati confrontano e selezionano il più piccolo e il più grande.

Nota. Se vuoi studiare la funzione su un intervallo finito (a, b) , o su un infinito (-∞; b); (-∞; + ∞) sul valore massimo e minimo, quindi nel piano, anziché i valori della funzione alle estremità del gap, vengono cercati i confini unilaterali corrispondenti: invece di f (a), f (a +) = limf (x) viene cercato , invece di f (b), f (-b). Quindi puoi trovare le funzioni LDU nell'intervallo, perché gli estremi assoluti non esistono necessariamente in questo caso.

Applicazione del derivato alla soluzione di problemi applicati sull'estremo di certe quantità

1. Esprimere questo valore in termini di altri valori dalla condizione del problema in modo che sia una funzione di una sola variabile (se possibile).
2. Determina il periodo di cambiamento di questa variabile.
3. Effettuare uno studio della funzione sull'intervallo ai valori massimi e minimi.

Task. È necessario costruire una piattaforma rettangolare, utilizzando i metri di griglia, contro il muro in modo che su un lato si adatti al muro e sugli altri tre sia recintato con una griglia. In quale proporzione l'area di tale sito sarà maggiore?

S = xy è una funzione di 2 variabili.

S = x (a - 2x) - funzione della 1a variabile ; x є [0; a: 2].

S = ax - 2x ² ; S '= a - 4x = 0, xєR, x = a: 4.

S (a: 4) = a ² : 8 è il valore più alto;

S (0) = 0.

Trova l'altro lato del rettangolo: = a: 2.

Proporzioni: y: x = 2.

La risposta è L'area più grande sarà pari a 2/8 , se il lato parallelo al muro è 2 volte più grande dell'altro lato.

Funzione di ricerca esempi

Esempio 1

C'è y = x ³ : (1-x) ² . Esegui ricerche.

1. DHS: xє (-∞; 1) U (1; ∞).
2. La forma generale della funzione (né pari né dispari), non è simmetrica rispetto al punto 0 (zero).
3. Segni di funzione La funzione è elementare, quindi può solo cambiare il segno nei punti in cui è 0 (zero) o non esiste.
4. La funzione è elementare, quindi continua su un DHS: (-∞; 1) U (1; ∞).

Gap: x = 1;

Limx ³ : (1- x) ² = ∞ - Una discontinuità del 2 ° tipo (infinito), quindi c'è un asintoto verticale al punto 1;

x = 1 è l'equazione verticale asintotica.

5. y '= x ² (3 - x): (1 - x) ³ ;

DHS (y '): x ≠ 1;

x = 1 - punto critico.

y '= 0;

0; 3 - punti critici.

6. y "= 6x: (1 - x) ⁴ ;

T critico: 1, 0;

x = 0 - m. kink, y (0) = 0.

7. Limx ³ : (1 - 2x + x ² ) = ∞ - non esiste un asintoto orizzontale, ma può essere inclinato.

k = 1 è un numero;

b = 2 è un numero.

Pertanto, vi è un asintoto inclinato y = x + 2 a + ∞ e a - ∞.

Esempio 2

Dato y = (x ² + 1): (x - 1). Per fare e ricercare. Costruisci un grafico.

1. Il dominio dell'esistenza è l'intera linea numerica, ad eccezione di m X = 1 .

2. y interseca OY (se possibile) in m (0; g (0)) . Trova y (0) = -1 - Intersezione OY .

Troviamo i punti di intersezione del grafico con OX risolvendo l'equazione y = 0 . Equazione di radice non ha validità, quindi questa funzione non interseca OX .

3. La funzione è non periodica. Considera l'espressione

g (-x) ≠ g (x) e g (-x) -g (x) . Ciò significa che questa è una funzione generica (né pari né dispari).

4. T. x = 1 gap ha un secondo tipo. In tutti gli altri punti, la funzione è continua.

5. Funzione di esame all'estremità:

(x ² - 2x - 1): (x - 1) ² = y '

e risolvi l'equazione y '= 0.

Quindi, 1 - √2, 1 + √2, 1 - punti critici o punti di possibile estremum. Questi punti dividono la linea numerica in quattro intervalli .

Ad ogni intervallo, la derivata ha un certo segno, che può essere impostato con il metodo degli intervalli o calcolando i valori della derivata nei singoli punti. Sugli intervalli (-∞; 1 - √2 ) U ( 1 + √2 ; ∞) , la derivata positiva significa che la funzione cresce; se xє ( 1 - √2 ; 1) U (1; 1 + √2 ) , allora la funzione diminuisce, perché a questi intervalli la derivata è negativa. Attraverso t. X ₁ quando vai (spostandosi da sinistra a destra) cambia il segno derivato da "+" a "-", quindi, a questo punto c'è un massimo locale, troviamo

y _max = 2 - 2 √2 .

Passando attraverso x _2, cambia il segno derivato da "-" a "+", quindi, a questo punto c'è un minimo locale, e

y _mix = 2 + 2√2.

T. x = 1 non è così estremo.

6. 4: (x - 1) ³ = y ".

A (-∞; 1 ) 0> y " , di conseguenza, su questo intervallo la curva è convessa; se xє ( 1 ; ∞) - la curva è concava. Nel punto 1, la funzione non è definita, quindi questo punto non è un punto di flesso.

7. Dai risultati del paragrafo 4, segue che x = 1 è la curva verticale asintotica.

Asintoti orizzontali sono assenti.

x + 1 = y è l'asintoto inclinato da questa curva. Non ci sono altri asintoti.

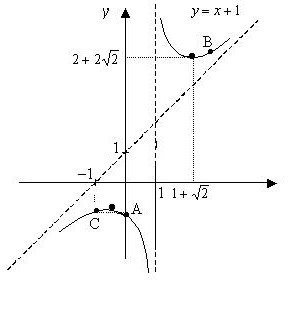
8. Considerando la ricerca condotta, costruiamo un grafico (vedi la figura sopra).