Come trovare la circonferenza: attraverso il diametro e il raggio. Terminologia, formule di base e caratteristiche delle figure

Cerchio: una curva chiusa, i cui punti si trovano alla stessa distanza dal centro. Questa cifra è piatta. Pertanto, la soluzione del problema, la cui domanda è come trovare lunghezza della circonferenza è abbastanza semplice Tutti i metodi disponibili, consideriamo nell'articolo di oggi.

Descrizioni di forma

Oltre a una definizione descrittiva abbastanza semplice, ci sono altre tre caratteristiche matematiche di un cerchio, che a loro volta rispondono già alla domanda su come trovare la lunghezza di un cerchio:

• Consiste dei punti A e B e tutti gli altri, dai quali AB può essere visto ad angolo retto. Il diametro di questa figura è uguale alla lunghezza del segmento considerato.
• Include solo tali punti X, che il rapporto AX / BX è costante e non uguale a uno. Se questa condizione non viene soddisfatta, allora non è un cerchio.
• Consiste di punti, per ognuno dei quali vale la seguente uguaglianza: la somma dei quadrati delle distanze con gli altri due è un dato valore, che è sempre più della metà della lunghezza del segmento tra loro.

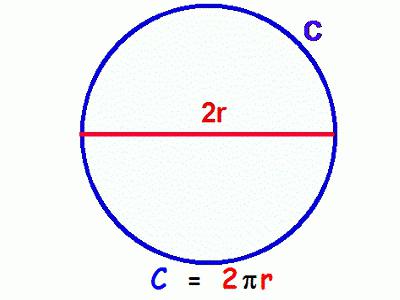
terminologia

Non tutti a scuola avevano un buon insegnante di matematica. Pertanto, la risposta alla domanda su come trovare la lunghezza di un cerchio è complicata dal fatto che non tutti conoscono i concetti geometrici di base. Raggio: un segmento che collega il centro della forma con un punto sulla curva. Un caso speciale nella trigonometria è il cerchio unitario. Un accordo è un segmento che collega due punti di una curva. Ad esempio, questa definizione rientra nella già considerata AB. Il diametro è l'accordo che passa attraverso il centro. Il numero π è uguale alla lunghezza di un singolo semicerchio.

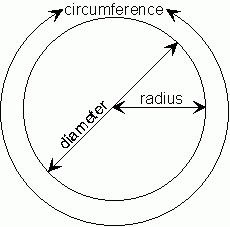
Formule di base

Dalle definizioni segui direttamente le formule geometriche che ti permettono di calcolare le principali caratteristiche del cerchio:

1. La lunghezza è uguale al prodotto del numero π e del diametro. La formula è solitamente scritta come segue: C = π * D.
2. Il raggio è metà del diametro. Può anche essere calcolato calcolando il quoziente dividendo la circonferenza per il doppio numero π. La formula ha questo aspetto: R = C / (2 * π) = D / 2.
3. Il diametro è uguale al quoziente di dividere la circonferenza di π o raddoppiare il raggio. La formula è abbastanza semplice e assomiglia a questa: D = C / π = 2 * R.
4. L'area di un cerchio è uguale al prodotto del numero π e del quadrato del raggio. Allo stesso modo, in questa formula, puoi usare il diametro. In questo caso, l'area sarà uguale al quoziente di divisione del prodotto del numero π e del quadrato del diametro per quattro. La formula può essere scritta come segue: S = π * R ² = π * D 2/4.

Come trovare la circonferenza del diametro

Per semplicità di spiegazione, designiamo le caratteristiche della figura necessaria per il calcolo. Sia C la lunghezza desiderata, D il suo diametro, e il numero π circa uguale a 3.14. Se abbiamo solo una quantità nota, allora il problema può essere considerato risolto. Perché è necessario nella vita? Supponiamo di aver deciso di racchiudere una recinzione per piscina rotonda. Come calcolare il numero richiesto di barre? E qui viene in soccorso l'abilità, come calcolare la lunghezza del cerchio. La formula è la seguente: C = π D. Nel nostro esempio, il diametro viene determinato in base al raggio della piscina e alla distanza richiesta dalla recinzione. Ad esempio, supponiamo che il nostro serbatoio artificiale fatto in casa abbia una larghezza di 20 metri e che posizioneremo i pali a una distanza di dieci metri da esso. Il diametro del cerchio risultante è 20 + 10 * 2 = 40 m Lunghezza - 3,14 * 40 = 125,6 metri. Avremo bisogno di 25 colonne, se il divario tra loro è di circa 5 m.

Lunghezza attraverso il raggio

Come sempre, iniziamo assegnando le lettere a una cerchia. Di fatto, sono universali, quindi i matematici di paesi diversi non hanno bisogno di conoscersi. Supponiamo che C sia la lunghezza di un cerchio, r sia il suo raggio, e π sia approssimativamente uguale a 3.14. La formula guarda in questo caso come segue: C = 2 * π * r. Ovviamente, questa è l'uguaglianza assolutamente corretta. Come abbiamo già capito diametro di un cerchio uguale al suo raggio raddoppiato, quindi questa formula ha questo aspetto. Nella vita, questo metodo può anche tornare utile. Ad esempio, cuociamo una torta in una speciale forma scorrevole. In modo che non si sporchi, abbiamo bisogno di un involucro decorativo. Ma come tagliare un cerchio della giusta misura. Qui la matematica viene in soccorso. Coloro che sanno come scoprire la lunghezza di un cerchio diranno immediatamente che è necessario moltiplicare il numero π per il raggio raddoppiato del modulo. Se il suo raggio è di 25 cm, la lunghezza sarà di 157 centimetri.

Esempi di compiti

Abbiamo già esaminato diversi casi pratici delle conoscenze acquisite su come scoprire la lunghezza di un cerchio. Ma spesso non ci occupiamo di loro, ma con problemi di matematica reali che sono contenuti nel libro di testo. Dopo tutto, per loro, l'insegnante mette dei punti! Pertanto, consideriamo il problema della maggiore complessità. Supponiamo che la circonferenza sia di 26 cm. Come trovare il raggio di una tale figura?

Esempio di soluzione

Per cominciare, scriviamo ciò che ci viene dato: C = 26 cm, π = 3,14. Ricorda anche la formula: C = 2 * π * R. Da esso puoi estrarre il raggio del cerchio. Quindi, R = C / 2 / π. Ora procedere al calcolo diretto. Per prima cosa, dividi la lunghezza per due. Otteniamo 13. Ora dobbiamo dividere per il valore del numero π: 13 / 3,14 = 4,14 cm. È importante non dimenticare di scrivere correttamente la risposta, cioè con unità di misura, altrimenti l'intero significato pratico di tali compiti viene perso. Inoltre, per tale disattenzione, è possibile ottenere un punteggio inferiore di un punto. E non importa quanto fastidioso, devi sopportare questo stato di cose.

La bestia non è così terribile come è dipinta

Quindi abbiamo capito un compito apparentemente difficile. Come si è scoperto, devi solo capire il significato dei termini e ricordare alcune semplici formule. La matematica non è così spaventosa, devi solo fare un piccolo sforzo. Quindi la geometria ti sta aspettando!