Come trovare l'altezza di un trapezio: una formula per tutte le occasioni
Ci sono diverse risposte alla semplice domanda "Come trovare l'altezza di un trapezio?", Tutto perché possono essere dati diversi valori iniziali. Pertanto, le formule varieranno.
Queste formule possono essere ricordate, ma sono facilmente derivabili. È solo necessario applicare i teoremi precedentemente studiati.
Accettato nelle formule
In tutte le registrazioni matematiche sottostanti, tali letture di lettere sono corrette.
| trapezio arbitrario | trapezio isoscele | il nome |
| e | e | base inferiore |
| in | in | base superiore |
| c, d | con | lati |
| n | n | l'altezza |
| m | m | linea di mezzo |
| d 1 d 2 | d 1 | in diagonale |
| s | s | zona |
| α, β | α | angoli inferiori inferiori |
| γ, δ | γ, δ | angoli all'intersezione delle diagonali |
Nei dati di origine: tutti i lati
Per trovare l'altezza di un trapezoide nel caso generale, è necessario utilizzare la seguente formula:
n = √ (c 2 - (((a - c) 2 + c 2 - d 2 ) / (2 (a - c))) 2 ). Numero 1
Non è il più breve, ma è piuttosto raro nei compiti. Di solito puoi usare altri dati.
La formula che ti dice come trovare l'altezza di un trapezio isoscele nella stessa situazione è molto più breve:
n = √ (c 2 - (a - c) 2/4). Numero 2
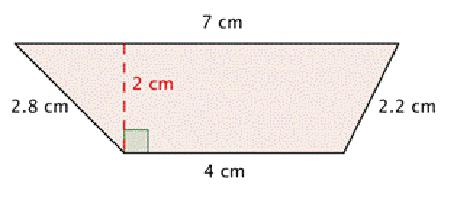
Nel problema sono indicati: i lati e gli angoli nella base inferiore
Si presume che l'angolo α sia adiacente al lato con la designazione "c", rispettivamente, l'angolo β rispetto al lato d. Quindi la formula su come trovare l'altezza del trapezio, in generale, sarà:
Ad
n = c * sin α = d * sin β. Numero 3
Se la figura è isoscele, puoi utilizzare questa opzione:
n = c * sin α = ((a - c) / 2) * tg α. Numero 4
Conosciuto: diagonali e angoli tra di loro
In genere, questi dati sono uniti da valori ancora noti. Ad esempio, la base o la linea di mezzo. Se vengono forniti i motivi, allora la risposta alla domanda su come trovare l'altezza di un trapezio è utile nella seguente formula:
n = (d 1 * d 2 * sin γ) / (a + b) o n = (d 1 * d 2 * sin δ) / (a + b). Numero 5
Questo è per l'aspetto generale della figura. Se viene fornito un isoscene, il record verrà trasformato come segue:
n = (d 1 2 * sin γ) / (a + b) o n = (d 1 2 * sin δ) / (a + b). Numero 6
Quando il problema riguarda la linea centrale di un trapezio, le formule per trovare la sua altezza diventano le seguenti:
n = (d 1 * d 2 * sin γ) / 2m or n = (d 1 * d 2 * sin δ) / 2 m. Stanza 5a.
n = (d 1 2 * sin γ) / 2m or n = (d 1 2 * sin δ) / 2m. Numero 6a.
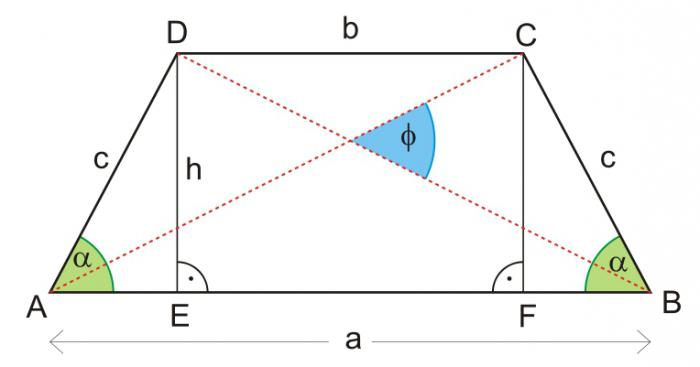
Tra i valori noti: area con basi o linea mediana
Queste sono forse le formule più brevi e semplici per trovare l'altezza di un trapezio. Per una forma arbitraria, sarà:
n = 2S / (a + c). Numero 7.
È lo stesso, ma con una linea di mezzo ben nota:
n = s / m. Sala 7a.
Stranamente, ma per un trapezio isoscele, le formule avranno lo stesso aspetto.
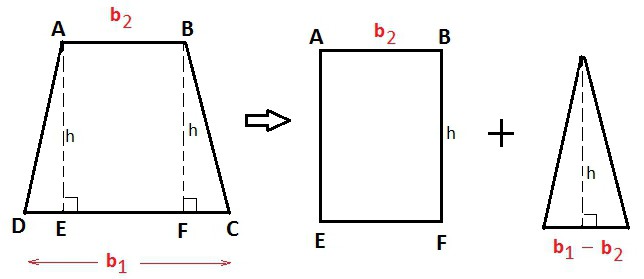
compiti
№1. Sulla definizione degli angoli nella parte inferiore del trapezio.
Condizioni. Viene dato un trapezio isoscele, il cui lato è di 5 cm. Le sue basi sono 6 e 12 cm. È necessario trovare il seno di un angolo acuto.
La decisione Per comodità, è necessario inserire la notazione. Lascia che il vertice in basso a sinistra sia A, tutto il resto in senso orario: B, C, D. Quindi, la base inferiore sarà contrassegnata HELL, la base superiore sarà BC.
Ad
È necessario disegnare altezze dai vertici B e C. Punti che indicano che le estremità delle altezze saranno designate rispettivamente come H 1 e H 2 . Poiché nella figura BCH 1 H 2 tutti gli angoli sono diritti, è un rettangolo. Ciò significa che il segmento H 1 H 2 è 6 cm.
Ora dobbiamo considerare due triangoli. Sono uguali perché sono rettangolari con ipotenusa identica e gambe verticali. Ne consegue che le loro gambe più piccole sono uguali. Pertanto, possono essere definiti come un quoziente della differenza. Quest'ultimo è ottenuto sottraendo dalla base inferiore di quella superiore. Sarà diviso per 2. Cioè, 12 - 6 deve essere diviso per 2. AN 1 = H 2 D = 3 (cm).
Ora dal teorema di Pitagora è necessario trovare l'altezza del trapezio. È necessario trovare il seno dell'angolo. BH 1 = √ (5 2 - 3 2 ) = 4 (cm).
Usando la conoscenza di come il seno di un angolo acuto si trova in un triangolo ad angolo retto, possiamo scrivere la seguente espressione: sin α = BH 1 / AB = 0.8.
La risposta è Il seno desiderato è 0.8.
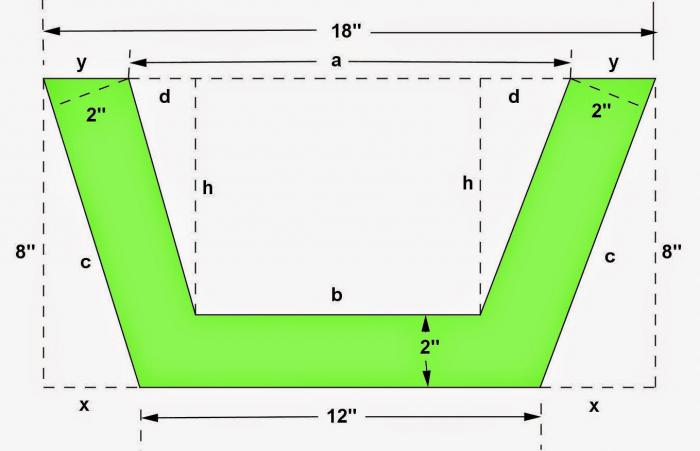
№2. Per trovare l'altezza del trapezio dalla famosa tangente.
Condizioni. Per un trapezio isoscele, è necessario calcolare l'altezza. Le sue basi sono note per essere 15 e 28 cm. Dan tangente di un angolo acuto: 11/13.
La decisione La designazione dei vertici è la stessa del compito precedente. Ancora una volta, è necessario tenere due altezze dagli angoli superiori. Per analogia con la soluzione del primo problema, è necessario trovare AH 1 = H 2 D, che sono definiti come la differenza 28 e 15 divisi per due. Dopo i calcoli risulta: 6,5 cm.
Ad
Poiché la tangente è il rapporto di due gambe, possiamo scrivere la seguente uguaglianza: tg α = AH 1 / BH 1 . Inoltre, questo rapporto è 11/13 (per condizione). Poiché AN 1 è noto, è possibile calcolare l'altezza: VN 1 = (11 * 6.5) / 13. I calcoli semplici danno un risultato di 5,5 cm.
La risposta è L'altezza richiesta è di 5,5 cm.
№3. Per calcolare l'altezza delle diagonali conosciute.
Condizioni. Si sa di un trapezio che le sue diagonali sono di 13 e 3 cm. È necessario conoscere la sua altezza se la somma delle basi è di 14 cm.
La decisione Lascia che la designazione della figura sia la stessa di prima. Supponiamo che l'altoparlante sia una diagonale più piccola. Dal vertice C è necessario mantenere l'altezza desiderata e designarla CH.
Ora è necessario eseguire ulteriori costruzioni. Dall'angolo C, devi disegnare una linea retta parallela alla diagonale più grande e trovare il punto della sua intersezione con la continuazione del lato della pressione sanguigna. Questo sarà D 1 . Si è scoperto un nuovo trapezio, all'interno del quale è disegnato il triangolo ASD 1 . È anche necessario per l'ulteriore soluzione del problema.
Ad
L'altezza desiderata sarà anche nel triangolo. Pertanto, è possibile utilizzare le formule studiate in un altro argomento. L'altezza di un triangolo è definita come il prodotto del numero 2 e l'area divisa per il lato a cui è disegnata. E il lato è uguale alla somma delle basi del trapezio originale. Questo si basa sulla regola che è stata eseguita la costruzione aggiuntiva.
Nel triangolo in esame, tutti i lati sono noti. Per comodità, introduciamo la notazione x = 3 cm, y = 13 cm, z = 14 cm.
Ora puoi contare l'area, usando il teorema di Gerona. Il semi-perimetro sarà p = (x + y + z) / 2 = (3 + 13 + 14) / 2 = 15 (cm). Quindi la formula per l'area dopo la sostituzione dei valori sarà simile a questa: S = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 √10 (cm 2 ).
Ora devi contare l'altezza: n = (2 * 6 √10) / 14 = 6√10 / 7 (cm).
La risposta è L'altezza è di 6√10 / 7 cm.
№4. Per cercare altezze ai lati.
Condizioni. Viene dato un trapezio, i tre lati dei quali sono di 10 cm e il quarto di 24 cm. Devi conoscere la sua altezza.
La decisione Dato che la figura è isoscele, allora avrai bisogno della formula numero 2. In essa hai solo bisogno di sostituire tutti i valori e contare. Sembrerà così:
n = √ (10 2 - (10 - 24) 2/4) = √51 (cm).
La risposta è n = √51 cm