Come trovare l'ipotenusa: 4 modi per trovare la risposta
Dopo aver studiato l'argomento triangoli rettangoli gli studenti spesso scartano tutte le informazioni su di loro. Compreso come trovare l'ipotenusa, per non parlare di cosa si tratta.

E invano. Perché più tardi la diagonale del rettangolo risulta essere questa ipotenusa, e deve essere trovata. o diametro di un cerchio coincide con il lato più grande del triangolo, uno dei cui angoli è dritto. E trovarlo senza questa conoscenza è impossibile.
Ci sono diverse opzioni per trovare l'ipotenusa di un triangolo. La scelta del metodo dipende dal set di dati iniziale nella dichiarazione dei valori del problema.
Metodo numero 1: entrambi sono indicati
Questo è il metodo più memorabile, perché utilizza il teorema di Pitagora. Solo a volte gli studenti dimenticano che questa formula è il quadrato dell'ipotenusa. Quindi, per trovare il lato stesso, dovrai estrarlo radice quadrata. Pertanto, la formula per l'ipotenusa, che di solito è indicata dalla lettera "c", sarà simile a questa:
Ad
c = √ (a 2 + in 2 ) , dove le due lettere del triangolo rettangolo sono scritte con le lettere "a" e "b".
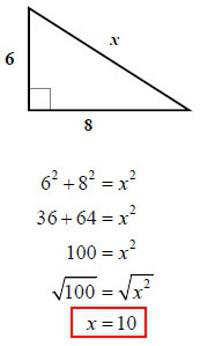
Metodo numero 2: noto per la gamba e l'angolo adiacente ad esso
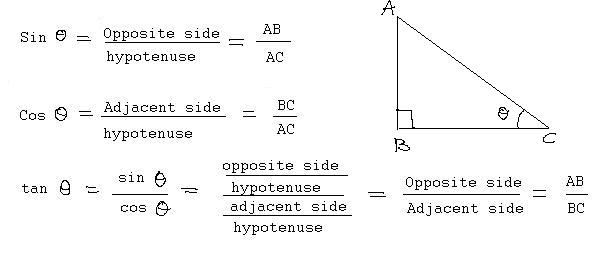
Per imparare come trovare l'ipotenusa, dovrai richiamare le funzioni trigonometriche. Vale a dire coseno. Per comodità, assumiamo che la gamba "a" e l'angolo ad esso adiacente siano dati.
Ora dobbiamo ricordare che il coseno dell'angolo di un triangolo rettangolo è uguale al rapporto tra i due lati. Il numeratore sarà il valore della gamba e il denominatore - l'ipotenusa. Da ciò ne consegue che quest'ultimo può essere contato dalla formula:
c = a / cos α .
Metodo numero 3: data la gamba e l'angolo che si trova di fronte a lui
Per non rimanere impigliati nelle formule, introduciamo la notazione per questo angolo - β, e lasciamo il lato della vecchia "a". In questo caso, è necessaria un'altra funzione trigonometrica, il seno.
Ad
Come nell'esempio precedente, il seno è uguale al rapporto tra la gamba e l'ipotenusa. La formula per questo metodo è la seguente:
c = a / sin β .
Per non rimanere impigliati nelle funzioni trigonometriche, puoi ricordare una semplice regola mnemonica: se il problema riguarda l' angolo opposto, devi usare s e nus, se si tratta di pr e mentire, quindi k sine. L'attenzione dovrebbe essere prestata alle prime vocali nelle parole chiave. Formano coppie o-e o -o .
Metodo numero 4: lungo la circonferenza del circumcircle
Ora, per imparare come trovare l'ipotenusa, dobbiamo richiamare la proprietà di un cerchio, che è descritto attorno a un triangolo rettangolo. Si legge come segue. Il centro del cerchio coincide con il centro dell'ipotenusa. Per dirla in altro modo, il lato più grande di un triangolo rettangolo è la diagonale di un cerchio. Cioè, il doppio del raggio. La formula per questa attività sarà simile a questa:
c = 2 * r , dove r è il raggio noto.
Questi sono tutti i modi possibili per trovare l'ipotenusa di un triangolo rettangolo. Per utilizzare in ciascuna attività specifica è necessario il metodo più adatto per un set di dati.
Esempio numero problema 1
Condizione: in un triangolo rettangolo, le mediane sono disegnate su entrambe le gambe. La lunghezza di quella trattenuta sul lato più grande è √52. L'altra mediana è lunga √73. Richiesto per calcolare l'ipotenusa.
Ad
La decisione
Poiché le mediane sono disegnate nel triangolo, dividono le gambe in due segmenti uguali. Per comodità, ragionamento e ricerca di come trovare l'ipotenusa, è necessario inserire alcuni simboli. Lascia che entrambe le metà del cateto più grande siano contrassegnate con la lettera "x" e l'altra con "y".
Ora dobbiamo considerare due triangoli rettangoli, i cui ipotenici sono mediani noti. Per loro è necessario scrivere due volte Formula del teorema di Pitagora :
(2y) 2 + x 2 = (√52) 2
e
(y) 2 + (2x) 2 = (√73) 2 .
Queste due equazioni formano un sistema con due incognite. Dopo averli risolti, sarà facile trovare le gambe del triangolo originale e la sua ipotenusa.
Per prima cosa devi costruire tutto al secondo grado. Si scopre:
4a 2 + x 2 = 52
e
a 2 + 4x 2 = 73.
Dalla seconda equazione si può vedere che 2 = 73 - 4x 2 . Questa espressione deve essere sostituita nella prima e calcolare "x":
4 (73 - 4x 2 ) + x 2 = 52.
Dopo la conversione:
292 - 16 x 2 + x 2 = 52 o 15x 2 = 240.
Dall'ultima espressione x = √16 = 4.
Ora puoi calcolare "y":
y 2 = 73 - 4 (4) 2 = 73 - 64 = 9.
y = 3.
A seconda della condizione, risulta che le gambe del triangolo originale sono 6 e 8. Pertanto, è possibile utilizzare la formula dal primo metodo e trovare l'ipotenusa:
√ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10.
Risposta : l'ipotenusa è 10.

Esempio numero di attività 2
Condizione: calcola la diagonale tracciata in un rettangolo con il lato più piccolo uguale a 41. Se è noto che divide l'angolo di quelli che si riferiscono come 2 a 1.
La decisione
In questa attività, la diagonale del rettangolo è il lato più grande del triangolo con un angolo di 90º. Pertanto, tutto si riduce a come trovare l'ipotenusa.
Il problema riguarda le curve. Ciò significa che dovrai utilizzare una delle formule in cui sono presenti funzioni trigonometriche. E prima devi determinare il valore di uno degli angoli acuti.
Ad
Lascia che il più piccolo degli angoli a cui si riferisce nella condizione sia α. Quindi l'angolo retto, che è diviso per la diagonale, sarà uguale a 3α. La notazione matematica per questo è:
90º = 3 α.
Da questa equazione, è sufficiente determinare α. Sarà uguale a 30º. E si troverà di fronte al lato più piccolo del rettangolo. Pertanto, avrai bisogno della formula descritta nel metodo numero 3.
L'ipotenusa è uguale al rapporto tra la gamba e il seno dell'angolo opposto, cioè:
41 / sin 30º = 41 / (0,5) = 82.
Risposta: l'ipotenusa è 82.