Come trovare la lunghezza dell'arco di un cerchio

La formula per trovare la lunghezza dell'arco di un cerchio è abbastanza semplice, e molto spesso su esami importanti come l'Esame di stato unificato ci sono problemi che non possono essere risolti senza la sua applicazione. Devi anche saperlo per superare test standardizzati internazionali, come il SAT e altri.

Qual è la lunghezza dell'arco di un cerchio?

La formula è la seguente:

l = πrα / 180 °

Qual è ciascuno degli elementi della formula:

• l è la lunghezza dell'arco di un cerchio;
• π è il numero pi (valore costante uguale a ≈ 3.14);
• r è il raggio di un dato cerchio;
• a è il valore dell'angolo su cui poggia l'arco (centrale piuttosto che inscritto).

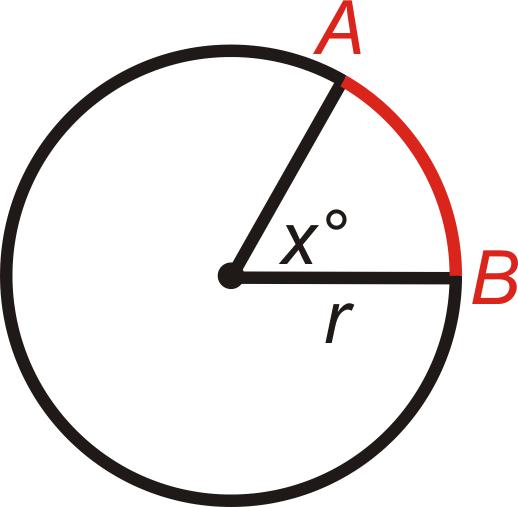
Come puoi vedere, per risolvere il problema, la condizione deve contenere r e α. Senza questi due valori, la lunghezza dell'arco non può essere trovata.

Come viene derivata questa formula e perché appare così?

Tutto è estremamente facile. Diventerà molto più chiaro se metti a 360 ° il denominatore e aggiungi un duce al numeratore in primo piano. Puoi anche α non partire in una frazione, ritirarlo e scrivere con un segno di moltiplicazione. È abbastanza possibile permettersi, dal momento che questo elemento è nel numeratore. Quindi la visione generale sarà:

l = (2πr / 360 °) × α

Solo per comodità, ridotto di 2 e 360 ​​°. E ora, se guardi da vicino, puoi notare una formula molto familiare per la lunghezza dell'intero cerchio, cioè 2πr. L'intero cerchio consiste di 360 °, perché dividiamo la misura ottenuta in 360 parti. Quindi moltiplichiamo per il numero α, cioè per il numero di "pezzi di torta" di cui abbiamo bisogno. Ma tutti sanno per certo che il numero (cioè la lunghezza dell'intero cerchio) non può essere diviso per gradi. Cosa fare in questo caso? Di solito, di regola, il grado si riduce con il grado dell'angolo centrale, cioè con α. Dopo tutto, rimangono solo i numeri e il risultato è la risposta finale.

Questo potrebbe spiegare perché la lunghezza dell'arco di un cerchio è in questo modo e ha questa forma.

Esempio di un problema di complessità media usando questa formula

Condizione: c'è un cerchio con un raggio di 10 centimetri. La misura in gradi dell'angolo centrale è 90 °. Trova la lunghezza dell'arco di un cerchio formato da questo angolo.

Soluzione: l = 10π × 90 ° / 180 ° = 10π × 1/2 = 5π

Risposta: l = 5π

È anche possibile che invece di una misura di laurea, venga data una misura dell'angolo radiante. In nessun caso non aver paura, perché questa volta il compito è diventato molto più facile. Per convertire un radiante in una misura di misura, è necessario moltiplicare questo numero di 180 ° / π. Quindi, ora puoi sostituire la seguente combinazione anziché α : m × 180 ° / π. Dove m è il valore radiante. E poi 180 e il numero π si riduce e si ottiene una formula completamente semplificata, che appare come segue:

l = mr,

dove:

• l è la lunghezza dell'arco di un cerchio;
• m è la misura radiante dell'angolo;
• r è il raggio di un dato cerchio.