Come trovare la radice quadrata? Proprietà, esempi di estrazione delle radici

La matematica nasce quando una persona si realizza e inizia a posizionarsi come unità autonoma del mondo. Il desiderio di misurare, confrontare, calcolare ciò che ti circonda - questa era la base di una delle scienze fondamentali dei nostri giorni. All'inizio, queste erano parti della matematica elementare, che ci permetteva di associare i numeri alle loro espressioni fisiche, le conclusioni successive furono presentate solo teoricamente (in virtù della loro astrattezza), beh, dopo qualche tempo, come disse uno scienziato, "la matematica raggiunse il limite della complessità quando scomparve tutti i numeri. " Il concetto di "radice quadrata" è apparso in un momento in cui poteva essere facilmente supportato da dati empirici, andando oltre il piano del calcolo.

Com'è cominciato tutto

La prima menzione della radice, che attualmente è indicata come √, fu registrata negli scritti dei matematici babilonesi, che iniziarono l'aritmetica moderna. Certo, assomigliavano un po 'alla forma attuale - gli scienziati di quegli anni in un primo momento usavano compresse voluminose. Ma nel secondo millennio aC. e. hanno derivato una formula di calcolo approssimativa che mostrava come estrarre la radice quadrata. La foto sotto mostra una pietra su cui gli scienziati babilonesi hanno scolpito il processo di √2, e si è rivelato essere così vero che la discrepanza nella risposta è stata trovata solo nel decimo decimale.

Inoltre, la radice veniva usata se era necessario trovare il lato del triangolo, a condizione che fossero noti gli altri due. Bene, al momento di decidere equazioni quadrate Dall'estrazione della radice non può andare da nessuna parte.

Insieme alle opere babilonesi, l'oggetto dell'articolo è stato anche studiato nell'opera cinese "Matematica in nove libri", e gli antichi greci giunsero alla conclusione che qualsiasi numero da cui nessuna radice viene estratta senza resto dà un risultato irrazionale.

L'origine di questo termine è associata alla rappresentazione araba del numero: gli antichi studiosi ritenevano che il quadrato di un numero arbitrario crescesse dalla radice, come una pianta. In latino, questa parola suona come radix (puoi tracciare il modello - tutto ciò che ha un significato di radice è consonante, sia esso ravanello o radicolite).

Gli scienziati di nuova generazione hanno raccolto questa idea, designandola come Rx. Ad esempio, nel XV secolo, per indicare che una radice quadrata viene estratta da un numero arbitrario a, hanno scritto R ² a. Il familiare "segno di spunta" √ apparve solo nel XVII secolo grazie a René Descartes.

I nostri giorni

Dal punto di vista della matematica, la radice quadrata di y è tale numero z, il cui quadrato è uguale a y. In altre parole, z ² = y è equivalente a √y = z. Tuttavia, questa definizione è rilevante solo per la radice aritmetica, poiché implica il valore non negativo dell'espressione. In altre parole, √y = z, dove z è maggiore o uguale a 0.

In generale, ciò che funziona per definire una radice algebrica, il valore di un'espressione può essere sia positivo che negativo. Quindi, a causa del fatto che z ² = y e (-z) ² = y, abbiamo: √y = ± z o √y = | z |.

A causa del fatto che l'amore per la matematica con lo sviluppo della scienza è solo aumentato, ci sono varie manifestazioni di affetto per esso, non espresse nel calcolo a secco. Ad esempio, alla pari di fenomeni divertenti come il giorno di Pi, si celebrano anche le festività della radice quadrata. Sono contrassegnati nove volte in cento anni e sono determinati secondo il seguente principio: i numeri, che indicano giorno e mese in ordine, devono essere la radice quadrata dell'anno. Quindi, la prossima volta festeggeremo questa festa il 4 aprile 2016.

Proprietà della radice quadrata sul campo R

1. La radice quadrata di un prodotto è uguale al prodotto di radici quadrate, a condizione che le espressioni radicali siano maggiori o uguali a 0.
2. Quando si erige una radice quadrata, è sufficiente elevare a questa potenza un'espressione radicale, a condizione che sia maggiore di zero.
3. La radice quadrata di una frazione è uguale alla radice del numeratore divisa per la radice del denominatore, a condizione che la radice quadrata del numeratore sia maggiore o uguale a 0 e la radice quadrata del denominatore sia strettamente maggiore di 0.
4. Un'espressione radicale, se è maggiore di zero, può essere divisa in più parti, da cui, a sua volta, è possibile estrarre la radice. Ad esempio: √75 = √25 * 3 = 5√3.
5. Sotto il segno della radice, puoi inserire qualsiasi numero, mentre lo si alza in un quadrato. Ad esempio: 5√8 = √25 * √8 = √200.

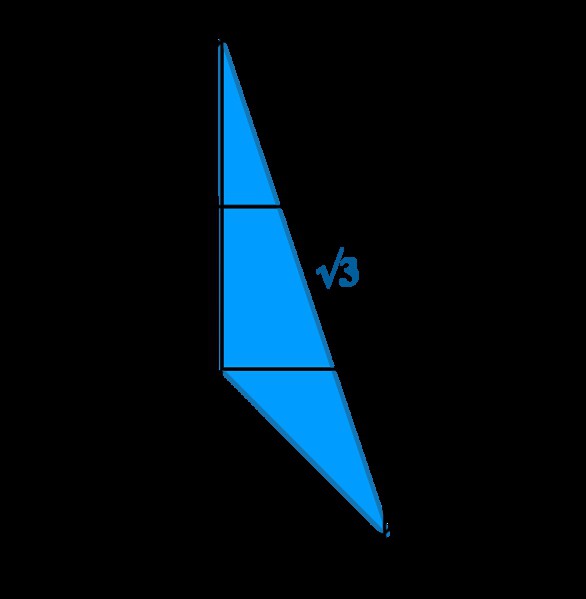
Praticamente tutte le espressioni matematiche hanno una base geometrica sotto di loro, questo destino e √y, che è definito come il lato di un quadrato con un'area di y, non è sfuggito.

Come trovare la radice di un numero?

Esistono diversi algoritmi per l'elaborazione. Il più semplice, ma piuttosto ingombrante, è il solito calcolo aritmetico, che consiste nel seguente:

1) dal numero di cui abbiamo bisogno la radice, vengono sottratti a turno numeri dispari - fino a quando il saldo dell'output non è deducibile o zero. Il numero di mosse e alla fine sarà il numero desiderato. Ad esempio, calcolando la radice quadrata di 25:

25-1 = 24

24-3 = 21

21-5 = 17

17-7 = 10

10-9 = 1

Il prossimo numero dispari è 11, il resto è il seguente: 1 <11. Il numero di mosse è 5, quindi la radice di 25 è 5. Tutto sembra facile e semplice, ma immagina cosa devi calcolare dal 18769? 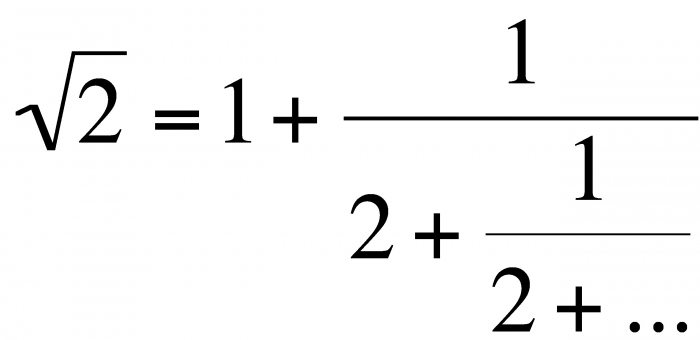Per questi casi, c'è una decomposizione nella serie di Taylor:

√ (1 + y) = Σ ((- 1) ⁿ (2n)! / (1-2n) (n!) ² (4 ⁿ )) y ⁿ , dove n prende valori da 0 a

+ ∞, e | y | ≤1.

Rappresentazione grafica della funzione z = √y

Si consideri una funzione elementare z = √y sul campo dei numeri reali R, dove y è maggiore o uguale a zero. Il suo programma è il seguente: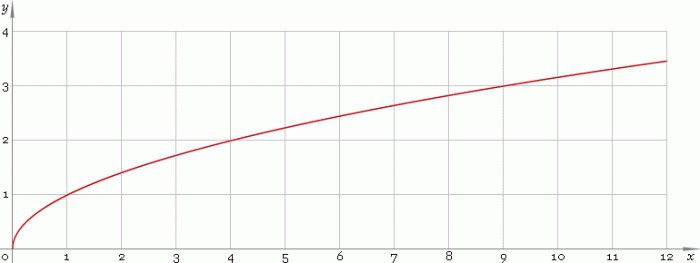

La curva cresce dall'origine e attraversa necessariamente il punto (1; 1).

Proprietà della funzione z = √y sul campo dei numeri reali R

1. Il dominio della funzione considerata è l'intervallo da zero a più infinito (lo zero è incluso).

2. L'intervallo di valori della funzione in questione è l'intervallo da zero a più infinito (lo zero è incluso di nuovo).

3. Il valore minimo di (0) la funzione accetta solo nel punto (0; 0). Il valore massimo è mancante.

4. La funzione z = √y non è né pari né dispari.

5. La funzione z = √y non è periodica.

6. Il punto di intersezione del grafico della funzione z = √y con gli assi delle coordinate è solo uno: (0; 0).

7. Il punto di intersezione del grafico della funzione z = √y è anche lo zero di questa funzione.

8. La funzione z = √y cresce continuamente.

9. La funzione z = √ prende solo valori positivi, quindi il suo grafico occupa il primo angolo di coordinate.

Varianti della funzione immagine z = √y

In matematica, per facilitare il calcolo di espressioni complesse, a volte viene utilizzata una forma di potere per scrivere la radice quadrata: √y = y ^1/2 . Tale opzione è conveniente, ad esempio, per aumentare una funzione alla potenza: (√y) ⁴ = (y ^1/2 ) ⁴ = y ² . Questo metodo è anche una buona idea per la differenziazione con l'integrazione, poiché a causa di esso la radice quadrata è rappresentata da una normale funzione di potenza.

E nella programmazione, la sostituzione del carattere √ è la combinazione di lettere sqrt. Va notato che in quest'area la radice quadrata è molto richiesta, in quanto fa parte della maggior parte delle formule geometriche necessarie per i calcoli. L'algoritmo di conteggio di per sé è piuttosto complesso ed è basato sulla ricorsione (una funzione che chiama se stessa).

Radice quadrata in campo complesso C

Nel complesso, è stato oggetto di questo articolo che ha stimolato l'apertura del campo. numeri complessi C, poiché i matematici non erano a proprio agio con la questione di ottenere una radice di grado pari da un numero negativo. Quindi, l'unità immaginaria che ho apparso, che è caratterizzata da una proprietà molto interessante: il suo quadrato è -1. Grazie a questo, le equazioni quadratiche e con una discriminante negativa hanno ottenuto una soluzione. In C, per la radice quadrata, sono rilevanti le stesse proprietà di R: l'unica cosa è che le restrizioni sul radicand vengono rimosse.